
En musique, une note est un symbole ou une lettre permettant de représenter un fragment de musique par une convention d'écriture de la hauteur et de la durée d'un son.
Anatomie du symbole

Le symbole visuel d'une note de musique sur une partition est constitué :
- d'une « tête » qui indique la hauteur du son (sa fréquence en hertz),
- d'une « hampe » qui soutient les crochets et les barres de durée,
- d'une « durée », matérialisée par un ou des crochets ou par une ou plusieurs barres horizontales ou inclinées, qui indique sa longueur ou durée temporelle.
La « tête » est généralement de forme ronde ovalisée et peut être évidée (ronde, blanche…) ou pleine (noire, croche…). Pour certains instruments, elle peut prendre diverses formes comme pour la percussion. Par exemple, le symbole :
La « hampe » est un trait vertical fin attaché à toutes les têtes de notes, sauf à la ronde. En règle générale, elle est placée au-dessus et à droite de la tête quand la tête de note est en dessous de la troisième ligne de la portée, et en dessous et à gauche quand la tête de note est sur ou au-dessus de la troisième ligne.
La « durée » des notes est matérialisée par un crochet simple ou des crochets multiples superposés, ou par une barre ou plusieurs barres épaisses parallèles, horizontales ou inclinées. L'assemblage des « durées » de notes constitue le rythme : à partir de la croche, le nombre de crochets (pour une note) ou de barres (pour un ensemble de notes) détermine la durée rythmique de la note : un pour la croche, deux pour la double-croche, trois pour la triple-croche, etc. Pour la ronde, la blanche et la noire, pointées ou non, qui n'ont pas de symbole de « durée » (crochet ou barres horizontales), la longueur de la note est donnée par le fait que la tête de note soit remplie ou pas, et/ou par le fait qu'elle ait une hampe ou pas.
Les notes, la partition et le solfège
L'assemblage des « têtes » de notes disposées à différentes hauteurs — qui donne la mélodie — et des « durées » de notes — qui donnent le rythme — forment la partition et le solfège, qui sont destinés à être lus et déchiffrés par le musicien interprète.
En plus de la hauteur et de la durée, les notes font l'objet d'autres effets acoustiques créés par la manière de jouer du musicien, comme d'une part, l'intensité ou nuance, indiquée sur la partition par des lettres placées à proximité des notes, comme ![]() pour piano,
pour piano, ![]() pour fortissimo, etc., et du phrasé musical d'autre part (attaques douces, attaques brutales, notes piquées, accents, etc.) indiqué par des symboles musicaux spécifiques (points, traits, chevrons, etc.). Enfin, une même note jouée par divers instruments, certes de même hauteur, se différencie également par son timbre, spécifique à chaque instrument (timbre doux pour la flûte, percutant pour le piano quand il est martelé, féerique pour le glockenspiel, puissant et cuivré pour la trompette, plus sourd pour le cor, etc.).
pour fortissimo, etc., et du phrasé musical d'autre part (attaques douces, attaques brutales, notes piquées, accents, etc.) indiqué par des symboles musicaux spécifiques (points, traits, chevrons, etc.). Enfin, une même note jouée par divers instruments, certes de même hauteur, se différencie également par son timbre, spécifique à chaque instrument (timbre doux pour la flûte, percutant pour le piano quand il est martelé, féerique pour le glockenspiel, puissant et cuivré pour la trompette, plus sourd pour le cor, etc.).
Des « têtes » de notes placées les unes après les autres, de gauche à droite, sont jouées successivement, ce qui forme une mélodie : chaque instrument d'un orchestre joue sa mélodie. Mais lorsque plusieurs « têtes » de notes sont superposées, elle doivent être jouées simultanément, ce qui crée un accord. C'est le cas pour un pianiste qui joue plusieurs notes en même temps avec une main, ou pour un ensemble instrumental où chaque musicien joue une des notes de l'accord.
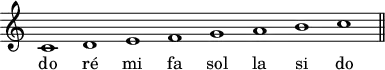
Fréquence d'une note - physique du son (acoustique)
Tout son musical (ou note) possède une fréquence fondamentale (nombre de vibrations par seconde calculé en hertz) correspondant à sa hauteur.
Tous les instruments de musique fonctionnent selon l'équation des cordes vibrantes, qui donne la fréquence du son joué en fonction des paramètres géométriques de construction de l'instrument (longueur de corde, diamètre de tuyau, etc.). Cette équation admet un ensemble de solutions de fréquences multiples de la fréquence dite fondamentale, qui correspond à la vibration du système vibrant (corde, tuyau, etc.).
Lorsqu'un son donné de fréquence est joué, l'ensemble des fréquences , , , , etc., sont également émises par l'instrument. La note correspondant à la fréquence est appelée fondamentale, et les autres sont ses harmoniques. L'ensemble de ces fréquences, associées à leur intensité (c'est-à-dire si on les entend fort ou non) est appelé spectre, ou plus communément timbre.
Dans un son de fondamentale , les harmoniques les plus présentes sont l'octave (), la quinte (), l'octave (), la tierce majeure (), etc.[1].
Deux notes dont les fréquences fondamentales ont un rapport qui est une puissance de deux (c'est-à-dire la moitié, le double, le quadruple…) donnent deux sons très similaires et portent le même nom. Cette observation permet de regrouper toutes les notes qui ont cette propriété dans la même catégorie de hauteur.
Dans la musique occidentale, douze fréquences fondamentales différentes portent un nom. Sept d'entre elles sont considérées comme les principales et ont pour noms : do, ré, mi, fa, sol, la et si. Elles correspondent aux harmoniques naturels lorsque la note do est jouée.
Les cinq notes restantes sont dites « altérations » et sont des notes intermédiaires. Par exemple, la ![]() est une note de fréquence intermédiaire entre le la et le si.
est une note de fréquence intermédiaire entre le la et le si.
Pour distinguer deux notes de même nom dans deux octaves différentes, on numérote les octaves et donne ce numéro aux notes correspondantes : par exemple, le la3 a une fréquence de 440 hertz définie dans la norme internationale ISO 16[2] (bien qu'en pratique, cela puisse parfois varier). Cette fréquence de référence est donnée par un diapason.
Depuis le XVIIe siècle, on considère que les notes sont également réparties sur une octave, c'est-à-dire que le rapport de fréquences entre une note et la suivante est de (exemple : la3 = 440 Hz ; la ![]() 3 = 466,16 Hz).
3 = 466,16 Hz).
La définition de l'écart entre les notes est ce que l'on appelle le tempérament, et lorsque l'écart entre une note et la suivante (en termes de fréquences) est toujours identique, ce tempérament est dit « égal ».
Dans la gamme tempérée, la formule permettant de mesurer la fréquence d'une note par rapport à une note de départ est : . Avec le nombre de demi-tons au-dessus de la note de départ . On s'aperçoit que la fréquence croît de manière géométrique par rapport à la note.
De ce fait, chaque demi-ton correspond à une augmentation / diminution de la fréquence suivant un rapport de 1,0594630943 : 1 de la note voisine.
Néanmoins, le tempérament égal a ses limites : lorsqu'une note est jouée, les harmoniques 3 et 5 (la quinte et la tierce) sont audibles, et leur fréquence est de et de .
Par exemple, pour un la3 (440 Hz), on entend également la quinte (1 320 Hz) et la tierce majeure (2 200 Hz). Cette quinte et cette tierce se retrouvent également à la moitié ou le quart de leur fréquence (une octave en dessous) : 660 Hz (mi4) et 550 Hz (do ![]() 4).
4).
Or, dans la gamme tempérée (à tempérament égal), le mi étant la quinte du la, elle est séparée du la d'un facteur , c'est-à-dire que le mi4 a sa fondamentale à 659,25 Hz, et le do ![]() 4 a sa fondamentale à 554,37 Hz.
4 a sa fondamentale à 554,37 Hz.
On remarque alors que si on joue une tierce harmonique (la4 et do ![]() 4 simultanément par exemple) avec un tempérament égal, l'harmonique de tierce de la fondamentale et la fréquence fondamentale de la tierce ne sont pas à la même fréquence.
4 simultanément par exemple) avec un tempérament égal, l'harmonique de tierce de la fondamentale et la fréquence fondamentale de la tierce ne sont pas à la même fréquence.
| Note/octave | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| do ou si |
16,35 | 32,70 | 65,41 | 130,81 | 261,63 | 523,25 | 1046,50 | 2093,00 | 4186,01 | 8 372,02 | 16 744,04 |
| do |
17,33 | 34,65 | 69,30 | 138,59 | 277,18 | 554,37 | 1108,73 | 2217,46 | 4434,92 | 8 869,84 | 17 739,68 |
| ré | 18,36 | 36,71 | 73,42 | 146,83 | 293,66 | 587,33 | 1174,66 | 2349,32 | 4698,64 | 9 397,28 | 18 794,56 |
| ré |
19,45 | 38,89 | 77,78 | 155,56 | 311,13 | 622,25 | 1244,51 | 2489,02 | 4978,03 | 9 956,06 | 19 912,12 |
| mi ou fa |
20,60 | 41,20 | 82,41 | 164,81 | 329,63 | 659,26 | 1318,51 | 2637,02 | 5274,04 | 10 548,08 | 21 096,16 |
| fa ou mi |
21,83 | 43,65 | 87,31 | 174,61 | 349,23 | 698,46 | 1396,91 | 2793,83 | 5587,65 | 11 175,30 | 22 350,60 |
| fa |
23,13 | 46,25 | 92,50 | 185,00 | 369,99 | 739,99 | 1479,98 | 2959,96 | 5919,91 | 11 839,82 | 23 679,64 |
| sol | 24,50 | 49,00 | 98,00 | 196,00 | 392,00 | 783,99 | 1567,98 | 3135,96 | 6271,93 | 12 543,86 | 25 087,72 |
| sol |
25,96 | 51,91 | 103,83 | 207,65 | 415,30 | 830,61 | 1661,22 | 3322,44 | 6644,88 | 13 289,76 | 26 579,52 |
| la | 27,50 | 55,00 | 110,00 | 220,00 | 440,00 | 880,00 | 1760,00 | 3520,00 | 7040,00 | 14 080,00 | 28 160,00 |
| la |
29,14 | 58,27 | 116,54 | 233,08 | 466,16 | 932,33 | 1864,66 | 3729,31 | 7458,62 | 14 917,24 | 29 834,48 |
| si ou do |
30,87 | 61,74 | 123,47 | 246,94 | 493,88 | 987,77 | 1975,53 | 3951,07 | 7902,13 | 15 804,26 | 31 608,52 |
Degré et échelles musicales

Dans la théorie de la musique, on parle de « degré ». Celui-ci représente une hauteur relative appartenant à une échelle musicale donnée. En effet, il existe de nombreuses possibilités pour choisir les fréquences des notes dans une octave. Le choix des échelles dépend des époques, des instruments et des types de musique.
Selon l'échelle, on obtiendra des gammes musicales différentes. La musique classique en utilise deux : l'échelle diatonique et l'échelle chromatique.
Noms des notes de musique
Pour nommer les notes de musique, la musique occidentale utilise deux systèmes différents, selon le pays :
- le premier système, inspiré de l'Antiquité, utilise les premières lettres de l'alphabet. Il est en vigueur, dans deux variantes simplifiées (ne différant que par la désignation du si), dans les pays anglophones et germanophones ;
- le second système utilise les syllabes d'un chant latin. Il a été élaboré pendant la deuxième moitié du Moyen Âge et il est en usage en France, en Italie, etc.
| Allemagne
et pays germanophones |
Angleterre
et pays anglophones |
Langues latines
et slaves |
|---|---|---|
| C | C | do et ut |
| D | D | ré |
| E | E | mi |
| F | F | fa |
| G | G | sol |
| A | A | la |
| H | B | si |
Histoire
Depuis Guido d'Arezzo, les notes de musique peuvent être désignées par ut, ré, mi, fa, sol, la. Cette pratique a été standardisée par les recommandations du pape Jean XIX. Auparavant, en Occident, divers systèmes de notation existaient. La nouvelle méthode permettait d'apprendre en un jour ce qu'il fallait un an pour apprendre avec la méthode grecque utilisant des lettres pour noter tant les tons que les échelles[3].
La série constituée des syllabes ut, ré, mi, fa, sol, la (le si a été ajouté plus tard), promue par le moine bénédictin italien Guido d'Arezzo au XIe siècle, a été mise en place pour la notation musicale dans les pays de rite catholique dit « latin ». Cette série est constituée des premières syllabes de chaque demi-vers de l’Hymne à saint Jean-Baptiste, un chant religieux latin attribué au moine et érudit Paul Diacre :
« Ut queant laxis
Resonare fibris
Mira gestorum
Famuli tuorum
Solve polluti
Labii reatum
Sancte Iohannes »
L’ut, renommé do, est surtout utilisé dans le langage théorique[4] : clés, tonalités…
La septième note si fut ainsi dénommée à partir des initiales de Sancte Ioannes dans le dernier vers. C'est plus tard, en Italie, que le nom ut, seule note de la gamme sans consonne en son début pour marquer l'attaque de celle-ci, a été remplacé par la syllabe do, à la diction plus aisée. Son origine exacte reste inconnue, mais do pourrait être la première syllabe de Domine : Seigneur, donc Dieu, en latin. En outre, selon certains, cette syllabe ouverte contrairement au ut fermé, serait plus facile à émettre, pour les besoins du déchiffrage chanté de musiques sans paroles, dans l'apprentissage du solfège. Depuis lors, on parle de la note do (ou do bémol, do dièse, do bécarre, etc.), mais on évoque toujours la clé d'ut. Quant aux tonalités, les deux noms coexistent : ut majeur ou do majeur, ut mineur ou do mineur, etc.
Symbolique
En général, la musique est souvent représentée par une ou des notes, que ce soit dans la bande dessinée, pour symboliser un chant, ou dans l'informatique, pour spécifier que le fichier est un fichier musical.
Codage informatique
La représentation des symboles musicaux en informatique existe dans différents jeux de caractère (Unicode, LaTeX, LilyPond…). Par exemple, l'encodage en Unicode, pour ♩ (une noire), ♪ (une croche), ♫ (deux croches) et ♬ (deux doubles-croches) :
| Code HTML | Unicode | Rendu |
|---|---|---|
| ♩ | U+2669 | ♩ |
| ♪ | U+266A | ♪ |
| ♫ | U+266B | ♫ |
| ♬ | U+266C | ♬ |
Il existe également des notes dans la table des emojis.
| Unicode | Rendu |
|---|---|
| U+1f3b5 | 🎵 |
| U+1f3b6 | 🎶 |
Cependant, cet encodage ne permet pas le positionnement sur la portée, ni aucune autre manière de distinguer les hauteurs de son. Pour cela, on emploie d'autres normes. Par exemple, un des aspects de la norme MIDI est la numérotation des notes. On dit alors que le la 440 Hz est le numéro 69 et que toute différence de numéro par rapport à cette note est comptée en demi-tons. Par exemple, tous les multiples de 12 sont des do. À l'origine, seuls les numéros de 0 à 127 étaient permis, mais selon la variante de cette échelle, des notes plus graves ou plus aiguës peuvent aussi être permises. À partir du moment où on suppose un tempérament égal (gamme tempérée), on peut aussi représenter des notes intermédiaires en utilisant des fractions (voir la formule de fréquence mentionnée ci-haut).
D'autres notations informatisées utilisent les lettres de notes anglaises de A à G et le symbole # tenant lieu de dièse, mais pas de symbole bémol car non-nécessaire (tout bémol a un équivalent dièse). Les notes non-dièse peuvent être suivies d'un trait d'union ou d'une espace. On termine ensuite avec le numéro d'octave, qui augmente de 1 à chaque do comme dans la table ci-haut, mais qui peuvent être décalés (le la 440 pourrait être écrit A-2, A-3 ou A-4 selon l'échelle choisie). C'est ce qui est utilisé visuellement dans les éditeurs de type tracker (à la Amiga), quoique à l'interne, leurs formats utilisent des périodes (inverses de fréquences) comme le format MOD, ou une combinaison note de la gamme et octave (par exemple, les deux parties de la division avec reste d'une note MIDI par 12) comme le format S3M.
Notes et références
- ↑ Jean-Louis Fabre, L'écriture tonale : cours et méthode, dl 2018 (ISBN 978-2-9556093-2-3 et 2-9556093-2-3, OCLC 1089725516, lire en ligne).
- ↑ ISO 16:1975 Acoustique — Fréquence d'accord normale (Fréquence musicale normale), ISO, (lire en ligne).
- ↑ Antoine Furetière, Dictionnaire universel, contenant généralement tous les mots françois tant vieux que modernes, & les termes des sciences et des arts, vol. 2, La Haye / Rotterdam, Arnoud et Reinier Leers (en), , 2e éd. (lire en ligne sur Gallica).
- ↑ Marc Vignal (dir.), Dictionnaire de la musique, Encyclopédie Larousse, (lire en ligne), « Ut queant laxis », p. 1010.
Voir aussi
Bibliographie
- Adolphe Danhauser, Théorie de la musique : Édition revue et corrigée par Henri Rabaud, Paris, Éditions Henry Lemoine, , 128 p. (ISMN 979-0-2309-2226-5).
- Claude Abromont et Eugène de Montalembert, Guide de la théorie de la musique, Librairie Arthème Fayard et Éditions Henry Lemoine, coll. « Les indispensables de la musique », , 608 p. [détail des éditions] (ISBN 978-2-213-60977-5).
Articles connexes
- Acoustique musicale
- Désignation des notes de musique suivant la langue
- Histoire de la notation musicale
Liens externes
- Notices dans des dictionnaires ou encyclopédies généralistes :





![{\sqrt[ {12}]{2}}](https://img.franco.wiki/i/bc835f27425fb3140e1f75a5faa35b1e8b9efc35.svg)


