En mathématiques, une représentation paramétrique ou paramétrage d’un ensemble est sa description comme ensemble image d’une fonction d’une ou plusieurs variables appelées alors paramètres. Pour un ensemble de points du plan ou d’un espace de plus grande dimension muni d’un repère, l’expression des différentes composantes se décompose en contraintes sur le paramétrage appelées équations paramétriques.

En particulier, elle peut définir un chemin ou un ensemble géométrique ; comme une courbe ou une surface. Elle est importante en cinématique ; le paramètre est alors généralement le temps.

Cette représentation est duale de la description de l’ensemble par des équations cartésiennes.

Arc paramétré

Un exemple de dessin défini par différentes courbes paramétrées planes (courbes du papillon).

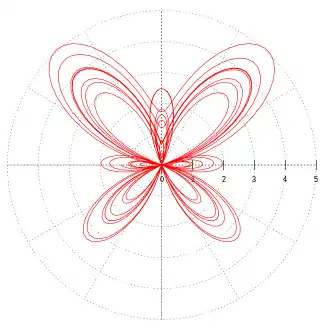
Pour donner corps au concept général et vague de courbe, on introduit une notion plus concrète d’arc paramétré.

Paramétrisation d’une droite (exemple)

L'objectif est de définir une droite Δ dans un espace euclidien. Soit ${\displaystyle {\mathcal {A}}}$ un espace affine réel de dimension 3, E son espace vectoriel associé et (O, e₁, e₂, e₃) un repère orthonormal R de E. On suppose que la droite Δ contient le point A de coordonnées (1 ; 3 ; 5) et qu'elle possède u, de coordonnées (2 ; -3 ; 5) dans la base associée au repère R, comme vecteur directeur^[1].

Soit un point M élément de la droite Δ, le vecteur d'extrémité A et M est colinéaire à u, car u est un vecteur directeur de Δ, cela signifie qu'il existe un nombre réel k tel que :

${\displaystyle {\overrightarrow {AM}}=k{\vec {u}}\quad {\text{et}}\quad {\overrightarrow {AM}}=2k{\vec {e_{1}}}-3k{\vec {e_{2}}}+5k{\vec {e_{3}}}}$

Cette égalité s'écrit encore, en fonction de coordonnées, si x, y et z désignent les coordonnées du point M dans le repère R :

${\displaystyle {\begin{pmatrix}x-1\\y-3\\z-5\end{pmatrix}}={\begin{pmatrix}2k\\-3k\\5k\end{pmatrix}}}$

Les coordonnées d'un point M de la droite Δ vérifient les égalités suivantes, dites équation paramétrique de la droite :

${\displaystyle (\Delta )\quad \left\{{\begin{matrix}x&=&{\color {Blue}2}k&+&{\color {Red}1}\\y&=&{\color {Blue}-3}k&+&{\color {Red}3}\\z&=&{\color {Blue}5}k&+&{\color {Red}5}\end{matrix}}\right.}$

On remarque que les valeurs bleues correspondent aux coordonnées du vecteur directeur u et les rouges au point A.

Hélice (exemple)

L'exemple introductif montre comment il est possible de définir un ensemble géométrique de l'espace à l'aide d'une équation paramétrée d'une droite. Cette propriété ne se limite pas à une droite, un arc paramétrique se définit aussi à l'aide d'une équation de cette nature. Ainsi, une hélice est définie par une équation du type^[2] :

${\displaystyle \left\{{\begin{matrix}x=&x_{0}+&r\cdot \cos(2\pi \cdot t)\\y=&y_{0}+&r\cdot \sin(2\pi \cdot t)\\z=&z_{0}+&p\cdot t\end{matrix}}\right.\quad {\text{avec}}\quad r,p\in \mathbb {R} }$

Nappe paramétrée

Un cône de révolution, exemple de nappe paramétrée.

La surface est un objet qui peut s’étudier en ayant recours à deux paramètres simultanément : on obtient alors une nappe paramétrée, pour laquelle la donnée de u et de v détermine un point M(u, v). Si on ne fait varier qu'un des deux paramètres, l'autre restant à une valeur fixe, on obtient un arc paramétré. Une nappe paramétrée peut en fait se concevoir comme formée d'une sorte de « grillage » dont les fils sont des arcs paramétrés.

Une nappe paramétrée de classe ${\displaystyle {\mathcal {C}}^{k}}$ dans l’espace vectoriel E de dimension finie est la donnée d’un domaine U (en général supposé connexe) de ℝ² où variera le couple de paramètres réels (t, u) et d’une fonction f de U dans E, de classe ${\displaystyle {\mathcal {C}}^{k}}$

Par exemple voici un paramétrage d'un cône de révolution de l'espace (parcouru plusieurs fois) : x(t, u)=u* cos (t), y(t, u)=u*sin(t), z(t, u)=u pour t, u variant dans ℝ.

Généralisation à p paramètres

Le nombre de paramètres est lié à la notion de dimension de l'objet géométrique, généralisant le concept de dimension de l'algèbre linéaire. La définition formelle des paramétrages, changements de paramètres, fait intervenir le calcul différentiel dont l'objectif de la géométrie différentielle est de recenser un certain nombre de notions et grandeurs qui sont invariantes par changement de paramètres. Dans le cas d'un arc paramétré, par exemple, on dira qu'une telle notion ou grandeur relève non plus seulement de l'arc paramétré mais d'un objet mathématique nouveau, l’arc (ou la courbe) géométrique.

L'extension à p paramètres permet de formaliser la notion de variété de dimension p tracée dans un espace E de dimension n. On reprend, mutatis mutandis, les définitions de la dimension 2 :

• quand l'application f a une différentielle injective (f est une immersion), on dit que la variété est immergée dans E. Ceci généralise la notion d'arc régulier, de nappe régulière. Et on peut alors définir le sous-espace tangent ;
• il faut des contraintes supplémentaires pour que cette immersion devienne un plongement, permettant de parler de sous-variété de E.

Et de la même façon, il y a une notion de changement de paramétrage par difféomorphisme qui conserve les notions d'immersion, de sous-espace tangent.

Hypersurface

Dans un espace euclidien, il est possible de paramétrer une hypersurface de dimension quelconque.

Les équations suivantes correspondent à celles d'une surface cylindrique de révolution C, plongée dans un espace affine de dimension 3.

${\displaystyle (C)\quad \left\{{\begin{matrix}x&=&a_{1}&+&r\cdot \cos(2\pi \cdot k_{1})\\y&=&a_{2}&+&r\cdot \sin(2\pi \cdot k_{1})\\z&=&0&+&k_{2}\end{matrix}}\right.}$

Sous-espace affine

Tout espace vectoriel ou sous-espace affine de dimension finie admet une représentation paramétrique linéaire ou affine avec un nombre de paramètres égal à sa dimension, grâce à une base ou un repère. Une courbe (une dimension) ou une surface (deux dimensions) régulière peut admettre différentes paramétrisations.

Si maintenant A est un espace affine de dimension n, d'espace vectoriel associé E si (O, e₁, …, e_n) est un repère R de A, il est aussi possible de définir un sous-espace affine S de A à l'aide d'un système d'équations paramétriques. Soit d la dimension du sous-espace affine contenant un point M de coordonnées (a₁, …, a_n) et de direction de base (u₁, …, u_d). Soit (u_j1, …, u_jn) les coordonnées du vecteur u_j, j = 1, …, d; l'équation paramétrique du sous-espace affine S a pour coordonnées^[3] :

${\displaystyle (S)\quad \left\{{\begin{matrix}x_{1}&=&a_{1}&+&k_{1}u_{11}+\cdots +k_{d}u_{d1}\\x_{2}&=&a_{2}&+&k_{1}u_{12}+\cdots +k_{d}u_{d2}\\\vdots \\x_{n}&=&a_{n}&+&k_{1}u_{1n}+\cdots +k_{d}u_{dn}\end{matrix}}\right.}$

En cinématique

Un exemple de mouvement de point en fonction du temps.

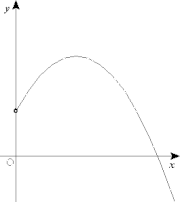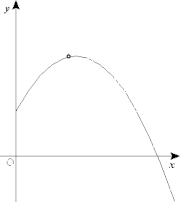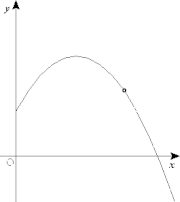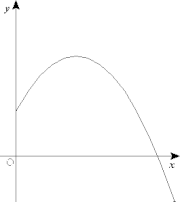
On étudie la succession des points de l'espace animés d'un mouvement dont on connaît la loi en fonction du temps. Ainsi la donnée d'une valeur du temps t permet la détermination de la position M(t) au temps t.

Il peut être judicieux de décrire ce même mouvement en changeant de paramètre de référence, en remplaçant par exemple le temps t par l’abscisse curviligne s.

Voir aussi

• Équation cartésienne
• Géométrie différentielle classique
• Variété
• Cinématique

Références

• Cet article est partiellement ou en totalité issu de l'article intitulé « Paramétrage » (voir la liste des auteurs).
• Cet article est partiellement ou en totalité issu de l'article intitulé « Équation paramétrique » (voir la liste des auteurs).