L'unité arithmétique et logique (UAL, en anglais arithmetic–logic unit, ALU), est l'organe de l'ordinateur chargé d'effectuer les calculs. Le plus souvent, l'UAL est incluse dans l'unité centrale de traitement ou le microprocesseur. Elle est constituée d'un circuit à portes logiques.
Différents types d'UAL
Les UAL peuvent être spécialisées ou pas. Les UAL élémentaires calculent sur des nombres entiers, et peuvent effectuer les opérations communes, que l'on peut séparer en quatre groupes :
- Les opérations arithmétiques : addition, soustraction, changement de signe, etc.
- les opérations logiques bit à bit : compléments à un, à deux, et, ou, ou exclusif, non, non-et, etc.
- les comparaisons : test d'égalité, supérieur, inférieur, et leur équivalents « ou égal ».
- éventuellement des décalages et rotations (mais parfois ces opérations sont externalisées).
Certaines UAL sont spécialisées dans la manipulation des nombres à virgule flottante, en simple ou double précision (on parle d'unité de calcul en virgule flottante (UVF, en anglais floating-point unit, FPU) ou dans les calculs vectoriels. Typiquement, ces unités savent accomplir les opérations suivantes :
- addition, soustraction, changement de signe ;
- multiplication, division, racine carrée ;
- comparaisons ;
- modulo.
Certaines UAL, le plus souvent de la classe des FPUs, notamment celles des superordinateurs, sont susceptibles d'offrir des fonctions avancées :
- fonctions transcendantes (sin x, cos x, etc.) ;
- opérations vectorielles (produit scalaire, vectoriel, etc.) ;
- etc.
Les processeurs modernes font appel à plusieurs UAL, au moins deux : une située dans le chemin de contrôle pour incrémenter le compteur ordinal (de 1, 2, 4 ou 8 typiquement), et une autre dans le chemin de données pour traiter l'information. Pour augmenter leurs performances, elles sont le plus souvent pipelinées.
Notation

La figure ci-contre représente un schéma classique d'UAL. Celle-ci possède deux entrées A et B sur lesquelles on présente les données à traiter. L'entrée F désigne l'opération à effectuer.
Enfin, l'UAL possède deux sorties, R qui est le résultat de l'opération, et D les éventuels drapeaux.
Drapeaux (D)
Il existe différents drapeaux[1] qui définissent ou une erreur dans le résultat (division par zéro, dépassement de mémoire...), ou alors des codes conditions (supérieur, inférieur, égal à zéro...).
La plupart des UAL possèdent des drapeaux qui ont différentes significations, dont voici plusieurs exemples :
- Report (en : Carry-out), transporte le report résultant d'une addition, la retenue résultant d'une opération de soustraction, ou le bit de dépassement résultant d'une opération de décalage binaire.
- Zéro, indique que tous les bits de R sont égaux à zéro.
- Négatif, indique que le résultat de l'opération arithmétique est négatif.
- Débordement (en anglais : overflow), indique que le résultat d'une opération arithmétique a excédé la capacité numérique de R.
Exemples
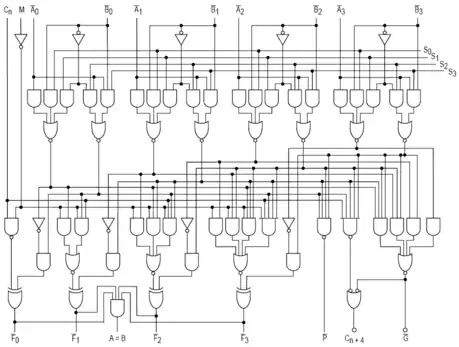
L'UAL 4 bits 74181 (TTL)
Voici, par exemple, une UAL qui fut très utilisée au moment où seuls les circuits intégrés TTL étaient disponibles : le 74181, une UAL de 4 bits. Ce circuit est destiné à être connecté en cascade avec d'autres pour traiter des entiers de taille supérieure à 4 bits. Il est à la base des UAL de l'Alto et dans de nombreux modèles de PDP-11 (16 bits).
Sa table de vérité décrivant quelle opération est accomplie suivant les valeurs des entrées M et S.
| Fonction | M = 1 | M = 0 | ||||
|---|---|---|---|---|---|---|
| S3 | S2 | S1 | S0 | Opération logique | Cn = 0 | Cn = 1 |
| 0 | 0 | 0 | 0 | F = non A | F = A | F = A + 1 |
| 0 | 0 | 0 | 1 | F = non (A ou B) | F = A ou B | F = (A ou B) + 1 |
| 0 | 0 | 1 | 0 | F = (non A) et B | F = A ou (non B) | F = (A ou (non B)) + 1 |
| 0 | 0 | 1 | 1 | F = 0 | F = - 1 | F = 0 |
| 0 | 1 | 0 | 0 | F = non (A et B) | F = A + (A et (non B)) | F = A + (A et (non B)) + 1 |
| 0 | 1 | 0 | 1 | F = non B | F = (A ou B) + (A et (non B)) | F = (A ou B) + (A et(non B)) + 1 |
| 0 | 1 | 1 | 0 | F = A xor B | F = A - B - 1 | F = A - B |
| 0 | 1 | 1 | 1 | F = A et (non B) | F = (A et (non B)) - 1 | F = A et (non B) |
| 1 | 0 | 0 | 0 | F = (non A) ou B | F = A + (A et B) | F = (A + (A et B)) + 1 |
| 1 | 0 | 0 | 1 | F = non (A xor B) | F = A + B | F = A + B + 1 |
| 1 | 0 | 1 | 0 | F = B | F = (A ou (non B)) + (A et B) | F = A ou (non B) + (A et B) + 1 |
| 1 | 0 | 1 | 1 | F = A et B | F = (A et B) - 1 | F = A et B |
| 1 | 1 | 0 | 0 | F = 1 | F = A + (A << 1) | F = A + A + 1 |
| 1 | 1 | 0 | 1 | F = A ou (non B) | F = (A ou B) + A | F = (A ou B) + A + 1 |
| 1 | 1 | 1 | 0 | F = A ou B | F = (A ou (non B)) + A | F = A (non B) plus A plus 1 |
| 1 | 1 | 1 | 1 | F = A | F = A - 1 | F = A |
Attention : ce tableau peut contenir des erreurs.
Le schéma de ce circuit est donné ci-dessous.
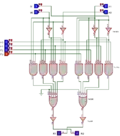
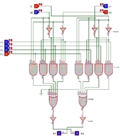
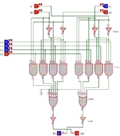
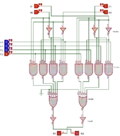
Utilisation de multiplexeurs 4 vers 1 comme UAL
La technique des multiplexeurs est utilisée dans l'UAL de l'IBM 7030 « Stretch » (1961). Le concept repose sur le choix judicieux du code fonction F : il correspond aussi au résultat de l'opération désirée. Par exemple, pour faire un ET, on choisira le code F = 0001, correspondant à la colonne de résultat de la table de vérité du et logique. De même, pour un ou on prend F = 0111, pour un ou exclusif F = 0110, etc.
| A | B | A ET B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Pour chaque couple de bits à traiter , on construit les quatre signaux , , et . Ces signaux sont envoyés en entrée d'un multiplexeur, dont l'entrée est F. Cela revient donc à appliquer la fonction logique en question.
L'exemple ci-dessous présente un tel multiplexeur sur deux bits. Le premier multiplexeur prend, comme entrée, les deux bits de poids faible de A et B. Ils servent à sélectionner une des lignes de F : 00 sélectionnera la première ligne, 01 la seconde et ainsi de suite. Le second multiplexeur agit de la même façon avec les deux bits de poids fort de A et B :
 00 ET 00 = 00 |
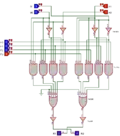 00 ET 11 = 00 |
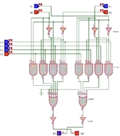 01 ET 01 = 01 |
 10 ET 01 = 00 |
 11 ET 01 = 01 |
 11 ET 11 = 11 |
Le schéma des multiplexeurs 4 vers 1 ci-dessus est construit à base de circuits intégrés TTL tout à fait standard, dont les références sont affichées. Il s'agit de portes NON, ET et NON-OU.
Voir aussi
- Bit
- Algèbre de Boole
- Informatique
- Liste de microprocesseurs
- Microprocesseur
Références
- ↑ « DSCPU ALU », sur personal.denison.edu (consulté le )




