فرضية الخط المتعرج

فرضية الخط المتعرج في الرياضيات ، ولا سيما الجبر التماثلي، هي التي تؤكد وجود تسلسل طويل محدد بمجموعات تماثل مركبات متسلسلة بعينها، والنتيجة صالحة في كل زمرة أبيلية .

البرهان

في أي صيغة أبيلية (كصيغة المجموعات الأبيلية أو فئة الفضاءات المتجهة على حقل محدد) ، اجعل ${\displaystyle ({\mathcal {A}},\partial _{\bullet }),({\mathcal {B}},\partial _{\bullet }')}$ ،${\displaystyle ({\mathcal {C}},\partial _{\bullet }'')}$ مركبات متسلسلة تناسب المتتالية القصيرة التحديدية الآتية:

${\displaystyle 0\longrightarrow {\mathcal {A}}{\stackrel {\alpha }{\longrightarrow }}{\mathcal {B}}{\stackrel {\beta }{\longrightarrow }}{\mathcal {C}}\longrightarrow 0}$

ومثل هذا التسلسل مختصر للمخطط التبادلي الآتي:

على اعتبار الصفوف متتاليات منضبطة وكل عامود مركبًا تسلسليًّا. تفترض فرضية الخط المتعرج أن هناك مجموعة من خرائط الحدود:

${\displaystyle \delta _{n}:H_{n}({\mathcal {C}})\longrightarrow H_{n-1}({\mathcal {A}}),}$

وخرائط الحدود هذه تجعل المتتابعة الآتية متتابعة منضبطة:

إن الخرائط ${\displaystyle \alpha _{*}^{}}$ و ${\displaystyle \beta _{*}^{}}$ هي الخرائط المعتادة المستحدثة بالتجانس، وخرائط الحدود ${\displaystyle \delta _{n}^{}}$ مشروحة أدناه.

التسمية

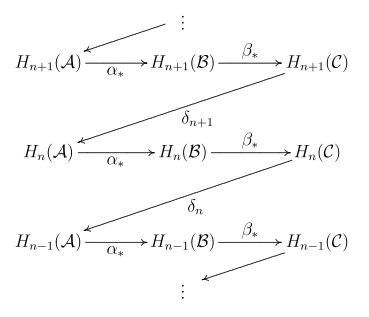
أتى اسم الفرضية من سلوك الخط المتعرج الذي تنحو نحوه خرائط الحدود في المتتابعة. في طفرة لم تعهد في علم الاصطلاح، تعرف هذه النظرية على نحو شائع أيضًا باسم فرضية الأفعى، مع أن هناك نتيجة أخرى في الجبر التجانسي بهذا الاسم. يمكن استخدام فرضية الأفعى الأخرى لإثبات فرضية الخط المتعرج بطريقة مختلفة عما سيذكر أدناه.

تكون خرائط الحدود

الخرائط ${\displaystyle \delta _{n}^{}}$ معرفة ب اجعل ${\displaystyle c\in C_{n}}$ تستعرض طائفة في ${\displaystyle H_{n}({\mathcal {C}})}$ لتكون ${\displaystyle \partial _{n}''(c)=0}$. انضباط الصف يتضمن أن تكون ${\displaystyle \beta _{n}^{}}$ شمولية، لذلك يجب أن تكون هناك بعض عناصر ${\displaystyle b\in B_{n}}$ على اعتبار أن ${\displaystyle \beta _{n}^{}(b)=c}$.

بتبادلية المخطط:

${\displaystyle \beta _{n-1}\partial _{n}'(b)=\partial _{n}''\beta _{n}(b)=\partial _{n}''(c)=0.}$

بالانضباط:

${\displaystyle \partial _{n}'(b)\in \ker \beta _{n-1}=\mathrm {im} \alpha _{n-1}.}$

ولأن ${\displaystyle \alpha _{n-1}^{}}$ تبادلية، فهناك عنصر وحيد ${\displaystyle a\in A_{n-1}}$ لتكون ${\displaystyle \alpha _{n-1}(a)=\partial _{n}'(b)}$. هذه دورة، لأن ${\displaystyle \alpha _{n-2}^{}}$ شمولية وكذلك

${\displaystyle \alpha _{n-2}\partial _{n-1}(a)=\partial _{n-1}'\alpha _{n-1}(a)=\partial _{n-1}'\partial _{n}'(b)=0,}$

ولأن ${\displaystyle \partial ^{2}=0}$، فإن ${\displaystyle \partial _{n-1}(a)\in \ker \alpha _{n-2}=\{0\}}$.

هذا يعني أن ${\displaystyle a}$ دورة، ولذلك فهي تمثل طائفة في ${\displaystyle H_{n-1}({\mathcal {A}})}$، ويمكننا الآن أن نعرف

${\displaystyle \delta _{}^{}[c]=[a].}$

يمكن بخريطة من خرائط الحدود المذكورة إظهار أنها واضحة التعريف (أي أنها مستقلة عن الخيارين c و b). يستخدم البرهان إثباتات مطاردة المخططات المشابهة لما ذكر أعلاه. وتستخدم أيضًا مثل هذه الإثباتات لإظهار أن المتتابعة المتجانسة منضبطة لدى كل مجموعة.

المراجع

• Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press.  . مؤرشف من الأصل في 19 مايو 2018.
• Munkres, James R. (1993). Elements of Algebraic Topology. New York: Westview Press.  .

موسوعات ذات صلة :

• موسوعة رياضيات