اختيار المواد

اختيار المواد هو خطوة نحو عملية تصميم أي مكون مادي. في سياق تصميم المنتج، فالهدف الرئيسي في اختيار المواد هو تحقيق أهداف المنتج بأقل التكاليف.^[1] ويذكرأن الاختيار المنهجي لأفضل المواد لمشروع معين يبدأ بتحديد خصائص وتكاليف المواد المرشح اختيارها. على سبيل المثال، يجب أن يكون للغطاء الحراري موصلية حرارية ضعيفة من أجل تقليل نقل الحرارة حسب اختلاف درجتها. و من الضروري أن يمتلك المصمم معرفة شاملة بخصائص المواد وكيفية عملها تحت ضغط البيئة العملية. و من بعض الخصائص الهامة للمواد هي : القوة والمتانة والمرونة والوزن ومقاومة الحرارة والتآكل، والقدرة على الخدش، ملحمة أم متصلبة، القدرة الميكانيكية، الموصلية الكهربائية، إلخ.^[2]

وإن الاختيار المنهجي للمشاريع التي تتطلب معايير متعددة لهو أمرأكثر تعقيدًا. على سبيل المثال، لمادة تحتاج أن تكون المادة صلبة وخفيفة، كقضيب معدني فتركيبة من معامل يونج العالي والكثافة المنخفضة مؤشر يدل على أفضل المواد، أما بالنسبة للوحٍ ما، فإن جذر مكعب الصلابة مقسومًا على الكثافة ${\displaystyle {\sqrt[{3}]{E}}/\rho }$ هو أفضل مؤشر، نظرًا لأن صلابة الثني في الصفيحة تتضاعف بمقدار سماكتها. و علاوةً على ذلك فإن أخذنا بعين الاعتبار كلاً من الصلابة والخفة من أجل سحب قضيب معدني فإن معامل المرونة النوعي أو المعامل مقسوم على الكثافة ${\displaystyle E/\rho }$ يجب أن تؤخذ في الحسبان، بينما إن كانت المادة المراد ثنيها حزمة ما، فإن المادة المصنفة ${\displaystyle {\sqrt[{2}]{E}}/\rho }$ هي أفضل مؤشر.

ولكن في الواقع غالبا ما تواجه بعض العواقب وان العامل الوظيفي يجي أن يأخذ في الاعتبار. فتكلفة المادة المثالية تعتمد على أمور عدة كالشكل والحجم والتكوين وقد تكون باهظة الثمن وشائعة الطلب ولها مواصفات معنية وحتى منطقة السوق المباعة فيه تحدد توافرها.

مخططات أشبي

مخطط يوضح معامل يونج مقابل الكثافة. تمثل الألوان أنواع المواد.

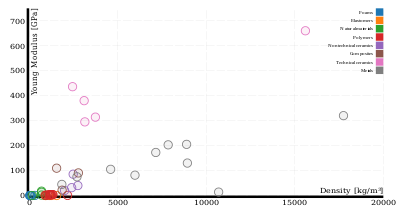
مخطط أشبي سمي بهذا الأسم تيمناْ ب مايكل أشبي من جامعة كامبريدج وهو عبارة عن مخطط مبعثر يوضح اثنين أو أكثر من الخصائص لكثير من المواد أو فئات المواد.^[3] وهذه المخططات مفيدة لمقارنة النسبة بين الخصائص المختلفة. فلنأخذ كمثال جزء التصلب / الخفة الذي تمت مناقشته أعلاه، سيكون له معامل يونغ على أحد المحاور والكثافة على المحور الآخرمع وجود نقطة بيانية واحدة على الرسم البياني لكل مادة مرشحة. ففي مخطط كهذا من السهل العثور ليس فقط على المواد ذات الصلابة الأكثر أو تلك ذات الكثافة الأقل بل معرفة المادة التي تمتلك أفضل نسبة ${\displaystyle E/\rho }$. باستخدام مقياس السجل على كلا المحورين يسهل اختيار المواد التي لديها أفضل صلابة من أجل اللوح ${\displaystyle {\sqrt[{3}]{E}}/\rho }$.

مخطط يوضح تتضاعف معامل يونغ مقابل الكثافة بالطريقة اللوغاريتمية. تمثل الألوان أنواع المواد.

يظهر المخطط الأول على اليمين الكثافة ومعامل يونغ، بمقياس خطي. ويظهر المخطط الثاني سمات المواد نفسها بمقياس لوغاريتمي. يتم تحديد عائلات المواد (البوليمرات، الرغاوي، المعادن، إلخ) من خلال الألوان.^[4]

بالإضافة إلى ارتفاع أسعار الطاقة وتطور التكنولوجيا، استبدلت السيارات كميات متزايدة من سبائك المغنيسيوم والألومنيوم خفيفة الوزن عوضاْ عن الحديد حيث حل البلاستيك المقوى بألياف الكربون وسبائك التيتانيوم محل الألومنيوم في الطائرات ومازالت الأقمار الصناعية تصنع من مواد مركبة دخيلة.

بالطبع، التكلفة لكل كيلوغرام ليست هي الأمر الأهم في اختيار المواد. بل هناك مفهوم المهم وهو "التكلفة لكل وحدة وظيفية". فمثلاْ إذا كان الهدف الرئيسي من التصميم هو الصلابة اللوحية للمادة كما هو موضح في الفقرة التمهيدية أعلاه فإن المصمم سيحتاج إلى مادة لديها المكون المثالي والمكون من الكثافة ومعامل يونج والتكلفة. فالوصول لخليط معقد من الخواص التقنية والمادية امرٌيصعب تحقيقه يدوياً ولذلك يعد برنامج الاختيار لمنطقي أداة مهمة.

صورة عامة حول استخدام مخطط أشبي

يعد استخدام "مخطط أشبي" أمر شائع في اختيار المادة المناسبة. أولاً يتم تحديد ثلاث مجموعات مختلفة من المتغيرات:

• متغيرات المواد هي الخصائص الكامنة لمادة مثل الكثافة، المعامل، نقطة الخضوع، وغيرها من ذلك.
• المتغيرات الحرة هي كميات يمكن أن تتغير خلال دورة التحميل، مثلاً القوة المنسوبة.
• متغيرات التصميم هي حدودٌ مفروضةٌ على التصميم، مثل مدى سماكة الحزمة أو مقدار انحرافها

بعد ذلك، يتم اشتقاق معادلة لمؤشر الأداء. وهذه المعادلة تحدد رقميا قدرة المادة المراد اختيارها في وضع معين. حسب الاصطلاح، كلما كان مؤشر الأداء عالي أشارذلك إلى مادة أفضل. أخيرًا، يتم رسم مؤشر الأداء على مخطط أشبي. وبالمعاينة النظرية تحدد المادة المرغوبة.

مثال على استخدام مخطط أشبي

في هذا المثال، ستخضع المواد لكل من الضغط والثني. لذلك، فإن المادة المثالية ستعمل بشكل جيد في كلتا الحالتين.

مؤشر الأداء أثناء الضغط

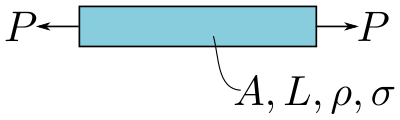
في الحالة الأولى، واجه القضيب المعدني قوتين: وزن الجاذبية ${\displaystyle w}$ والتوتر ${\displaystyle P}$. ومتغير المادة هو الكثافة ${\displaystyle \rho }$ والقوة ${\displaystyle \sigma }$. افترض أن الطول ${\displaystyle L}$ والتوتر ${\displaystyle P}$ تم تعديلهما، مما يجعلها من متغيرات التصميم. وأخيرا عبر منطقة المقطع ${\displaystyle A}$ هو متغير حر. فالهدف في هذه الحالة هو تقليل الوزن ${\displaystyle w}$ عن طريق اختيار مادة مع أفضل مزيج من متغيرات المواد ${\displaystyle \rho ,\sigma }$. يوضح الشكل 1 هذا التحميل.

شكل 1. قضيب وضع تحت تأثير ضغط الشد والإجهاد لتقليل الوزن.

يتم قياس الضغط في القضيب ب ${\displaystyle P/A}$ في حين وصف الوزن ${\displaystyle w=\rho AL}$. يتطلب اشتقاق مؤشر الأداء إزالة جميع المتغيرات الحرة، مع ترك متغيرات التصميم ومتغيرات المواد فقط. في هذه الحالة يجب إزالة ${\displaystyle A}$. يمكن إعادة ترتيب معادلة الضغط المحوري لإعطاء ${\displaystyle A=P/\sigma }$. استبدال هذا في معادلة الوزن يعطي ${\displaystyle w=\rho (P/\sigma )L=\rho LP/\sigma }$. بعد ذلك، يتم تجميع متغيرات المواد ومتغيرات التصميم بشكل منفصل، لينتج ${\displaystyle w=(\rho /\sigma )LP}$.

منذ وبما أن كلاً من ${\displaystyle L}$ و ${\displaystyle P}$ تم تعديلهما، وأن الهدف من ذلك هو لتقليل ${\displaystyle w}$ حينها يجب تقليل معدل النسبة ${\displaystyle \rho /\sigma }$. ومع ذلك، وفقًا للمعايير، يكون مؤشر الأداء دائمًا ما يكون كمياً لأقصى حد ممكن. لذلك، المعادلة الناتجة هي ${\displaystyle {\text{Performance index}}=P_{cr}=\sigma /\rho }$

مؤشر الأداء خلال عملية الثني

تالياً، لنفترض أن المادة تخضع أيضًا لقوى الانحناء. فإن الحد الأقصى لمعادلة تركيز الشد للانحناء هو ${\displaystyle \sigma =(-My)/I}$، حيث أن ${\displaystyle M}$ هي لحظة الانحناء، و ${\displaystyle y}$ هي المسافة من المحور المحايد، و ${\displaystyle I}$ هي لحظة الجمود. وهذا موضح في الشكل 2. باستخدام معادلة الوزن أعلاه وحل للمتغيرات الحرة، فإن الحل الذي تم التوصل إليه هو ${\displaystyle w={\sqrt {6MbL^{2}}}(\rho /{\sqrt {\sigma }})}$، أي أن ${\displaystyle L}$ هو الطول و ${\displaystyle b}$ هو ارتفاع القضيب. افترض أن ${\displaystyle b}$، ${\displaystyle L}$ و ${\displaystyle M}$ هي متغيرات تصميم معدلة، فسيصبح مؤشر الأداء للانحناء ${\displaystyle P_{CR}={\sqrt {\sigma }}/\rho }$.

الشكل 2. القضيب المعدني تحت تأثير ضغط الانحناء. لمحاولة تقليل الوزن

اختيار المادة الأفضل ككل

عند هذه النقطة، تم اشتقاق مؤشران للأداء: للتوتر ${\displaystyle \sigma /\rho }$ وللانحناء ${\displaystyle {\sqrt {\sigma }}/\rho }$. تتمثل الخطوة الأولى في إنشاء مخطط لوغاريتمي وإضافة جميع المواد المعروفة في المواقع المناسبة. ولكن، يجب تعديل معادلات مؤشر الأداء قبل أن يتم رسمها على الرسم اللوغاريتمي.

لمعادلة أداء التوتر ${\displaystyle P_{CR}=\sigma /\rho }$، الخطوة الأولى هي أخذ لوغاريتم لكلا الجانبين. يمكن إعادة ترتيب المعادلة الناتجة لإعطاء ${\displaystyle \log(\sigma )=\log(\rho )+\log(P_{CR})}$. لاحظ أن هذا يتبع تنسيق ${\displaystyle y=x+b}$، مما يجعلها خطية على الرسم اللوغاريتمي. وبالمثل، فإن تقاطع y هو لوغاريتم ${\displaystyle P_{CR}}$. وبالتالي، فإن قيمة ${\displaystyle P_{CR}}$ المعدلة للتوتر في الشكل 3 هو 0.1.

معادلة أداء الثني ${\displaystyle P_{CR}={\sqrt {\sigma }}/\rho }$ يمكن التعامل معها بالمثل. وباستخدام خاصية القوة اللوغاريتمية يمكن استخلاص ذلك ${\displaystyle \log(\sigma )=2\times (\log(\rho )+\log(P_{CR}))}$. قيمة ل ${\displaystyle P_{CR}}$ للانحناء ≈ 0.0316 في الشكل 3. وأخيرًا، يتم رسم كلا الخطين على مخطط أشبي.

الشكل 3. مخطط أشبي مع مؤشرات الأداء المرسومة لتحقيق أقصى نتيجة

أولاً، يمكن العثور على أفضل مواد للانحناء عن طريق التحقق من المناطق التي تتجاوزخط الانحناء على الرسم البياني من ${\displaystyle {\sqrt {\sigma }}/\rho }$. في هذه الحالة، تكون بعض الرغاوي (باللون الأزرق) والسيراميك التقني (باللون الوردي) أعلى من الخط. وبذلك تكون هذه أفضل المواد للانحناء. وعلى الصعيد المقابل، فإن المواد الموجودة أسفل الخط (مثل المعادن الموجودة في أسفل يمين المنطقة الرمادية) ستكون أسوأ المواد.

وأخيراً، فإن خط التوتر${\displaystyle \sigma /\rho }$ يمكن استخدامه "لكسر الحواجز" بين الرغاوي والسيراميك التقني. نظرًا لأن السيراميك التقني هو المادة الوحيدة التي تتواجد في مستوى أعلى من خط التوتر، لذا فإن أفضل مادة تعمل تحت تأثير الضغط هو السيراميك التقني. وبذلك، فإن أفضل المواد بشكل عام هي السيراميك الفني في الجزء العلوي الأيسر من المنطقة الوردية مثل كربيد البورون.

فهم الرسم بشل رقمي

يمكن رسم مؤشر الأداء على مخطط أشبي عن طريق تحويل المعادلة إلى المقياس اللوغاريتمي. يتم ذلك عن طريق أخذ لوغاريتم كلا الجانبين، ووضها بمحاذاة خط مشابهًا لخط مع ${\displaystyle P_{cr}}$ كونها تقاطع المحور ص. وهذا يعني أنه كلما زاد التقاطع، زاد أداء المادة. عن طريق تحريك الخط لأعلى في مخطط أشبي، يرتفع مؤشر الأداء. لكل مادةٍ تمر الخط، لديهتسجل مؤشرات أدائها على المحور ص. لذلك، فإن الانتقال إلى أعلى المخطط مع استمرار لمس منطقة من المواد هو المكان الذي سيكون فيه أعلى أداء للمادة.

وكما يتضح من الشكل 3، يتقاطع الخطان بالقرب من أعلى الرسم البياني وهما السيراميك التقني والمركبات. هذا سيعطي مؤشر أداء 120 لتحمل الشد و 15 للثني. عند الأخذ في الاعتبار تكلفة السيراميك الهندسي، خاصة وأن التقاطع حصل بالقرب من كربيد البورون، فلن يكون هذا الاختيار الأمثل. هناك حالة أفضل مع انخفاض مؤشر الأداء ولكن هنالك حلول لها تكلفة أقل حول هندسة المركبات بالقرب من CFRP (صفائح أنسجة الكربون المدعمة).

المراجع

موسوعات ذات صلة :

• موسوعة علم المواد
• موسوعة صناعة
• موسوعة تقانة
• موسوعة إلكترونيات