متجه لابلاس-رنج-لنز

متجه لابلاس رنج لنز (Laplace–Runge–Lenz vector)‏ واختصاره متجه LRL في ميكانيكا كلاسيكية، هو متجه يُستخدم لتوضيح شكل و هيئة مدار جسم فلكي حول جسم آخر، كدوران كوكب حول نجم.

لجسمان متجاوبان مع جاذبية نيوتن، متجه LRL هو ثابت الحركة، بمعنى أنه ثابت مهما تم حسابه على أي مكان في المدار.^[1] بِوَجْهِ العُمُوم، متجه لابلاس-رنج-لنز محفوظ في كل المسائل التي تخص تجاوب جسمين مع القوة المركزية التي تختلف باختلاف التربيع العكسي للمسافة بينهما، تُسمى هذه المسائل بمسائل كبلر.^[2]

ذرة الهيدروجين هي مسألة من مسائل كبلر، بسبب إنها تشمل جُسيمات تتجاوب مع قانون كولوم لكهروستاتيكا، قوة عكسية مُربعة أخرى. هذا المتجه مهم في لأول استنتاج في مجال ميكانيكا الكم لطيف ذرة الهيدروجين،^[3] قبل استحداث معادلة شرودنغر. لكن هذه الطريقة لم تُعد تُستخدم اليوم بكثرة.

في الميكانيكا الكلاسيكية وميكانيكا الكم، الكميات المحفوظة عموماً ترتبط بتماثل النظام، متجه LRL يرتبط بتماثل غير معتاد؛ مسألة كبل رياضياً تكافأ لجسيم يتحرك بحرية علي سطح رباعي أبعاد الكرة. وبالتالي النظام بالكامل متماثل تحت دورانات مُعينة لفراغ رباعي الأبعاد.^[4] هذا التماثل نتيجة خاصيتان من خواص مسائل كبلر: متجه السرعة دائماً يتحرك في دائرة مثالية، وجميع سرعات هذه الدوائر تتقابل في نفس النقطتان.^[5]

سُمي متجه لابلاس- رنج- لنز بعد بيير لابلاس، كارل رنج، وويلهيلم لنز. يُعرف أيضاً باسم متجه لابلاس، متجه رنج، ومتجه لنز. من سخرية القدر لم يتم اكتشاف هذا المتجه عن طريق هؤلاء العلماء. هذا المتجه أُعيد اكتشافه أكثر من مرة،^[6] و هو أيضاً متكافأ مع متجهة الشذوذ لميكانيكا سماوية.^[7] تم تعريف تعميمات مختلفة لمتجه LRL، التي تدمج تأثيرات النسبية الخاصة، مجال كهرومغناطيسي، وأنواع مختلفة من قوى مركزية.

شرح

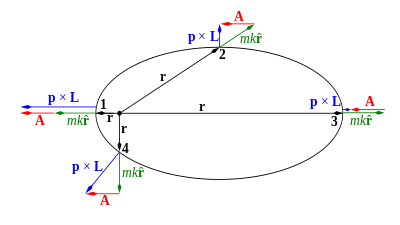
جسيم مُفرد يتحرك تحت تأثير قوة مركزية محفوظة الطاقة لديها على الأقل أربع ثوابت حركة، الطاقة الكلية E، والثلاث مركبات الكارتيزية لمتجه الزخم الزاوي L بالنسبة إلى نقطة الأصل. مدار الجسيم محجوز بمستوى مُعرف بزخم الحركة الأولي للجسيم p ( أو متكافأ مع سرعته v) و متجه r بين الجسيم ومركز القوة. متجه A (متجه LRL) دائماً يقع في مستوي حركة أي قوة مركزية. لكن A ثابت فقط لتربيع العكسي للقوة المركزية.^[8] لمعظم القوي المركزية، متجه A غير ثابت، لكن يتغير في الطول والإتجاه؛ إذا كانت القوة المركزية تقريباً قانون التربيع العكسي، كان متجه A ثابت الطول ولكن يدور ببطء في إتجاهه. يمكن أن يُعرف متجه A لكل القوي المركزية، لكنه دالة معقدة في المكان، وعادةً لا يمكن توضيحه في نموذج مغلق.^[9][10]

مستوى الحركة عمودي علي متجه زخم زاوي L؛ هذا يكون موضحاً رياضياً متجه الجداء القياسي r·L = 0، بالمثل A·L = 0 لأن متجه A يقع في نفس المستوى.

تاريخ إعادة اكتشافه

لم يكن متجه A معروف من قِبل الفيزيائين لهذا تم إعادة اكتشافه أكثر من مرة في خلال الثلاث القون الأخيرة.^[6] جاكوب هيرمان كان أول من وضح ان متجه A حُفظ نتيجة أنه حالة خاصة من التربيع العكسي للقوة المركزية.^[11] عمل هيرمان تم إعادة صياغه في نموذج حديث علي يد يوهان بيرنولي عام 1710.^[12] في نهاية هذا القرن إستنتج بيير لابلاس متجه A بشكل تحليلي بدلاً من شكله الهندسي.^[13] في منتصف القرن التاسع عشر، وليم روان هاملتون إستنتج متجه الشذوذ المكافأ له.^[7]

تعريف رياضي

لجسيم مُنفرد مُتأثر بقوة مركزية معادلته تكون:

${\displaystyle \mathbf {F} (r)={\frac {-k}{r^{2}}}\mathbf {\hat {r}} ~,}$

متجه LRL تعريفه رياضياً:^[8]

${\displaystyle \mathbf {A} =\mathbf {p} \times \mathbf {L} -mk\mathbf {\hat {r}} }$

حيث:

• m كتلة الجسيم المُتحرك تحت قوة مركزية.
• p هو زخم الحركة.
• L = r × p هو متجه زخم زاوي.
• k هو معيار يوضح شدة القوة المركزية.
• r هو متجه المكان للجسيم.
• ${\displaystyle \mathbf {\hat {r}} \!\,}$ هو متجه وحدة؛ ${\displaystyle \mathbf {\hat {r}} ={\frac {\mathbf {r} }{r}}}$ حيث r هي مقدار r.

لأن القوة المفروضة هي قوة محفوظة، الطاقة الكلية E تكون ثابتة الحركة،

${\displaystyle E={\frac {p^{2}}{2m}}-{\frac {k}{r}}={\frac {1}{2}}mv^{2}-{\frac {k}{r}}~.}$

أيضاً القوة المفروضة هي قوة مركزية، وبالتالي متجه L يصبح محفوظ أيضاً ويحدد المستوي الذي يمر به الجسيم. متجه LRL عمودي علي متجه L بسبب أن p × L و r عمودي علي L.

استنتاج مدارات كبلر

شكل واتجاه مدارات مسائل كبلر يمكن تحديدها عن طريقمتجه LRL كالتالي:^[8]

${\displaystyle \mathbf {A} \cdot \mathbf {r} =Ar\cos \theta =\mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)-mkr}$

حيث θ هي الزاوية بين A , r.

${\displaystyle \mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)=\left(\mathbf {r} \times \mathbf {p} \right)\cdot \mathbf {L} =\mathbf {L} \cdot \mathbf {L} =L^{2}}$

بعد الترتيب تعريف المعادلة لقطع مخروطي تكون:

${\displaystyle {\frac {1}{r}}={\frac {mk}{L^{2}}}\left(1+{\frac {A}{mk}}\cos \theta \right)}$

انحراف مداري e

${\displaystyle e={\frac {A}{mk}}={\frac {\left|\mathbf {A} \right|}{mk}}}$

و الوتر البؤري

${\displaystyle \left|2\ell \right|={\frac {2L^{2}}{mk}}~.}$

المحور الكبير a للقطع المخروطي يكون:

${\displaystyle a\left(1\pm e^{2}\right)=\ell ={\frac {L^{2}}{mk}}~,}$

حيث قطع ناقص تكون إشارته سالِب و إشارة قطع زائد تكون موجبه.

مراجع

موسوعات ذات صلة :

• موسوعة ميكانيكا الكم
• موسوعة هندسة تطبيقية
• موسوعة الفيزياء