النمذجة الجزيئية تشمل جميع الأساليب ، النظرية والحاسوبية ، وتستخدم لنمذجة أو محاكاة سلوك الجزيئات. وتستخدم هذه الأساليب في مجالات الكيمياء الحاسوبية وتصميم الأدوية وعلم الأحياء الحسابي وعلوم المواد لدراسة النظم الجزيئية التي تتراوح من النظم الكيميائية الصغيرة إلى الجزيئات البيولوجية الكبيرة وتجميعات المواد. يمكن إجراء أبسط العمليات الحسابية يدويًا ، ولكن لا بد حتمًا من أجهزة الكمبيوتر إجراء النمذجة الجزيئية لأي نظام ذي حجم معقول. الميزة المشتركة لطرق النمذجة الجزيئية هي وصف المستوى الذري للأنظمة الجزيئية. قد يشمل ذلك معالجة الذرات باعتبارها أصغر وحدة فردية (نهج ميكانيكي جزيئي) ، أو نمذجة إلكترونات صريحة لكل ذرة (مقاربة كيميائية كمومية).يمكن إجراء العمليات الحسابية يدويًا ، ولكن لا بد من وجود أجهزة كمبيوتر لإجراء النمذجة الجزيئية لأي نظام ذي حجم معقول. الميزة المشتركة لطرق النمذجة الجزيئية هي وصف المستوى الذري للأنظمة الجزيئية. وقد يشمل ذلك معالجة الذرات باعتبارها أصغر وحدة فردية (نهج ميكانيكا جزيئي) ، أو نمذجة إلكترونات صريحة لكل ذرة (نهج كيميائي كمومي).
ميكانيكا جزيئية
ميكانيكا جزيئية الميكانيكا الجزيئية هي أحد جوانب النمذجة الجزيئية ، لأنها تنطوي على استخدام الميكانيكا الكلاسيكية (الميكانيكا النيوتنية) لوصف الأساس المادي وراء النماذج. تصف النماذج الجزيئية عادةً الذرات (النواة والإلكترونات بشكل جماعي) كرسوم نقطية مع كتلة مقترنة. تم وصف التفاعلات بين الذرات المجاورة بتفاعلات تشبه الربيع (تمثل الروابط الكيميائية) وقوى فان در فالس. يتم استخدام إمكانات لينارد جونز لوصف الأخير. يتم حساب التفاعلات الإلكتروستاتيكية وفقًا لقانون كولوم. يتم تعيين ذرات الإحداثيات في الفضاء الديكارتية أو في الإحداثيات الداخلية ، ويمكن أيضا أن يتم تعيين السرعات في المحاكاة الديناميكية. ترتبط السرعات الذرية بدرجة حرارة النظام ، وهي كمية آبيرة. ويطلق على التعبير الرياضي الجماعي وظيفة محتملة ويرتبط بالطاقة الداخلية للنظام (U) ، وهي كمية ديناميكية حرارية تعادل مجموع الطاقات الكامنة والحركية. وتسمى الطرق التي تقلل من الطاقة الكامنة طرق تقليل الطاقة (على سبيل المثال ، أكثر انحدارًا وتدرجًا مترافقًا) ، بينما تسمى الطرق التي تصف سلوك النظام مع انتشار الوقت الديناميكيات الجزيئية.هذه الدالة ، المشار إليها كدالة محتملة ، تحسب الطاقة الكامنة الجزيئية كمجموع لمصطلحات الطاقة التي تصف انحراف أطوال الرابطة وزوايا الرابطة وزوايا الالتواء بعيدًا عن قيم التوازن ، بالإضافة إلى المصطلحات الخاصة بالأزواج غير المرتبطة من الذرات التي تصف الشاحنة der Waals والتفاعلات الكهروستاتيكية. إن مجموعة المعلمات المكونة من أطوال الرابطة المتوازنة وزوايا الرابطة وقيم الشحنة الجزئية وثوابت القوة ومعلمات فان در والاس يطلق عليها مجتمعة حقل قوة. تستخدم التطبيقات المختلفة للميكانيكا الجزيئية تعبيرات رياضية مختلفة ومعلمات مختلفة للوظيفة المحتملة. تم تطوير حقول القوة الشائعة المستخدمة اليوم باستخدام حسابات كمية عالية المستوى و / أو ملائمة للبيانات التجريبية. تُستخدم الطريقة ، التي يُطلق عليها اسم "تصغير الطاقة" ، لإيجاد مواضع ذات تدرج صفري لجميع الذرات ، وبعبارة أخرى ، حد أدنى محلي للطاقة. حالات الطاقة المنخفضة أكثر استقرارًا ويتم التحقيق فيها عمومًا بسبب دورها في العمليات الكيميائية والبيولوجية. من ناحية أخرى ، تحاكي محاكاة الديناميات الجزيئية سلوك النظام كدالة للوقت. وهو ينطوي على حل قوانين نيوتن للحركة ، وبشكل أساسي القانون الثاني ، {\ mathbf {F}} = m {\ mathbf {a}}. يؤدي دمج قوانين نيوتن للحركة ، باستخدام خوارزميات تكامل مختلفة ، إلى مسارات ذرية في المكان والزمان. تعرف القوة على الذرة بأنها التدرج السلبي لوظيفة الطاقة المحتملة. إن طريقة تقليل الطاقة مفيدة للحصول على صورة ثابتة للمقارنة بين حالات أنظمة مشابهة ، بينما توفر الديناميكيات الجزيئية معلومات حول العمليات الديناميكية مع التضمين الجوهري لتأثيرات درجات الحرارة.
المتغيرات
يمكن تشكيل الجزيئات إما في فراغ ، أو في وجود مذيب مثل الماء. ويشار إلى محاكاة النظم في الفراغ على أنها محاكاة طور الغاز ، بينما يشار إلى تلك التي تشمل وجود جزيئات المذيبات كمحاكاة صريحة للمذيبات. في نوع آخر من المحاكاة ، يتم تقدير تأثير المذيب باستخدام تعبير رياضي تجريبي. هذه تسمى عمليات المحاكاة الضمنية.
تنسيق التمثيل
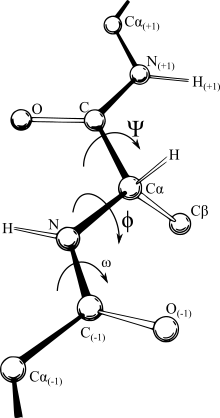
معظم حقول القوة تعتمد على المسافة ، مما يجعل التعبير الأكثر ملاءمة لهذه الإحداثيات الديكارتية. ومع ذلك ، فإن الطبيعة الصلبة نسبياً للسندات التي تحدث بين ذرات معينة ، وفي جوهرها ، تحدد ما يقصد به جزيء التسمية ، تجعل نظام إحداثيات داخلي هو التمثيل الأكثر منطقية. في بعض المجالات ، يُطلق على التمثيل IC (طول الرابطة ، الزاوية بين الروابط ، وزاوية الالتواء للسند كما هو موضح في الشكل) تمثيل الزاوية Z-matrix أو الالتواء. لسوء الحظ ، تتطلب الحركات المستمرة في الفضاء الديكارتية غالبًا أغصانًا زاويًا متقطعة في الإحداثيات الداخلية ، مما يجعل العمل مع حقول القوة في تمثيل الإحداثي الداخلي أمرًا صعبًا ، وبالعكس ، قد لا يكون التشريد البسيط لذرة في الفضاء الديكارتي مسارًا مستقيًا إلى حظر السندات المترابطة. وبالتالي ، فمن الشائع جداً أن تقوم البرامج الحسابية المحسّنة بالرجوع ذهاباً وإياباً بين التمثيلات أثناء تكرارها. هذا يمكن أن تهيمن على وقت الحساب من نفسه ، وفي الجزيئات سلسلة طويلة إدخال التعددية العددية التراكمية. في حين أن جميع خوارزميات التحويل تنتج نتائج متطابقة رياضيا ، إلا أنها تختلف من حيث السرعة والدقة العددية. حالياً ، التواء الأسرع والأكثر دقة للتحويل الديكارتي هو أسلوب الإطار المرجعي .
التطبيقات
يتم الآن استخدام طرق النمذجة الجزيئية بشكل روتيني للتحقق من البنية ، الديناميات ، خصائص السطح ، والديناميكا الحرارية للأنظمة غير العضوية والبيولوجية والبوليمرية. تشتمل أنواع النشاط البيولوجي التي تم بحثها باستخدام النمذجة الجزيئية على طي البروتين ، وتحفيز الإنزيم ، واستقرار البروتين ، والتغيرات التوافقية المرتبطة بالوظيفة الحيوية الجزيئية ، والاعتراف الجزيئي للبروتينات ، والحمض النووي ، والمجمعات الغشائية.