
| Naissance | Petoskey |
|---|---|
| Décès |
(à 84 ans) Medford |
| Sépulture |
Cimetière de Mount Auburn |
| Nom dans la langue maternelle |
Claude Elwood Shannon |
| Nationalité | |
| Domicile |
Gaylord |
| Formation |
Gaylord High School (en) (jusqu'en ) Université du Michigan (- Massachusetts Institute of Technology (- |
| Activités |
Mathématicien, professeur d'université, ingénieur, inventeur, cryptographe, informaticien, généticien |
| Conjoints |
Norma Barzman (de à ) Betty Shannon (en) (à partir de ) |
| A travaillé pour |
Massachusetts Institute of Technology (- Laboratoires Bell (- Institute for Advanced Study (- |
|---|---|
| Membre de |
Académie américaine des sciences () Académie américaine des arts et des sciences () Académie Léopoldine () Académie royale néerlandaise des arts et des sciences () Société américaine de philosophie () Royal Society () |
| Sport | |
| Directeurs de thèse |
Frank Lauren Hitchcock (en), Vannevar Bush |
| Influencé par |
Vannevar Bush, Ralph Hartley |
| Distinctions | Liste détaillée Médaille commémorative IEEE Morris N. Liebmann () Médaille Stuart-Ballantine (en) () Conférence Gibbs () National Medal of Science () IEEE Medal of Honor () Prix Claude-Shannon () Prix Harvey () Edwin Howard Armstrong Achievement Award () Prix Harold-Pender () Médaille John Fritz (en) () Kyoto Prize in Basic Sciences () Membre étranger de la Royal Society () Prix Marconi () National Inventors Hall of Fame () |
| Archives conservées par |
Une théorie mathématique de la communication, A Symbolic Analysis of Relay and Switching Circuits (d), théorème d'échantillonnage, théorème du codage de source, deuxième théorème de Shannon |
Claude Elwood Shannon ( à Petoskey[2], Michigan - à Medford, Massachusetts) est un ingénieur en génie électrique et mathématicien américain. Il est l'un des pères, si ce n'est le père fondateur, de la théorie de l'information.
Biographie
Enfance et études
Les parents de Claude Shannon étaient Claude Elwood Shannon et Mabel Catherine Wolf[3].
Il étudie le génie électrique et les mathématiques à l'université du Michigan dont il est diplômé en 1936[3]. Il utilise notamment l'algèbre de Boole pour sa maîtrise soutenue en 1938 au Massachusetts Institute of Technology (MIT). Il y explique comment construire des machines à relais en utilisant l'algèbre de Boole pour décrire l'état des relais (1 : fermé, 0 : ouvert). Il obtient un doctorat (PhD) en mathématiques au MIT en 1940[3].
Période laboratoires Bell
Shannon travaille vingt ans au MIT, de 1958 à 1978. Parallèlement à ses activités universitaires, il travaille aussi aux laboratoires Bell de 1941 à 1972[3].
En 1949, il se marie avec Mary Elizabeth Moore, avec qui il aura trois enfants[3].
Maladie et mort
Souffrant de la maladie d'Alzheimer dans les dernières années de sa vie, Claude Shannon est mort à 84 ans le à Medford dans le Massachusetts[3].
Personnalité
Claude Shannon est connu non seulement pour ses travaux dans les télécommunications, mais aussi pour l'étendue et l'originalité de ses hobbies, comme la jonglerie, la pratique du monocycle et l'invention de machines farfelues : une souris mécanique sachant trouver son chemin dans un labyrinthe, un robot jongleur, un joueur d'échecs (roi tour contre roi), etc.
L'un de ces « gadgets » présente toutefois un grand intérêt conceptuel, comme le montrent Philippe Boulanger et Alain Cohen dans Le Trésor des paradoxes (Éditions Belin, 2007) : « Claude Shannon voulut élaborer une « machine inutile », sans finalité : on la met en marche en appuyant, comme sur tout dispositif électromécanique, sur une touche « on » ; mais les choses prennent alors une tournure surprenante, car cette mise sous tension déclenche un mécanisme provoquant aussitôt l’arrêt du gadget en mettant l’interrupteur sur « off ».
Travaux
Pendant la Seconde Guerre mondiale, Shannon travaille pour les services secrets de l'armée américaine, en cryptographie, chargé de localiser de manière automatique dans le code ennemi les parties signifiantes cachées au milieu du brouillage. Son travail est exposé dans un rapport secret (déclassifié dans les années 1980 seulement), qui donne naissance après-guerre à un article, A Mathematical Theory of Communication (1948), qui fut repris en 1949 sous forme de livre publié par l'université de l'Illinois avec les commentaires de Warren Weaver, coordonnateur (Mattelart et Mattelart, 2004) dans les services secrets. Cet ouvrage est centré autour de la problématique de la transmission du signal.
Schéma de Shannon
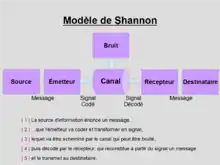
Pour décrire la communication entre machines, l'article de 1948 et le livre de 1949 commencent tous deux par un « schéma », appelé schéma de Shannon ou modèle de Shannon et Weaver. Le schéma modélise la communication entre machines :
Ce schéma est la traduction « civile » d'un schéma préalable, utilisé dans le contexte militaire :
- source → encodeur → signal → décodeur → destinataire, dans un contexte de brouillage.
Conçu pour décrire la communication entre machines, ce schéma ne prétend pas traiter exhaustivement de la communication humaine, mais son succès est suffisant pour lui mériter l'attention et des compléments de Léon Brillouin[4], et il a participé largement à la création d'un champ disciplinaire : les SIC. Shannon s'étonna de ce phénomène et s'en dissocia. Cette méthode est compatible avec une approche béhavioriste des médias. Par ailleurs, ce schéma dit canonique donne un cadre mathématique à des concepts avant lui plus flous. Ce cadre sera utilisé pour expliquer le codage de Huffman, puis des compresseurs comme ceux de Lempel-Ziv. Il sera enfin utilisé par Benoît Mandelbrot pour expliquer et rectifier la Loi de Zipf.
Shannon : l'unité de mesure
Dans l'article comme dans son livre, Claude Shannon popularise l'utilisation du mot bit comme mesure élémentaire de l'information numérique. John Tukey fut néanmoins le premier à utiliser le terme[5]. Plus précisément, le bit désigne un chiffre binaire permettant de coder une quantité d'information. Ainsi, il faut au moins un bit (ou 1 Shannon) pour coder deux états (par exemple « pile » et « face », ou plus généralement 0 et 1) et deux bits permettent de coder quatre états (00, 01, 10, 11). Les 26 lettres de l'alphabet nécessitent au minimum 5 bits car :
Plus généralement, si est le nombre d'états possibles, le nombre de bits minimum n nécessaire pour les coder tous vérifie :
(autrement dit, n est le plafond du logarithme binaire de P : )
Dans un cas idéal où toute l'information disponible est utilisée, .
Si les signes ne sont pas équiprobables (ce qui est le cas des lettres dans un message en langue naturelle), on peut obtenir un codage statistiquement plus court, en représentant les lettres fréquentes par des signaux courts (comme dans le code Morse.
Relation de Shannon
Dans le domaine des télécommunications, la relation de Shannon permet de calculer la valence (ou nombre maximal d'états) en milieu perturbé :
Soit S la puissance du signal, N la puissance du bruit :
On a alors le débit maximal d'un canal de communication de bande passante H :
Ce résultat est indépendant de la vitesse d'échantillonnage et du nombre de niveaux d'un échantillon (la valence).
Entropie au sens de Shannon
Un apport essentiel des travaux de Shannon concerne la notion d'entropie. Si l'on considère N événements de probabilité p1, p2… pN, indépendants les uns des autres, alors leur entropie de Shannon est définie comme :
Entropie =
Il a par ailleurs :
- établi un rapport entre augmentation d'entropie et gain d'information ;
- montré l'équivalence de cette notion avec l’entropie de Ludwig Boltzmann en thermodynamique.
La découverte du concept ouvrait ainsi la voie aux méthodes dites d'entropie maximale (voir probabilité), donc au scanner médical, à la reconnaissance automatique des caractères et à l'apprentissage automatique.
Théorèmes
Son nom est associé à plusieurs théorèmes, le théorème d'échantillonnage de Nyquist-Shannon sur l'échantillonnage (aussi appelé critère de Shannon), le premier théorème de Shannon sur la limite théorique de la compression, le deuxième théorème de Shannon sur la capacité d'un canal de transmission.
En dehors de la théorie de l'information
En 1981, Claude Shannon a commencé à écrire un article intitulé Scientific Aspects of Juggling, sur l'art de la jonglerie. Cet article était prévu pour être publié dans Scientific American, mais ce ne fut finalement pas le cas. Néanmoins, cette ébauche a servi de base à la formalisation des mouvements de jonglerie par le siteswap[6].
Au jeu d'échecs, il a estimé le nombre de parties différentes possibles ayant un sens échiquéen (nombre à distinguer du nombre, beaucoup plus élevé, de parties possibles que permettent les règles du jeu). Ce nombre est estimé à 10120 et porte le nom de nombre de Shannon.
Hommages
Le prix Claude-Shannon est décerné par l'association pour la théorie de l'information de l'IEEE depuis 1972, pour honorer les contributions importantes à ce domaine[7].
L'année 2016 marque le centenaire de sa naissance. La Société mathématique de France annonce une conférence de Josselin Garnier à la Bibliothèque nationale de France : Claude Shannon et l'avènement de l'ère numérique ()[8] et l'Institut Henri-Poincaré organise avec le Conservatoire national des arts et métiers l'exposition temporaire : Claude Shannon : le magicien des codes[9].
Dans son roman, La Théorie de l'information (2012), Aurélien Bellanger rend hommage au travail de Shannon. Claude Shannon est un personnage central du livre de James Gleick L'information : L'histoire - La théorie - Le déluge (Cassini, 2015, pour la traduction française).
Notes et références
- ↑ « https://archivesspace.mit.edu/repositories/2/resources/880 »
- ↑ (en) Biography of Claude Elwood Shannon, AT&T People and Organization
- 1 2 3 4 5 6 (en) John J. O'Connor et Edmund F. Robertson, « Claude Shannon », sur MacTutor, université de St Andrews, (consulté le ).
- ↑ https://hal.science/hal-03178276v2/file/Th%C3%A9orie%20information.pdf
- ↑ (en) Bit Definition, The Linux Information Project.
- ↑ (en) The Invention of Juggling Notations, The Internet Juggling Database, Arthur Lewbel, 14 octobre 2004
- ↑ « Claude E. Shannon Award », sur IEEE Information Theory Society
- ↑ « Conférence BnF 2016 - J. Garnier | Société Mathématique de France », sur smf.emath.fr (consulté le )
- ↑ Exposition : Claude Shannon : le magicien des codes.
Voir aussi
Articles connexes
- Théorème d'échantillonnage de Nyquist-Shannon
- Théorie de l'information
- A Mathematical Theory of Communication
- Communication
- Message (communication)
- Inférence bayésienne
- Cybernétique
- Norbert Wiener
- Nombre de Shannon
- Lothar Budach
Bibliographie
- Mattelart A. et Mattelart M., Histoire des théories de la communication, 3e édition, Éditions La Découverte, Paris, 2004
- Claude E. Shannon, A Symbolic Analysis of Relay and Switching Circuits, Thesis (M.S.), Massachusetts Institute of Technology, Dept. of Electrical Engineering, 1940 (lire)
- Claude E. Shannon, A Mathematical Theory of Communication, Bell System Technical Journal, vol. 27, p. 379-423 and 623-656, July and October, 1948 (ISBN 0252725484) (lire [PDF])
- Claude E. Shannon, Communication Theory of Secrecy Systems, Bell System Technical Journal, Vol 28, p. 656-715, Oct 1949. (lire)
- Claude E. Shannon et Warren Weaver, The Mathematical Theory of Communication, The University of Illinois Press, Urbana, Illinois, 1949. (ISBN 0-252-72548-4). Trad. fr. Claude Shannon and Warren Weaver: La théorie mathématique de la communication, Cassini, Paris, 2018. (ISBN 978-2-84225-222-9)
Liens externes
- Creative Thinking, Claude Shannon aux Bell Lab.
- Ressources relatives à la recherche :
- (en) Digital Bibliography & Library Project
- (en) Google Scholar
- (en) Mathematics Genealogy Project
- (mul) Scopus
- Notices dans des dictionnaires ou encyclopédies généralistes :







