Description

• Choisir k points qui représentent la position moyenne des partitions m₁⁽¹⁾, …, m_k⁽¹⁾ initiales (au hasard par exemple) ;
• Répéter jusqu'à ce qu'il y ait convergence :

– affecter chaque observation à la partition la plus proche (c.-à-d. effectuer une partition de Voronoï selon les moyennes) :

${\displaystyle S_{i}^{(t)}=\left\{\mathbf {x} _{j}:{\big \|}\mathbf {x} _{j}-\mathbf {m} _{i}^{(t)}{\big \|}\leq {\big \|}\mathbf {x} _{j}-\mathbf {m} _{i^{*}}^{(t)}{\big \|}\ \forall \ i^{*}=1,\ldots ,k\right\}}$,

– mettre à jour la moyenne de chaque cluster :

${\displaystyle \mathbf {m} _{i}^{(t+1)}={\frac {1}{|S_{i}^{(t)}|}}\sum _{\mathbf {x} _{j}\in S_{i}^{(t)}}\mathbf {x} _{j}}$.

Illustration du déroulement de l'algorithme des k-moyennes

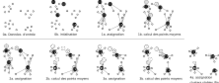
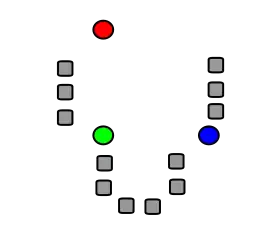
Initialisation

On commence par choisir une valeur pour k ; il est possible d'estimer une valeur pertinente à partir des partitions existantes dans les données^[8].

Une fois le nombre k de valeurs choisi, on procède à leur initialisation. L'initialisation est un facteur déterminant dans la qualité des résultats (minimum local). De nombreux travaux traitent ce point. Il existe deux méthodes d'initialisation habituelles: la méthode de Forgy d'une part et le partitionnement aléatoire d'autre part. La méthode de Forgy affecte les k points des moyennes initiales à k données d'entrée choisies aléatoirement. Le partitionnement aléatoire affecte aléatoirement un cluster à chaque donnée et procède ensuite au (avant-premier) calcul des points de moyennes initiales.

K-moyennes++^[9] est un algorithme d’initialisation des k points qui propose une initialisation améliorant la probabilité d'obtenir la solution optimale (minimum global). L'intuition derrière cette approche consiste à répartir les k points des moyennes initiales. Le point de moyenne initial du premier cluster est choisi aléatoirement parmi les données. Puis chaque point de moyenne initiale est choisi parmi les points restants, avec une probabilité proportionnelle au carré de la distance entre le point et le cluster le plus proche.

Analyse

Il y a un nombre fini de partitions possibles à k classes^[10]. De plus, chaque étape de l'algorithme fait strictement diminuer la fonction de coût, positive, et fait découvrir une meilleure partition. Cela permet d'affirmer que l'algorithme converge toujours en temps fini, c'est-à-dire termine.

Le partitionnement final n'est pas toujours optimal. De plus le temps de calcul peut être exponentiel en le nombre de points, même dans le plan^[11]. Dans la pratique, il est possible d'imposer une limite sur le nombre d’itérations ou un critère sur l'amélioration entre itérations.

À k fixé, la complexité lisse est polynomiale pour certaines configurations, dont des points dans un espace euclidien^[7] et le cas de la divergence de Kullback-Leibler^[12]. Si k fait partie de l'entrée, la complexité lisse est encore polynomiale pour le cas euclidien^[13]. Ces résultats expliquent en partie l'efficacité de l'algorithme en pratique.

Avantages et inconvénients pour l'apprentissage

Un inconvénient possible des k-moyennes pour le partitionnement est que les clusters dépendent de l'initialisation et de la distance choisie.

Le fait de devoir choisir a priori le paramètre k peut être perçu comme un inconvénient ou un avantage. Dans le cas du calcul des sac de mots par exemple, cela permet de fixer exactement la taille du dictionnaire désiré. Au contraire, dans certains partitionnements de données, on préférera s'affranchir d'une telle contrainte.

Quantification vectorielle

Réduction du nombre de couleurs d'une image

Portrait d'Ada Lovelace peint par Alfred Edward Chalon en 1840. L'image non retouchée comprend environ 700 000 pixels qui affichent près de 131 000 couleurs différentes.

L'algorithme des k-moyennes peut être utilisé pour réduire le nombre de couleurs (en) d'une image sans que cela ne nuise trop à sa qualité^[16]. L'espace de couleur du système RGB de codage des couleurs consiste à représenter une couleur par trois nombres entiers compris entre 0 et 255 qui représentent les intensités respectives du rouge, du vert et du bleu dans la couleur à afficher. Cela donne 256³ couleurs possibles, soit environ 16 millions. L'œil humain non-entraîné peine à distinguer autant de couleurs et il est donc possible de remplacer deux couleurs proches par une seule sans grande perte de qualité ; ce peut être utile à des fins de compression ou pour permettre l'affichage optimal d'une image sur un écran ou une imprimante n'offrant pas une grande variété de couleurs. L'algorithme des k-moyennes permet de trouver, pour chaque pixel d'une image, parmi une liste de k couleurs définies, la couleur qui est la plus proche.

Bibliographie

• (en) Richard O. Duda, Peter E. Hart, David G. Stork, Pattern Classification, Wiley-interscience, 2001 (ISBN 0-471-05669-3) [détail des éditions]

Articles connexes

• Partitionnement de données
• k-médoïdes
• k-centre
• k-médiane
• Problème du k-supplier

Liens externes

Implémentations commerciales

• SAS FASTCLUS
• MATLAB : kmeans