Programmation dynamique

En informatique, la programmation dynamique est une méthode algorithmique pour résoudre des problèmes d'optimisation. Le concept a été introduit au début des années 1950 par Richard Bellman^[1]. À l'époque, le terme « programmation » signifie planification et ordonnancement^[1]. La programmation dynamique consiste à résoudre un problème en le décomposant en sous-problèmes, puis à résoudre les sous-problèmes, des plus petits aux plus grands en stockant les résultats intermédiaires. Elle a d'emblée connu un grand succès, car de nombreuses fonctions économiques de l'industrie étaient de ce type, comme la conduite et l'optimisation de procédés chimiques, ou la gestion de stocks^[1].

Principe

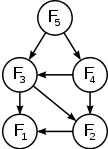
Le graphe de dépendance des sous-problèmes pour le calcul de F₅, le 5ème terme de la suite de Fibonacci.

Illustrons la programmation dynamique sur le calcul du n^ème terme de la suite de Fibonacci, parfois utilisé comme exemple introductif dans un cours sur la programmation dynamique^[2]. La suite de Fibonacci est définie par F₀ = 0, F₁ = 1 et F_n = F_n-1 + F_n-2. La programmation dynamique s'appuie sur le principe d'optimalité de Bellman : une solution optimale d'un problème s'obtient en combinant des solutions optimales à des sous-problèmes. Sur l'exemple de la suite de Fibonacci, la solution F_n s'obtient en additionnant F_n-1 et F_n-2.

La méthode de programmation dynamique, comme la méthode diviser pour régner, résout des problèmes en combinant des solutions de sous-problèmes. Les algorithmes diviser-pour-régner partitionnent le problème en sous-problèmes indépendants qu’ils résolvent récursivement, puis combinent leurs solutions pour résoudre le problème initial. La méthode diviser-pour-régner est inefficace si on doit résoudre plusieurs fois le même sous-problème. Par exemple, l'algorithme suivant est inefficace :

fonction fibonacci(n)
   si n = 0 ou n = 1
         retourner n
   sinon
         retourner fibonacci(n-1) + fibonacci(n-2)

Le graphe de dépendance montré sur la droite n'est pas un arbre : cela illustre que les sous-problèmes se chevauchent. Par exemple, pour calculer F₅, nous avons besoin de F₃ et F₄. Mais pour calculer F₄, nous avons besoin de F₂ et F₃. Ainsi, F₃ est utile à la fois pour le calcul de F₄ et pour le calcul de F₅. La programmation dynamique consiste alors à stocker les valeurs des sous-problèmes pour éviter les recalculs^[3]. Il existe alors deux méthodes pour calculer effectivement une solution : la méthode ascendante et la méthode descendante. Dans la méthode ascendante, on commence par calculer des solutions pour les sous-problèmes les plus petits, puis, de proche en proche, on calcule les solutions des problèmes en utilisant le principe d'optimalité et on mémorise les résultats dans un tableau F[.]. Par exemple :

fonction fibonacci(n)
   F[0] = 0
   F[1] = 1
   pour tout i de 2 à n
        F[i] := F[i-1] + F[i-2]  
   retourner F[n]

Dans la méthode descendante, on écrit un algorithme récursif mais on utilise la mémoïsation pour ne pas résoudre plusieurs fois le même problème, c'est-à-dire que l'on stocke dans un tableau F[.] les résultats des appels récursifs :

fonction fibonacci(n)
   si F[n] n'est pas défini
      si n = 0 ou n = 1
         F[n] := n
      sinon
         F[n] := fibonacci(n-1) + fibonacci(n-2)
   retourner F[n]

La programmation dynamique est utilisée pour résoudre des problèmes d'optimisation. Les sections suivantes en donnent quelques exemples. La conception d’un algorithme de programmation dynamique est typiquement découpée en quatre étapes^[3].

Caractériser la structure d’une solution optimale.
Définir (souvent de manière récursive) la valeur d’une solution optimale.
Calculer la valeur d’une solution optimale.
Construire une solution optimale à partir des informations calculées.

La dernière étape est utile pour calculer une solution optimale, et pas seulement la valeur optimale. Un problème d'optimisation peut avoir de nombreuses solutions. Chaque solution a une valeur, et on souhaite trouver une solution ayant la valeur optimale. Une telle solution optimale au problème n'est pas forcément unique, c'est sa valeur qui l'est.

Exemples

Pyramide de nombres

Dans une pyramide de nombres, on cherche, en partant du sommet de la pyramide, et en se dirigeant vers le bas à chaque étape, à maximiser le total des nombres traversés^[4]. Dans l'exemple ci-dessous, le maximum est obtenu pour le chemin en gras (3+7+4+9 = 23).

Un algorithme naïf, sur l'exemple, consiste à examiner les 8 chemins possibles, et choisir celui qui a le plus grand total. En général, quand la pyramide a n niveaux, il y a $2^{n-1}$ chemins et $2^{n}-2$ calculs à effectuer. Donc l'algorithme naïf est en temps exponentiel en n.

Le paradigme de la programmation dynamique permet d'obtenir un algorithme efficace en définissant des sous-problèmes, en écrivant une relation de récurrence, puis en donnant un algorithme (avec méthode ascendante ou descendante).

Pour toute position $x$ dans la pyramide, notons $v(x)$ le nombre écrit à cette position et $c(x)$ le total des nombres traversés dans un chemin maximal issu de $x$ . Les sous-problèmes consistent à calculer les valeurs de $c(x)$ pour tout $x$ . Le problème initial consiste à calculer $c(x)$ lorsque $x$ est le sommet de la pyramide.

Donnons maintenant une définition récursive de $c(x)$ :

c(x)=v(x)

pour toute position

x

située au rez-de chaussée de la pyramide

c(x)=v(x)+\max(c(g(x)),c(d(x)))

pour toute autre position

x

, où

g(x)

d(x)

sont les positions inférieures gauche et droite sous la position

x

Si on cherche à calculer directement par la définition récursive, on évalue plusieurs fois la même valeur : dans l'exemple ci-dessus, la valeur 4 de la troisième ligne est calculée deux fois en venant de la ligne supérieure (une fois depuis le 7, une fois depuis le 4). Le paradigme de la programmation dynamique consiste à calculer les valeurs $c(x)$ , soit à l'aide d'un algorithme itératif ascendant en stockant les valeurs déjà calculées dans un tableau, soit à l'aide d'un algorithme récursif descendant avec mémoïsation. L'important est de conserver dans un tableau les valeurs intermédiaires. La séquence des calculs est indiquée en gras :

    3                                        23
   7 4                         20  19      20  19
  2 4 6        11 13 15      11  13  15
 9 5 9 3      9  5  9  3

Le nombre de calculs est seulement $n(n-1)/2$ .

Calcul d'un produit de matrices

On se donne des matrices $M_{1},M_{2},\ldots ,M_{h}$ , et on veut calculer la matrice produit $M_{1}M_{2}\cdots M_{h}$ ^[5]^,^[3]. Les matrices ne sont pas forcément carrées, et l'ordre dans lequel on effectue les multiplications peut influencer le coût. Ainsi, le produit des matrices $A_{4\times 5}.B_{5\times 8}.C_{8\times 5}$ exige un nombre de multiplications différent suivant que l'on débute par $(A_{4\times 5}.B_{5\times 8}).C_{8\times 5}=M_{4\times 8}.C_{8\times 5}$ , avec 320 multiplications, ou par $A_{4\times 5}.(B_{5\times 8}.C_{8\times 5})=A_{4\times 5}.N_{5\times 5}$ , avec 300 multiplications. La seconde façon est optimale par rapport au nombre de multiplications.

Si chaque matrice $M_{i}$ a $m_{i}$ lignes et $m_{i+1}$ colonnes, le produit $M_{i-1}M_{i}$ demande $O(m_{i-1}m_{i}m_{i+1})$ opérations. On note $c_{i,j}$ le nombre minimum d'opérations pour calculer le produit $M_{i}\cdots M_{j}$ . On a alors

c_{i,i}=0,c_{i-1,i}=m_{i-1}m_{i}m_{i+1}

Pour obtenir la meilleure valeur pour le produit $M_{i}\cdots M_{j}$ , on le découpe en $M_{i}\cdots M_{k}$ et $M_{k+1}\cdots M_{j}$ et on choisit le meilleur $k$ . Ceci conduit à la formule :

c_{i,j}=\min _{i\leq k<j}[c_{i,k}+c_{k+1,j}+m_{i}m_{k+1}m_{j+1}]

Le calcul des $c_{i,j}$ se fait dans un tableau, diagonale par diagonale, en temps quadratique en le nombre de matrices.

Dans cet exemple aussi, il est important de garder le résultat des calculs dans un tableau pour ne pas les recalculer.

Histoire

Le terme programmation dynamique était utilisé dans les années 1940 par Richard Bellman pour décrire le processus de résolution de problèmes où on trouve les meilleures décisions les unes après les autres. En 1953, il en donne la définition moderne, où les décisions à prendre sont ordonnées par sous-problèmes^[6] et le domaine a alors été reconnu par IEEE comme un sujet d'analyse de systèmes et d’ingénierie. La contribution de Bellman est connu sous le nom d'équation de Bellman, qui présente un problème d'optimisation sous forme récursive.

Bellman explique l'idée du terme programmation dynamique dans son autobiographie, Eye of the Hurricane: An Autobiography ^[7]. Il dit :

« I spent the Fall quarter (of 1950) at RAND. My first task was to find a name for multistage decision processes. An interesting question is, Where did the name, dynamic programming, come from? The 1950s were not good years for mathematical research. We had a very interesting gentleman in Washington named Wilson. He was Secretary of Defense, and he actually had a pathological fear and hatred of the word research. I’m not using the term lightly; I’m using it precisely. His face would suffuse, he would turn red, and he would get violent if people used the term research in his presence. You can imagine how he felt, then, about the term mathematical. The RAND Corporation was employed by the Air Force, and the Air Force had Wilson as its boss, essentially. Hence, I felt I had to do something to shield Wilson and the Air Force from the fact that I was really doing mathematics inside the RAND Corporation. What title, what name, could I choose? In the first place I was interested in planning, in decision making, in thinking. But planning, is not a good word for various reasons. I decided therefore to use the word “programming”. I wanted to get across the idea that this was dynamic, this was multistage, this was time-varying. I thought, let's kill two birds with one stone. Let's take a word that has an absolutely precise meaning, namely dynamic, in the classical physical sense. It also has a very interesting property as an adjective, and that it's impossible to use the word dynamic in a pejorative sense. Try thinking of some combination that will possibly give it a pejorative meaning. It's impossible. Thus, I thought dynamic programming was a good name. It was something not even a Congressman could object to. So I used it as an umbrella for my activities. »

L'adjectif dynamique était donc choisi par Bellman pour insister sur l'aspect temporel des problèmes, et parce que le terme impressionnait^[8]. Le mot programmation référait à l'utilisation d'une méthode pour trouver un programme optimal dans un sens militaire : emploi du temps ou de la logistique. D'ailleurs, l'usage est le même que dans les termes programmation linéaire et programmation mathématique, synonyme pour optimisation mathématique^[9].

Mais cette explication est controversée. Selon le livre Artificial Intelligence: A Modern Approach de Russell et Norvig^[10], l'explication ci-dessus n'est pas tout à fait vraie car le premier article de 1952 où Bellman utilise le terme programmation dynamique a paru avant que Wilson devienne secrétaire de la défense en 1953. Aussi, dans un discours de Harold J. Kushner^[11], il dit de Bellman : « On the other hand, when I asked him the same question, he replied that he was trying to upstage Dantzig's linear programming by adding dynamic. Perhaps both motivations were true. »

Applications algorithmiques

Le problème du plus court chemin (algorithme de Bellman-Ford et algorithme de Floyd-Warshall) ;
Problème d'affectation des ressources. Il s'agit (par exemple) de distribuer m skis à n skieurs (m>n) en minimisant les écarts de taille entre les skis et les skieurs. La propriété d'optimalité des sous-structures (si une distribution est optimale, alors toute sous-partie des skis et des skieurs est optimale) le rend traitable par programmation dynamique ;
Le problème du sac à dos (knapsack en anglais) est un problème classique de recherche opérationnelle qui est NP-difficile, mais qui est résolu de manière pseudo-polynomiale à l'aide d'un algorithme de programmation dynamique ;
Le problème du rendu de monnaie dans le cas général ;
La recherche de la plus longue sous-suite strictement croissante dans une suite de nombres ;
Des problèmes d'algorithmique du texte comme le calcul de la plus longue sous-suite commune entre deux chaînes, le calcul de la distance de Levenshtein ou encore l'alignement de séquences (avec l'algorithme de Smith-Waterman par exemple) ;
L'algorithme CYK est un algorithme d'analyse syntaxique ;
La méthode la plus utilisée pour résoudre le problème de détection de ruptures est la programmation dynamique.

Connexions

La programmation dynamique a des liens avec le calcul des variations et la commande optimale. Un théorème général énonce que tout algorithme de programmation dynamique peut se ramener à la recherche du plus court chemin dans un graphe^[12]. Or, les techniques de recherche heuristique basées sur l'algorithme A* permettent d'exploiter les propriétés spécifiques d'un problème pour gagner en temps de calcul. Autrement dit, il est souvent plus avantageux d'exploiter un algorithme A* que d'utiliser la programmation dynamique.