Matrice (mathématiques)

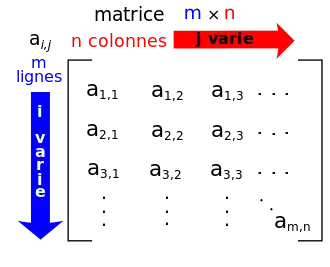
En mathématiques, les matrices sont des tableaux d'éléments (nombres, caractères) qui servent à interpréter en termes calculatoires, et donc opérationnels, les résultats théoriques de l'algèbre linéaire et même de l'algèbre bilinéaire.

Toutes les disciplines étudiant des phénomènes linéaires utilisent les matrices. Quant aux phénomènes non linéaires, on en donne souvent des approximations linéaires, comme en optique géométrique avec les approximations de Gauss.

Historique

Histoire de la notion de matrice

Bien que le calcul matriciel proprement dit n'apparaisse qu'au début du XIX^e siècle, les matrices, en tant que tableaux de nombres, ont une longue histoire d'applications à la résolution d'équations linéaires. Le texte chinois Les Neuf Chapitres sur l'art mathématique, écrit vers le II^e siècle av. J.-C., est le premier exemple connu de l'utilisation de tableaux pour résoudre des systèmes d'équations^[1], introduisant même le concept de déterminant. En 1545, Jérôme Cardan fait connaître cette méthode en Europe en publiant son Ars Magna^[2]. Le mathématicien japonais Seki Kōwa utilise indépendamment les mêmes techniques pour résoudre des systèmes d'équations en 1683^[3]. Aux Pays-Bas, Johan de Witt représente des transformations géométriques à l'aide de tableaux dans son livre de 1659, Elementa curvarum linearum^[2]. Entre 1700 et 1710, Leibniz montre comment utiliser les tableaux pour noter des données ou des solutions, et expérimente plus de 50 systèmes de tableaux à cet effet^[2]. En 1750, Gabriel Cramer publie la règle qui porte son nom^[4].

En 1850, le terme de « matrix » (qui sera traduit par matrice) est forgé (sur la racine latine mater) par James Joseph Sylvester^[5], qui le voit comme un objet donnant naissance à la famille de déterminants actuellement appelés mineurs, c'est-à-dire les déterminants des sous-matrices obtenues en retirant des lignes et des colonnes. Dans un article de 1851, Sylvester précise :

« Dans des articles antérieurs, j'ai appelé matrix un tableau rectangulaire de termes à partir desquels plusieurs systèmes de déterminants peuvent être engendrés, comme issus des entrailles d'un parent commun »^[6].

En 1854, Arthur Cayley publie un traité sur les transformations géométriques utilisant les matrices de façon beaucoup plus générale que tout ce qui a été fait avant lui. Il définit les opérations usuelles du calcul matriciel (addition, multiplication et division) et montre les propriétés d'associativité et de distributivité de la multiplication^[2]. Jusque-là, l'utilisation des matrices s'était essentiellement limitée au calcul des déterminants ; cette approche abstraite des opérations sur les matrices est révolutionnaire. En 1858, Cayley publie son A Memoir on the Theory of Matrices^[7]^,^[8], dans lequel il énonce et démontre le théorème de Cayley-Hamilton^[2] pour les matrices 2×2.

Beaucoup de théorèmes ne sont d'ailleurs démontrés au début que pour de petites matrices : après Cauchy, Hamilton généralise le théorème aux matrices 4×4, et ce n'est qu'en 1898 que Frobenius, étudiant les formes bilinéaires, démontre le théorème en dimension quelconque. C'est aussi à la fin du XIX^e siècle que Wilhelm Jordan établit la méthode d'élimination de Gauss-Jordan (généralisant la méthode de Gauss pour les matrices échelonnées). Au début du XX^e siècle, les matrices occupent une place centrale en algèbre linéaire^[9], en partie grâce au rôle qu'elles jouent dans la classification des systèmes de nombres hypercomplexes du siècle précédent.

Un mathématicien anglais du nom de Cullis est le premier, en 1913, à utiliser la notation moderne des crochets (ou des parenthèses) pour représenter les matrices, ainsi que de la notation systématique $A = [a i, j]$ pour représenter la matrice dont $a i, j$ est le terme de la i-ème ligne et de la j-ème colonne^[2].

La formulation de la mécanique quantique au moyen de la mécanique matricielle, due à Heisenberg, Born et Jordan, amena à étudier des matrices comportant un nombre infini de lignes et de colonnes^[10]. Par la suite, von Neumann précisa les fondements mathématiques de la mécanique quantique, en remplaçant ces matrices par des opérateurs linéaires sur des espaces de Hilbert.

Histoire des déterminants

L'étude théorique des déterminants vient de plusieurs sources^[11]. Des problèmes de théorie des nombres amènent Gauss à relier à des matrices (ou plus précisément à leur déterminant) les coefficients d'une forme quadratique ainsi que les applications linéaires en dimension trois. Gotthold Eisenstein développe ces notions, remarquant en particulier qu'en notation moderne, le produit des matrices est non commutatif. Cauchy est le premier à démontrer des résultats généraux sur les déterminants, en utilisant comme définition du déterminant de la matrice $A = [a i, j]$ le résultat de la substitution, dans le polynôme $a_{1}a_{2}\cdots a_{n}\prod _{i<j}(a_{j}-a_{i})\;$ , des puissances $a k j$ par $a jk$ . Il montre aussi, en 1829, que les valeurs propres d'une matrice symétrique sont réelles^[12]. Jacobi étudie les « déterminants fonctionnels » (appelés par la suite jacobiens par Sylvester), utilisés pour décrire des transformations géométriques d'un point de vue infinitésimal ; les livres Vorlesungen über die Theorie der Determinanten^[13] de Leopold Kronecker et Zur Determinantentheorie^[14] de Karl Weierstrass, tous deux publiés en 1903, définissent pour la première fois les déterminants de manière axiomatique comme formes multilinéaires alternées.

Autres utilisations mathématiques du mot « matrice »

Deux mathématiciens notables au moins ont utilisé le mot dans un sens inhabituel.

Bertrand Russell et Alfred North Whitehead, dans leur Principia Mathematica, utilisent le mot « matrice » dans le cadre de leur axiome de réductibilité (en). Cet axiome permet de réduire le type d'une fonction, les fonctions de type 0 étant identiques à leur extension (en) ; ils appellent « matrice » une fonction n'ayant que des variables libres^[15]. Ainsi, par exemple, une fonction $Φ(x, y)$ de deux variables $x$ et $y$ peut être réduite à une collection de fonctions d'une seule variable, par exemple $y$ , en « considérant » la fonction pour toutes les valeurs $a i$ substituées à la variable $x$ puis réduite à une « matrice » de valeurs en procédant de même pour $y$ : $\forall b j, \forall a i, Φ(a i, b j)$ .

Alfred Tarski, dans son Introduction à la logique de 1946, utilise le mot « matrice » comme un synonyme de table de vérité^[16].

Définitions

Une matrice à $m$ lignes et $n$ colonnes est un tableau rectangulaire de $m \times n$ nombres, rangés ligne par ligne. Il y a $m$ lignes, et dans chaque ligne $n$ éléments.

Plus formellement et plus généralement, soient $I$ , $J$ et $K$ trois ensembles ( $K$ sera souvent muni d'une structure d'anneau ou même de corps commutatif).

Une matrice de type $(I, J)$ ^[17] à coefficients dans $K$ , est une famille d'éléments de $K$ indexée par le produit cartésien $I \times J$ , c'est-à-dire une application $A$ de $I \times J$ dans $K$ . Son type (I,J) fait partie de la spécification de la matrice, mais pas l'ensemble $K$ (par exemple une matrice à coefficients réels est aussi une matrice à coefficients complexes).

Le plus souvent, comme dans toute la suite de cet article, les ensembles $I$ et $J$ sont finis et sont respectivement les ensembles de nombres entiers ${1, \dots, m}$ et ${1, \dots, n}$ . Dans ce cas, on dit que la matrice a $m$ lignes et $n$ colonnes, ou qu'elle est de dimension ou taille $(m, n)$ . En notant $a i, j$ l'image d'un couple $(i, j)$ par l'application $A$ , la matrice peut alors être notée

A=(a_{i,j})_{1\leq i\leq m,1\leq j\leq n}

ou plus simplement $(a i, j)$ si le contexte s'y prête.

Dans le cas particulier où $I$ ou $J$ est l'ensemble vide, la matrice correspondante est appelée la matrice vide de type (I,J). Il est nécessaire de distinguer les matrices vides de différents types pour définir le produit matriciel, car le produit de matrices (vides) de tailles respectives $(m,0)$ et $(0, n)$ est une matrice (nulle, mais non vide) de taille $(m, n)$ , et dépend donc des entiers m, n.

On représente généralement une matrice sous la forme d'un tableau rectangulaire. Par exemple, est représentée ci-dessous une matrice $A$ , à coefficients entiers, et de dimension (3,4) :

A={\begin{pmatrix}0&1&2&3\\4&5&6&7\\8&9&10&11\\\end{pmatrix}}

Dans cette représentation, le premier coefficient de la dimension est le nombre de lignes, et le deuxième, le nombre de colonnes du tableau. Une matrice pour laquelle le nombre $m$ de lignes est égal au nombre $n$ de colonnes sera dite matrice carrée de taille (ou d’ordre) $n$ . Une matrice ne comportant qu'une seule ligne et $n$ colonnes est appelée matrice ligne (ou plus souvent vecteur ligne) de taille $n$ . Une matrice comportant $m$ lignes et une seule colonne est appelée matrice colonne (ou plus souvent vecteur colonne) de taille $m$ .

Pour repérer un coefficient d'une matrice, on indique son indice de ligne puis son indice de colonne, les lignes se comptant du haut vers le bas et les colonnes de la gauche vers la droite. Par exemple, on notera $a i, j$ , les coefficients de la matrice $A$ , $i$ compris entre 1 et 3 désignant le numéro de la ligne sur laquelle figure le coefficient envisagé, et $j$ compris entre 1 et 4 désignant son numéro de colonne ; ainsi $a 2,4 = 7$ .

La disposition générale des coefficients d'une matrice $A$ de taille $(m, n)$ est donc la suivante

A={\begin{pmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{m,1}&a_{m,2}&\cdots &a_{m,n}\\\end{pmatrix}}

Les coefficients $a i, j$ avec $i = j$ sont dits diagonaux, ceux avec $i \neq j$ sont dits extradiagonaux.

Une sous-matrice de $A$ est une matrice obtenue en sélectionnant une partie $I \subset {1,..., m}$ de ses lignes et une partie $J \subset {1,..., n}$ de ses colonnes ; on la note $A I, J$ . On dit qu'une sous-matrice est principale si $I = J$ dans la définition précédente. La diagonale principale de $A$ est le vecteur

\operatorname {diag} (A):={\begin{pmatrix}a_{1,1}\\a_{2,2}\\\vdots \\a_{p,p}\end{pmatrix}},

où $p = min(m, n)$ .

Pour effectuer certaines opérations, il peut être utile de travailler sur le système des lignes ou des colonnes d'une matrice. On pourra alors l'écrire sous une des formes suivantes

A={\begin{pmatrix}L_{1}\\L_{2}\\\vdots \\L_{m}\\\end{pmatrix}}\quad {\text{  ou  }}\quad A={\begin{pmatrix}C_{1}&C_{2}&\dots &C_{n}\\\end{pmatrix}}.

L'ensemble des matrices à coefficients dans $K$ possédant $m$ lignes et $n$ colonnes est noté $M m, n (K)$ (ou parfois $M (m, n, K)$ ).

Lorsque $m = n$ on note plus simplement $M n (K)$ .

Soit $K$ un ensemble et $A = (a i, j) 1 \leq i \leq m, 1 \leq j \leq n \in M m, n (K)$ ; on appelle matrice transposée de $A$ la matrice $A T = (a j, i) 1 \leq j \leq n, 1 \leq i \leq m \in M n, m (K)$ . Si $K$ est un magma, $A T = (a j, i) 1 \leq j \leq n, 1 \leq i \leq m \in M n, m (K op)$ où $K op$ est le magma opposé de $K$ .

Par exemple, avec la matrice $A$ des exemples précédents, on a

A^{\mathsf {T}}={\begin{pmatrix}0&4&8\\1&5&9\\2&6&10\\3&7&11\\\end{pmatrix}}.

Espaces de matrices

On suppose maintenant que $K$ est muni d'une structure d'anneau ; les éléments de $K$ seront appelés scalaires, par opposition aux matrices dont nous allons voir qu'elles peuvent être considérées comme des vecteurs.

Addition des matrices et multiplication par un scalaire

On définit sur $M m, n (K)$ une loi de composition interne provenant de l'addition des scalaires :

(a_{i,j})+(b_{i,j})=(c_{i,j}),\ {\textrm {avec}}\ c_{i,j}=a_{i,j}+b_{i,j}

On ne peut additionner que deux matrices de même taille.

Exemple :

{\begin{array}{l}{\begin{pmatrix}0&1&2&3\\4&5&6&7\\\end{pmatrix}}+{\begin{pmatrix}0&0&1&1\\0&1&0&1\\\end{pmatrix}}={\begin{pmatrix}0&1&3&4\\4&6&6&8\\\end{pmatrix}}\end{array}}

Pour chaque valeur du couple $(m, n)$ , l'espace $M m, n (K)$ devient alors un groupe abélien, d'élément neutre la matrice nulle, celle dont tous les coefficients valent 0.

On définit aussi une opération à droite de $K$ sur chaque espace $M m, n (K)$ en associant, à chaque scalaire $λ$ dans $K$ et à chaque matrice $(a i, j)$ à coefficients dans $K$ , la matrice $(a i, j) λ = (a i, j λ)$ obtenue en effectuant la multiplication à droite, dans $K$ , de tous les coefficients de la matrice initiale par $λ$ : c'est la multiplication par un scalaire. Lorsque l'anneau est commutatif, la multiplication peut également s'effectuer à gauche.

En reprenant toujours la matrice $A$ du premier exemple (voir supra) :

2A={\begin{pmatrix}0&2&4&6\\8&10&12&14\\16&18&20&22\\\end{pmatrix}}

Les espaces $M m, n (K)$ ainsi obtenus ont donc une structure de $K$ -module à droite, et plus particulièrement de $K$ -espace vectoriel, si $K$ est un corps commutatif.

Base canonique de l'espace des matrices

Le $K$ -module $M m, n (K)$ est libre de rang $mn$ , c'est-à-dire qu'il possède une base de $mn$ éléments : il suffit de considérer la base canonique $(E i, j) 1 \leq i \leq m, 1 \leq j \leq n$ . La matrice $E i, j$ est celle dont tous les coefficients sont nuls sauf celui d'indice $(i, j)$ , qui vaut 1.

Les coordonnées dans la base canonique d'une matrice $A$ sont ses coefficients :

A=\sum _{1\leqslant i\leqslant m \atop 1\leqslant j\leqslant n}a_{i,j}E_{i,j}

Exemple :

${\begin{pmatrix}0&1&2\\4&3&1\\\end{pmatrix}}=0\cdot {\begin{pmatrix}1&0&0\\0&0&0\\\end{pmatrix}}+1\cdot {\begin{pmatrix}0&1&0\\0&0&0\\\end{pmatrix}}+2\cdot {\begin{pmatrix}0&0&1\\0&0&0\\\end{pmatrix}}+4\cdot {\begin{pmatrix}0&0&0\\1&0&0\\\end{pmatrix}}+3\cdot {\begin{pmatrix}0&0&0\\0&1&0\\\end{pmatrix}}+1\cdot {\begin{pmatrix}0&0&0\\0&0&1\\\end{pmatrix}}$

Produit matriciel

On commence par définir le produit d'une matrice ligne par une matrice colonne^[18]^,^[19]. Soit $n$ un nombre entier, $L$ une matrice ligne, $x i$ ses coefficients, $C$ une matrice colonne, $y i$ ses coefficients. On les suppose toutes deux de taille $n$ . On définit alors le produit, considéré comme un scalaire ou une matrice de dimension (1, 1) :

LC={\begin{pmatrix}x_{1}&\dots &x_{n}\end{pmatrix}}{\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}}=\sum _{1\leq i\leq n}x_{i}y_{i}

On remarque la condition de compatibilité sur les tailles des matrices (égalité du nombre de colonnes de la première avec le nombre de lignes de la deuxième). On définit maintenant plus généralement un produit entre deux matrices, la première, $(x i, j)$ dans $M m, n (K)$ , la deuxième, $(y i, j)$ dans $M n, p (K)$ , toujours avec une condition de compatibilité sur les tailles (et l'ordre des facteurs de la multiplication ne peut en général pas être changé). Le résultat obtenu est une matrice de $M m, p (K)$ , dont les coefficients $(z i, j)$ sont obtenus par :

z_{i,j}=\sum _{1\leq k\leq n}x_{i,k}y_{k,j}=x_{i,1}y_{1,j}+x_{i,2}y_{2,j}+\cdots +x_{i,n}y_{n,j}

À la lumière de l'exemple de la multiplication d'une matrice ligne par une matrice colonne, on peut reformuler cette définition en disant que ce coefficient est égal au produit de la ligne i de la première matrice par la colonne j de la deuxième, ce qui s'écrit de la manière suivante, si les $L i$ sont les lignes de la première matrice, et les $C j$ les colonnes de la deuxième, le produit est : ${\begin{pmatrix}L_{1}\\\vdots \\L_{m}\end{pmatrix}}{\begin{pmatrix}C_{1}&\dots &C_{p}\end{pmatrix}}={\begin{pmatrix}L_{1}C_{1}&L_{1}C_{2}&\dots &L_{1}C_{p}\\L_{2}C_{1}&L_{2}C_{2}&\dots &L_{2}C_{p}\\\vdots &\vdots &\ddots &\vdots \\L_{m}C_{1}&L_{m}C_{2}&\dots &L_{m}C_{p}\\\end{pmatrix}}$ .

Le produit matriciel est associatif, distributif à droite et à gauche par rapport à l'addition matricielle. En revanche, même lorsque les dimensions permettent de donner un sens à la question et même si l'anneau des scalaires est commutatif, un produit de matrices ne commute en général pas : $AB$ n'est pas en général égal à $BA$ , par exemple :

A={\begin{pmatrix}0&0\\1&0\end{pmatrix}}\quad B={\begin{pmatrix}1&0\\0&0\\\end{pmatrix}}\quad AB={\begin{pmatrix}0&0\\1&0\\\end{pmatrix}}\quad BA={\begin{pmatrix}0&0\\0&0\\\end{pmatrix}}.

Remarque : le produit de deux matrices non nulles peut être nul, comme ci-dessus ; on dit que l'anneau des matrices n'est pas intègre.

Il arrive même, selon les tailles respectives des matrices $A$ et B, que l'un des deux produits existe et pas l'autre.

La transposition et le produit matriciel sont compatibles au sens suivant :

\forall A\in M_{n,p}(K),\ \forall B\in M_{p,q}(K),\ (AB)^{\mathsf {T}}=B^{\mathsf {T}}\cdot A^{\mathsf {T}}

(même si l'anneau $K$ n'est pas commutatif, en se rappelant que les matrices transposées ont leurs coefficients dans l'anneau opposé $K op$ ).

Matrice identité et inverse d'une matrice

Pour chaque nombre entier n, on note I_n la matrice carrée de taille n dont les coefficients diagonaux sont égaux à 1 et dont les autres coefficients sont nuls ; elle est appelée matrice identité de taille n.

I_{1}={\begin{pmatrix}1\end{pmatrix}}\quad I_{2}={\begin{pmatrix}1&0\\0&1\end{pmatrix}}\quad I_{3}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}\quad I_{n}=(\delta _{i,j})_{1\leq i\leq n,1\leq j\leq n}

où δ_i,j désigne le symbole de Kronecker.

Sous réserve de compatibilité des tailles, les matrices I_n sont neutres à droite et à gauche pour la multiplication.

\forall A\in M_{m,n}(K),\ I_{m}\,A=A\,I_{n}=A.

Soit $A$ une matrice de dimension (m, n). On dit que $A$ est inversible à droite (respectivement à gauche) s'il existe une matrice B de taille (n, m) telle que $AB = I m$ (respectivement $BA = I n$ ). Elle est simplement dite inversible si elle l'est à la fois à droite et à gauche. Le sous-ensemble de $M n (K)$ constitué des matrices inversibles possède une structure de groupe pour le produit matriciel ; il est appelé groupe linéaire et noté $GL n (K)$ .

Pour une matrice carrée à coefficients dans un anneau commutatif $K$ , être inversible à droite ou à gauche ou avoir un déterminant inversible dans $K$ (c'est-à-dire non nul si $K$ est un corps) sont trois propriétés équivalentes.

Algèbre des matrices carrées

Lorsque l'anneau $K$ est commutatif, l'ensemble $M n (K)$ des matrices carrées de taille n est donc muni d'une structure de $K$ -algèbre associative et unitaire avec l'addition matricielle, le produit par un scalaire et le produit matriciel.

On appelle matrice scalaire une matrice de la forme $I n λ$ où $λ$ est un élément de l'anneau $K$ .

I_{n}a={\begin{pmatrix}a&0&\dots &0\\0&a&\dots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\dots &a\end{pmatrix}}

Ces matrices s'appellent matrices scalaires car elles se comportent comme des scalaires, vis-à-vis de la multiplication :

\forall \lambda \in K,\ \forall A\in M_{n}(K),\ A(I_{n}\lambda )=A\lambda ~.

Lorsque $K$ est commutatif, ou à défaut, lorsque $λ$ est central dans $K$ , c'est-à-dire lorsque $λ$ commute avec tous les éléments de $K$ , on a en outre :

\forall \lambda \in K,\ \forall A\in M_{n}(K),(\lambda I_{n})\ A=A\lambda ~.

Réciproquement, toute matrice $B$ de $M n (K)$ telle que $\forall A \in M n (K), AB = BA$ est une matrice scalaire $I n λ$ où $λ$ est central dans $K$ (ceci se démontre en prenant pour $A$ les matrices de la base canonique).

Une matrice de la forme :

{\begin{pmatrix}a_{1}&0&\dots &0\\0&a_{2}&\dots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\dots &a_{n}\end{pmatrix}}

sera dite matrice diagonale.

Outre le déterminant, une autre fonction à noter est la trace. Toutes deux apparaissent dans un objet plus général, le polynôme caractéristique, qui à son tour permet d'obtenir certaines caractérisations des matrices diagonalisables (c'est-à-dire semblables à une matrice diagonale), ou de la trigonalisation.

Actions du groupe linéaire

Il existe plusieurs manières de faire agir le groupe linéaire $GL n (K)$ sur les espaces de matrices, notamment :

action par multiplication à gauche de $GL m (K)$ sur $M m, n (K)$ , qui à $P$ et $A$ , associe $PA$ ,
action (à gauche) par multiplication à droite de $GL n (K)$ sur $M m, n (K)$ , qui à $Q \in GL n (K)$ et $A \in M m, n (K)$ , associe $AQ -1$ ,
action par conjugaison de $GL n (K)$ sur $M n (K)$ , qui à $P \in GL n (K)$ et $A \in M n (K)$ , associe $PAP -1$ .

On décrit maintenant les résultats classiques sur ces actions, lorsque les scalaires forment un corps commutatif. Les deux premières actions sont souvent considérées simultanément ; on s'intéresse donc à la question : deux matrices $A$ et $B$ de dimension $(m, n)$ étant données, existe-t-il des matrices $P \in GL m (K)$ et $Q \in GL m (K)$ telles que $A = PBQ -1$ ? Si tel est le cas, les deux matrices $A$ et $B$ sont dites équivalentes. Le résultat principal est que deux matrices sont équivalentes si et seulement si elles ont même rang, ce qui s'exprime encore en disant que le rang est un invariant complet pour les doubles classes définies par les deux actions de multiplication à gauche et à droite. Par ailleurs, une matrice étant donnée, on peut trouver d'autres matrices privilégiées (les matrices échelonnées) dans la même orbite pour une de ces actions par la méthode du pivot de Gauss.

Pour l'action par conjugaison, deux matrices carrées $A$ et $B$ de taille $n$ dans la même orbite admettent une relation de la forme $A = PBP -1$ , pour une certaine matrice $P$ inversible de taille $n$ ; deux telles matrices sont dites semblables. La description d'un système complet d'invariants (caractérisant des matrices semblables) est plus délicate. On appelle ces invariants les invariants de similitude. D'un point de vue algorithmique, la réduction d'une matrice quelconque à une matrice sous une forme privilégiée se fait par un algorithme inspiré de celui du pivot de Gauss, voir théorème des facteurs invariants.

Interprétations linéaires

Un intérêt principal des matrices est qu'elles permettent d'écrire commodément les opérations habituelles de l'algèbre linéaire, avec une certaine canonicité.

Coordonnées

Le premier point est de remarquer que le $K$ -module Kⁿ s'identifie canoniquement à l'espace de matrices colonne $M n,1 (K)$ : si $e i$ est le n-uplet de $K n$ dont tous les coefficients sont nuls, sauf le i-ème qui vaut 1, on lui associe la i-ème matrice colonne $E i,1$ de la base canonique de $M n,1 (K)$ (celle dont tous les coefficients sont nuls sauf le i-ème qui vaut 1), et on étend l'identification par linéarité ; la matrice associée à chaque n-uplet sera appelée matrice coordonnée canonique.

D'autres identifications sont cependant possibles ; lorsqu'on peut parler de base (si l'anneau des scalaires est un corps, par exemple), on peut associer les matrices colonnes élémentaires à n'importe quelle base de l'espace $K n$ (ou plus généralement d'un $K$ -module libre), puis à nouveau étendre par linéarité ; les matrices associées seront appelées matrices coordonnées dans la base envisagée.

On peut juxtaposer les matrices coordonnées, dans une base fixée, de plusieurs n-uplets. On obtient ainsi la matrice coordonnée d'une famille de vecteurs. Le rang de la matrice est alors défini comme la dimension de la famille de ces vecteurs. En particulier la matrice d'une base dans une autre base est appelée matrice de passage entre ces deux bases, ou matrice de changement de base. Si X et X' sont les matrices coordonnées du même vecteur dans deux bases $B$ et C, et que P est la matrice de passage de la base C dans la base $B$ , on a la relation (une matrice de passage est toujours inversible) :

X=PX'\quad X'=P^{-1}X

Applications linéaires

Soient E et F deux espaces vectoriels de dimensions respectives n et m sur un corps commutatif^[20] $K$ , B une base de E, C une base de F et φ une application linéaire de E dans F.

On appelle matrice de φ dans le couple de bases (B, C) la matrice $mat B, C (φ)$ de $M m, n (K)$ telle que pour tout vecteur $x$ de $E$ , si l'on note $y = φ (x)$ , $X = mat B (x)$ et $Y = mat C (y)$ , alors :

Y={\textrm {mat}}_{B,C}(\varphi )\times X.

Si ψ est une deuxième application linéaire, de F dans un troisième espace vectoriel G de base D, alors, relativement aux bases $B$ , C, D, la matrice de la composée $ψ \circ φ$ est égale au produit des matrices de $ψ$ et $φ$ . Plus précisément :

{\textrm {mat}}_{B,D}(\psi \circ \varphi )={\textrm {mat}}_{C,D}(\psi )\times {\textrm {mat}}_{B,C}(\varphi ).

L'application de L(E, F) dans $M m, n (K)$ qui à chaque $φ$ associe sa matrice dans (B, C) est un isomorphisme d'espaces vectoriels.

Pour toute matrice $M$ de $M m, n (K)$ , l'application X ↦ MX du $K$ -espace vectoriel M_n,1(K) dans le $K$ -espace vectoriel M_m,1(K) est linéaire. C'est un point clef du lien entre algèbre linéaire et matrices. En conséquence, il arrive souvent que l'on identifie la matrice $M$ avec cette application linéaire. On parlera alors de noyau de la matrice, d'espaces propres de la matrice, d'image de la matrice, etc.

Si $B$ et $B'$ sont deux bases de E, C et C' deux bases de F, P = mat_B(B') la matrice de passage de $B$ vers $B'$ et Q la matrice de passage de C vers C', alors les deux matrices M et M' d'une même application linéaire de E dans F, dans les couples de bases (B, C) et (B', C'), sont liées par : M' = Q⁻¹MP. On constate ainsi que deux matrices équivalentes sont deux matrices qui représentent la même application linéaire dans des bases différentes. En particulier, dans le cas d'un endomorphisme, si l'on impose $B = C$ et $B' = C'$ , la formule précédente devient : M' = P⁻¹MP et deux matrices semblables sont deux matrices qui représentent le même endomorphisme dans des bases différentes.

Transposition

Soient de nouveau E et F deux $K$ -espaces vectoriels de dimensions finies^[20], de bases respectives $B$ et C, et φ une application linéaire de E dans F. L'application linéaire transposée ^tφ : F* → E* entre leurs duals est définie par

\forall y^{*}\in F^{*},\forall x\in E,\quad \left\langle ^{\operatorname {t} }\!\varphi \left(y^{*}\right),x\right\rangle =\left\langle y^{*},\varphi \left(x\right)\right\rangle .

Sa matrice dans le couple de bases duales (C*, B*) est liée à celle de φ dans (B, C) par :

{\textrm {mat}}_{C^{*},B^{*}}(^{\operatorname {t} }\!\varphi )={}^{\operatorname {t} }\!({\textrm {mat}}_{B,C}(\varphi )).

Remarque

Lorsque l'anneau n'est pas commutatif, si l'on représente les vecteurs par des matrices colonne, l'algèbre linéaire n'est compatible avec le calcul matriciel que si les modules ou espaces vectoriels considérés sont à droite, comme dans les articles détaillés signalés ci-dessus, une application linéaire correspondant à la multiplication à gauche d'un vecteur colonne par la matrice qui la représente. Si l'on tient à avoir des modules ou espaces vectoriels à gauche, il faut représenter les vecteurs par des matrices ligne, une application linéaire étant cette fois représentée par la multiplication à droite d'un vecteur ligne par la matrice qui la représente^[21].

Systèmes d'équations linéaires

En général, un système de m équations linéaires à n inconnues peut être écrit sous la forme suivante :

\left\{{\begin{matrix}a_{1,1}x_{1}+a_{1,2}x_{2}+...+a_{1,n}x_{n}=b_{1}\\a_{2,1}x_{1}+a_{2,2}x_{2}+...+a_{2,n}x_{n}=b_{2}\\\vdots \\\vdots \\a_{m,1}x_{1}+a_{m,2}x_{2}+...+a_{m,n}x_{n}=b_{m}\end{matrix}}\right.

où $x 1, ..., x n$ sont les inconnues et les nombres $a i, j$ sont les coefficients du système.

Ce système peut s'écrire sous la forme matricielle :

Ax=b

avec :

A={\begin{pmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{m,1}&a_{m,2}&\cdots &a_{m,n}\end{pmatrix}};\qquad x={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}\quad {\text{et}}\quad b={\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{pmatrix}};

la théorie de la résolution des systèmes utilise les invariants liés à la matrice $A$ (appelée matrice du système), par exemple son rang, et, dans le cas où $A$ est inversible, son déterminant (voir l'article règle de Cramer).

Interprétations bilinéaires

Dans ce paragraphe, l'anneau $K$ des scalaires sera supposé commutatif. Dans la plupart des applications, ce sera un corps commutatif.

Le cas non commutatif existe aussi mais il faut prendre quelques précautions et les notations deviennent trop lourdes pour cet article.

Matrice d'une forme bilinéaire

Soient E un $K$ -module libre et B = (e₁, … , e_n) une base de E.

Soit $f:E\times E\to K$ une forme bilinéaire. On définit la matrice de $f$ dans la base B par la formule suivante :

{\textrm {mat}}_{B}\,f=(f(e_{i},e_{j}))_{1\leq i\leq n,\ 1\leq j\leq n}={\begin{pmatrix}f(e_{1},e_{1})&f(e_{1},e_{2})&\dots &f(e_{1},e_{n})\\f(e_{2},e_{1})&f(e_{2},e_{2})&\dots &f(e_{2},e_{n})\\\vdots &\vdots &\ddots &\vdots \\f(e_{n},e_{1})&f(e_{n},e_{2})&\dots &f(e_{n},e_{n})\\\end{pmatrix}}

Dans le cas particulier où K = ℝ et $f$ est un produit scalaire, cette matrice est appelée matrice de Gram.

La matrice $mat B f$ est symétrique (respectivement antisymétrique) si et seulement si la forme bilinéaire $f$ est symétrique (respectivement antisymétrique).

Soient $x$ et $y$ deux vecteurs de E. Notons $X$ et $Y$ leurs coordonnées dans la base B et $A = mat B f$ . On a alors la formule : $f(x,y)={}^{\operatorname {t} }\!X~A~Y$ .

Deux formes bilinéaires sont égales si et seulement si elles ont la même matrice dans une base donnée.

Matrice d'une forme quadratique

Lorsque $K$ est un corps de caractéristique différente de 2, on appelle matrice d'une forme quadratique la matrice de la forme bilinéaire symétrique dont est issue la forme quadratique.

Formule de changement de base

Soient E un $K$ -module libre et B, C deux bases de E. Soit $f:E\times E\to K$ une forme bilinéaire.

Notons $M = mat B f$ la matrice de $f$ dans la base B et $M' = mat C f$ la matrice de $f$ dans la base C. Notons $P = mat B C$ la matrice de passage. On a alors la formule de changement de base pour une forme bilinéaire (à ne pas confondre avec celle pour une application linéaire) :

M'={}^{\operatorname {t} }\!P~M~P

Matrices congruentes

Deux matrices carrées $A$ et $B$ sont dites congruentes s'il existe une matrice inversible $P$ telle que

A={}^{\operatorname {t} }\!P~B~P~.

Deux matrices congruentes sont deux matrices qui représentent la même forme bilinéaire dans deux bases différentes.

Lorsque $K$ est un corps de caractéristique différente de 2, toute matrice symétrique est congruente à une matrice diagonale. L'algorithme utilisé s'appelle réduction de Gauss à ne pas confondre avec le pivot de Gauss.

Catalogue partiel

Une matrice est dite symétrique si elle est égale à sa transposée et antisymétrique si elle est opposée à sa transposée.

Une matrice $A$ à coefficients complexes est dite hermitienne si elle est égale à la transposée de sa matrice conjuguée $A$ .

Une matrice $A$ est dite

orthogonale si elle est à coefficient réels et si $t A A = A t A = I$ ,
unitaire si elle est à coefficients complexes et si $t A A = A t A = I$

(Pour plus d'exemples, voir en bas de page : « Articles connexes » et palette « Matrices »)

Décomposition d'une matrice

On utilise abusivement le terme décomposition d'une matrice, qu'il s'agisse d'une véritable décomposition (en somme) comme dans la décomposition de Dunford ou d'une factorisation comme dans la plupart des autres décompositions.

Réduction d'une matrice carrée

Réduire une matrice, c'est trouver une matrice qui lui est semblable la plus simple possible.
Une matrice diagonalisable est une matrice semblable à une matrice diagonale : $A$ est diagonalisable s'il existe une matrice inversible $P$ et une matrice diagonale $D$ telles que $A = P -1 DP$ .
Sur un corps algébriquement clos, on dispose de la réduction de Jordan qui est optimale et il existe des décompositions intermédiaires comme la décomposition de Dunford qui utilise les sous-espaces caractéristiques ou celle de Frobenius qui utilise les sous-espaces cycliques.
Les polynômes d'endomorphismes jouent un rôle crucial dans les techniques de réduction.

Décomposition LU

C'est une factorisation en produit de deux matrices triangulaires.
En lien avec le pivot de Gauss, c'est une méthode qui permet d'inverser une matrice.

Décomposition QR

C'est un résultat sur les matrices à coefficients réels ou à coefficients complexes.
C'est une factorisation en produit d'une matrice orthogonale et d'une matrice triangulaire.
C'est une traduction matricielle du procédé de Gram-Schmidt.

Décomposition polaire

C'est un résultat sur les matrices à coefficients réels ou à coefficients complexes.
C'est une factorisation en produit d'une matrice orthogonale et d'une matrice symétrique définie positive dans le cas réel, en produit d'une matrice unitaire et d'une matrice hermitienne définie positive dans le cas complexe.
On peut décomposer à droite ou à gauche.
On a unicité de la factorisation pour les matrices inversibles.

Normes

Normes d'algèbre

Dans tout ce paragraphe, $K = ℝ$ ou $ℂ$ .

Une norme matricielle est une norme d'algèbre sur l'algèbre $M n (K)$ , c'est-à-dire une norme d'espace vectoriel qui est de plus sous-multiplicative.

Le rayon spectral d'une matrice carrée $A$ à coefficients complexes est le plus grand module de ses valeurs propres. Il est égal à la borne inférieure des normes matricielles de $A$ .

Sur $M n (K)$ , toute norme $N$ subordonnée à une norme sur $K n$ est une norme d'algèbre vérifiant de plus $N (I n) = 1$ (la réciproque est fausse).

Structure d'espace vectoriel euclidien

L'espace vectoriel $M m, n (ℝ)$ , canoniquement isomorphe à $ℝ mn$ , hérite de sa structure euclidienne. Le produit scalaire se transcrit en

${\displaystyle (A,B)\in M_{m,n}(\mathbb {R} )\times M_{m,n}(\mathbb {R} )\mapsto \langle A,B\rangle$

où $\operatorname {tr}$ désigne la trace (i.e., $\textstyle \operatorname {tr} \,M=\sum _{i=1}^{n}m_{ii}$ ) et les $a i, j$ (resp. $b i, j$ ) désignent les éléments de $A$ (resp. $B$ ). La norme associée à ce produit scalaire est la norme de Frobenius ou norme de Hilbert-Schmidt :

\|A\|_{F}=\left(\sum _{1\leq i\leq m \atop 1\leq j\leq n}a_{i,j}^{2}\right)^{\frac {1}{2}}=\|\sigma (A)\|_{2},

où $σ (A)$ est le vecteur des valeurs singulières de $A$ et $\|\cdot \|_{2}$ est la norme euclidienne.

Si $m = n > 1$ , il ne s'agit pas d'une norme subordonnée, puisque $\|I_{n}\|_{F}={\sqrt {n}}\neq 1.$

L'inégalité de Cauchy-Schwarz s'écrit (comme pour tout produit scalaire) :

\forall A,B\in \mathbb {R} ^{m\times n},\langle A,B\rangle \leqslant \|A\|_{F}\,\|B\|_{F}.

Cette inégalité peut être renforcée par l'inégalité de trace de von Neumann^[22] :

\forall A,B\in \mathbb {R} ^{m\times n},\langle A,B\rangle \leqslant \sigma (A)^{\mathsf {T}}\sigma (B),

où $σ (A)$ est le vecteur des valeurs singulières de $A$ , rangées en ordre décroissant. Elle a la même structure que l'inégalité de Ky Fan, laquelle suppose que les matrices sont carrées et symétriques (on peut alors remplacer $σ (•)$ par le vecteur des valeurs propres).

L'espace vectoriel $M m,n (ℂ)$ est muni d'une structure similaire d'espace hermitien.

Exponentielle d'une matrice

Soit $A \in M n (ℂ)$ , soit $N$ une norme d'algèbre et $\sum a_{n}z^{n}$ une série entière de rayon de convergence $R$ .

Alors si $N (A) < R$ , la série $\sum a_{n}A^{n}$ est absolument convergente. (On le montre en utilisant que $N (A n) \leq N (A) n$ .)

En particulier, on peut définir, pour toute matrice carrée complexe, la quantité

\exp(A)=\sum _{k=0}^{+\infty }{\frac {1}{k!}}A^{k}

Le calcul effectif de cette exponentielle se fait par réduction de la matrice.

L'exponentielle joue un rôle central dans l'étude des systèmes linéaires d'équations différentielles.

Notes et références

↑ Chapitre 8 : Fang cheng - La disposition rectangulaire : problèmes à plusieurs inconnues, résolus selon un principe similaire à l'élimination de Gauss.
1 2 3 4 5 6 (en) Discrete Mathematics 4th Ed. Dossey, Otto, Spense, Vanden Eynden, Addison Wesley, 10 octobre 2001, (ISBN 978-0321079121) (pages 564-565).
↑ (en) Joseph Needham et Wang Ling, Science and Civilisation in China, vol. III, Cambridge, Cambridge University Press, 1959, 877 p. (ISBN 978-0-521-05801-8, lire en ligne), p. 117.
↑ Gabriel Cramer, Introduction à l'Analyse des lignes courbes algébriques, Genève, Europeana, 1750 (lire en ligne), p. 656–659.
↑ De nombreuses sources affirment qu'il l'aurait fait en 1848, mais Sylvester n'a rien publié cette année-là. (voir The Collected Mathematical Papers of James Joseph Sylvester (Cambridge, England: Cambridge University Press, 1904), vol. 1.). Sa première utilisation du terme matrix, en 1850, figure dans Additions to the articles in the September number of this journal, “On a new class of theorems,” and on Pascal's theorem, The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science, 37 : 363-370. (1850), page 369 : « For this purpose we must commence, not with a square, but with an oblong arrangement of terms consisting, suppose, of m lines and n columns. This will not in itself represent a determinant, but is, as it were, a Matrix out of which we may form various systems of determinants […] ».
↑ « I have in previous papers defined a “Matrix” as a rectangular array of terms, out of which different systems of determinants may be engendered as from the womb of a common parent » dans The Collected Mathematical Papers of James Joseph Sylvester : 1837–1853, Article 37, p. 247.
↑ Phil. Trans. 1858, vol. 148, pp. 17-37 Math. Papers II 475-496.
↑ Jean Dieudonné, Abrégé d'histoire des mathématiques 1700-1900, Paris, FR, Hermann, 1978.
↑ (en) Maxime Bôcher, Introduction to Higher Algebra, New York, NY, Dover Publications, 2004, 321 p. (ISBN 978-0-486-49570-5).
↑ (en) Jagdish Mehra et Helmut Rechenberg, The Historical Development of Quantum Theory, Berlin, DE; New York, NY, Springer-Verlag, 1987, 366 p. (ISBN 978-0-387-96284-9).
↑ (en) Eberhard Knobloch, The intersection of history and mathematics, vol. 15, Basel, Boston, Berlin, Birkhäuser, 1994, « From Gauss to Weierstrass: determinant theory and its historical evaluations », p. 51–66
↑ (en) Thomas Hawkins, Cauchy and the spectral theory of matrices, vol. 2, Historia Mathematica, 1975, 1–29 p. (ISSN 0315-0860, DOI 10.1016/0315-0860(75)90032-4)
↑ (de) Kurt Hensel, Leopold Kronecker's Werke, Teubner, 1897 (lire en ligne)
↑ (de) Karl Weierstrass, Collected works, vol. 3, 1915 (lire en ligne), p. 271–286
↑ « Let us give the name of matrix to any function, of however many variables, which does not involve any apparent variables. Then any possible function other than a matrix is derived from a matrix by means of generalization, i.e., by considering the proposition which asserts that the function in question is true with all possible values or with some value of one of the arguments, the other argument or arguments remaining undetermined » . Alfred North Whitehead et Bertrand Russell, Principia Mathematica to *56, Cambridge at the University Press, Cambridge UK (1913, réédition de 1962) voir p. 162.
↑ (en) Alfred Tarski, Introduction to Logic and the Methodology of Deductive Sciences, Dover Publications, Inc, New York NY, 1946 (ISBN 0-486-28462-X). (lire en ligne)
↑ Voir N. Bourbaki, Algèbre, Chapitres 1 à 3, Springer, 2006, 2^e éd. (lire en ligne), A II.139, qui parle aussi de « matrice vide » dans le cas où $I$ ou $J$ est l'ensemble vide.
↑ On peut remarquer que ce produit est donné par une formule analogue à celle donnant le produit scalaire usuel ; cette remarque sera exploitée plus loin.
↑ Dans le cas plus général d'ensembles éventuellement infinis d'indices, on peut demander à $K$ d'être muni d'une topologie, pour définir le produit comme la somme d'une série (convergente). Sans topologie, on peut également demander aux colonnes (ou aux lignes) des matrices de ne contenir qu'un nombre fini d'éléments non nuls ; c'est d'ailleurs toujours le cas quand ces matrices représentent des applications linéaires entre espaces vectoriels munis de bases, même infinies. Paul Halmos, qui donne ces diverses définitions, ajoute néanmoins que « Not much of matrix theory carries over to infinite-dimensional spaces, and what does is not so useful, but it sometimes helps. » (la théorie des matrices s'étend peu aux espaces de dimension infinie, et ce qui s'étend n'est guère utile, mais peut parfois aider), dans P. Halmos, A Hilbert space problem book, 1982, p. 23.
1 2 Cette définition et les propriétés associées se généralisent à des $K$ -modules à droite libres de type fini sur un anneau (non nécessairement commutatif).
↑ Voir par exemple : (en) Henri Bourlès et Bogdan Marinescu, Linear Time-Varying Systems : Algebraic-Analytic Approach, Springer, 2011, 638 p. (ISBN 978-3-642-19726-0 et 3-642-19726-4, lire en ligne), §§ 2.2.4-2.2.6 ; cette formulation est très courante dans la théorie des D-modules.
↑ J. von Neumann (1937). Some matrix inequalities and metrization of matrix-space. Tomsk University Review, 1, 286–300. Collected Works, Pergamon, Oxford, 1962, Volume IV, 205-218

Voir aussi

Bibliographie

J.-M. Arnaudiès et H. Fraysse, Cours de mathématiques, Dunod, 1980
Rached Mneimné, Réduction des endomorphismes, Calvage et Mounet, Paris, 2006 (ISBN 978-2-916352-01-5)
P. Wira, Un rappel sur les matrices, support de cours, Université de Haute Alsace, Mulhouse, 2000

Liens externes

Frédéric Brechenmacher, Les matrices : formes de représentation et pratiques opératoires (1850-1930)