Loi de Henry

En physique, et plus particulièrement en thermodynamique, la loi de Henry, établie empiriquement par le physicien britannique William Henry en 1803^[1], énonce que^[2]^,^[3] :

« À température constante et à saturation, la pression partielle dans la phase vapeur d'un soluté volatil est proportionnelle à la fraction molaire de ce corps dans la solution liquide. »

En pratique, elle ne s'applique qu'aux faibles concentrations du soluté (fraction molaire inférieure à 0,05^[3]) et à des pressions de moins de 10 bar (domaine d'application de la loi des gaz parfaits). Le soluté peut être un gaz dissout ou plus généralement tout corps volatil très faiblement soluble ou très dilué. Elle n'est également appliquable qu'à des mélanges binaires, ne contenant qu'un seul soluté et un seul solvant. Par extension à l'aide de coefficients de fugacité et d'activité, elle peut être appliquée à des mélanges multicomposants réels. Le pendant de la loi de Henry pour les solvants est la loi de Raoult.

Elle est utilisée dans de nombreux domaines de la chimie, de la physique et de la météorologie.

Énoncé, définitions et démonstration

Énoncé de la loi de Henry

On considère une solution liquide constituée d'un soluté $\sigma$ dissout dans un solvant $s$ . La loi de Henry relie la pression partielle $P_{\sigma }$ du soluté en phase gazeuse à sa fraction molaire $x_{\sigma }^{\text{l}}$ en phase liquide à l'équilibre liquide-vapeur selon^[2]^,^[3] :

Loi de Henry
pression partielle du soluté

\sigma

dans le solvant

s

P_{\sigma }=x_{\sigma }^{\text{g}}P=x_{\sigma }^{\text{l}}k_{{\text{H}},\sigma ,s}

avec les notations :

$P$ la pression totale du mélange ;
$P_{\sigma }$ la pression partielle du soluté $\sigma$ , par définition $P_{\sigma }=x_{\sigma }^{\text{g}}P$ ;
$k_{{\text{H}},\sigma ,s}$ la constante de Henry du soluté $\sigma$ dans le solvant $s$ , aux pression $P$ et température $T$ du mélange ; la constante de Henry a la dimension d'une pression ; $k_{\text{H}}$ est la notation recommandée par le Green Book de l'Union internationale de chimie pure et appliquée (IUPAC)^[4], on trouve également $H$ , ${\mathcal {H}}$ voire $K$ dans la littérature ;
$x_{\sigma }^{\text{g}}$ la fraction molaire du soluté $\sigma$ dans la phase vapeur ;
$x_{\sigma }^{\text{l}}$ la fraction molaire du soluté $\sigma$ dans la phase liquide.

La littérature utilise parfois l'inverse de la constante de Henry $k_{\text{H}}$ définie précédemment, $H={1 \over k_{\text{H}}}$ , et l'appelle également constante de Henry. Sa dimension est alors l'inverse de celle d'une pression, et la loi de Henry énonce que^[5]^,^[6] :

« À température constante et à saturation, la quantité de gaz dissout dans un liquide est proportionnelle à la pression partielle qu'exerce ce gaz sur le liquide. »

et s'écrit sous la forme :

Loi de Henry :

x_{\sigma }^{\text{l}}=P_{\sigma }H_{\sigma ,s}

D'autres formes de la loi de Henry sont écrites en fonction de la concentration molaire ou de la molalité du soluté. Les lecteurs de littérature spécialisée doivent être attentifs à noter quelle version de l'équation de la loi de Henry est utilisée^[7] (voir le paragraphe Constantes de Henry pour des gaz dissouts dans l'eau).

La loi de Henry établissant l'état d'équilibre liquide-vapeur d'une solution liquide, les solutés considérés ici sont des espèces chimiques capables de passer en phase gaz dans les conditions de pression et de température considérées, c'est-à-dire des corps volatils, ce qui exclut les solutés solides tels les sels. Un soluté répondant à la loi de Henry est typiquement un corps gazeux dans les conditions de température et pression du mélange : soit un fluide supercritique (oxygène, azote pour un mélange dans les CNTP), soit un fluide subcritique ayant une pression de vapeur saturante supérieure à la pression du mélange (propane, butane pour un mélange dans les CNTP). Cependant, un soluté répondant à la loi de Henry peut être également un fluide subcritique liquide (ayant une pression de vapeur saturante inférieure à la pression du mélange, comme le pentane pour un mélange dans les CNTP) présent en faible quantité dans la solution, soit parce qu'il est fortement dilué, soit parce qu'il est peu soluble. De façon générale, un soluté $\sigma$ répondant à la loi de Henry est donc un corps volatil dans les conditions du mélange et dont la fraction molaire en phase liquide est faible, soit $x_{\sigma }^{\text{l}}\ll 1$ . Un solvant $s$ est un corps dont la fraction molaire en phase liquide est très supérieure à celle du soluté, soit $x_{s}^{\text{l}}\gg x_{\sigma }^{\text{l}}$ , se comportant quasiment comme un corps pur, soit $x_{s}^{\text{l}}\approx 1$ . La relation de Duhem-Margules impose que si l'équilibre liquide-vapeur d'un soluté répond à la loi de Henry, celui du solvant répond à la loi de Raoult.

L'équilibre liquide-vapeur déterminé par la loi de Henry est un état stable, appelé état de saturation du solvant par le soluté. Dans les conditions de pression et température données, le solvant peut contenir plus de soluté que la quantité déterminée par la loi de Henry, mais il s'agit alors d'un état d'équilibre instable dit de sursaturation. Dans ce cas la moindre perturbation (choc sur le récipient contenant le liquide, introduction d'une poussière formant un site de nucléation pour les bulles de gaz, fluctuation de pression ou de température, etc.) peut provoquer le dégazage de l'excès de soluté dissout jusqu'à l'établissement de l'état stable dicté par la loi. De même, la quantité du soluté dissout peut être inférieure à celle déterminée par la loi de Henry : il y a sous-saturation. Dans ce cas, si le soluté est présent en phase gaz, la phase liquide absorbe du soluté gazeux jusqu'à atteindre l'équilibre stable. La fraction $x_{\sigma }^{\text{l}}$ déterminée par la loi de Henry est donc la fraction molaire maximale de soluté que peut contenir la phase liquide de façon stable : la fraction $x_{\sigma }^{\text{l}}$ est la solubilité du soluté $\sigma$ dans le solvant $s$ dans les conditions de pression et de température données.

Constante de Henry

Les définitions et formules suivantes ne sont valables que pour un mélange binaire comprenant un unique soluté $\sigma$ et un unique solvant $s$ .

La constante de Henry est définie rigoureusement en thermodynamique à partir de la fugacité.

Contrairement à ce que peut laisser entendre le terme de constante, la constante de Henry dépend de la pression et de la température. En revanche, elle ne dépend pas de la composition du mélange. La constante de Henry $k_{{\text{H}},\sigma ,s}$ dépend également de la nature du soluté $\sigma$ et du solvant $s$ ; ceci implique qu'elle doit être déterminée pour chaque couple « soluté $\sigma$ - solvant $s$ » et n'est pas valable si l'un de ces deux corps est considéré dans un mélange binaire autre que celui pour lequel elle a été déterminée (par exemple le soluté $\sigma$ avec un solvant autre que le solvant $s$ ).

En pratique, la constante de Henry est déterminée expérimentalement.

Définition thermodynamique

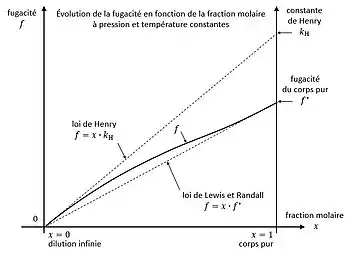
Évolution de la fugacité en fonction de la fraction molaire à pression et température constantes^[8]^,^[9].

En thermodynamique, à pression et température constantes, la fugacité $f_{\sigma }^{\text{l}}$ d'une espèce chimique $\sigma$ (soluté) en phase liquide, en présence d'une deuxième espèce $s$ (solvant), possède deux limites, avec $x_{\sigma }^{\text{l}}$ la fraction molaire du corps $\sigma$ dans le mélange :

à dilution infinie : $\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}f_{\sigma }^{\text{l}}=0$ ;
pour le corps pur : $\lim _{x_{\sigma }^{\text{l}}\to 1 \atop x_{s}^{\text{l}}\to 0}f_{\sigma }^{\text{l}}=f_{\sigma }^{{\text{l}},*}$ ;

avec $f_{\sigma }^{{\text{l}},*}$ la fugacité du corps $\sigma$ à l'état de liquide pur. Cette fugacité $f_{\sigma }^{{\text{l}},*}$ peut être fictive si le corps $\sigma$ est gazeux à l'état pur dans les conditions de pression et température données.

L'évolution de la fugacité en fonction de la composition est encadrée par deux lois linéaires^[8]^,^[9] :

Loi de Henry - aux faibles concentrations :

f_{\sigma }^{\text{l}}\approx x_{\sigma }^{\text{l}}k_{{\text{H}},\sigma ,s}

Loi de Lewis et Randall - aux fortes concentrations :

f_{\sigma }^{\text{l}}\approx x_{\sigma }^{\text{l}}f_{\sigma }^{{\text{l}},*}

La constante de Henry $k_{{\text{H}},\sigma ,s}$ n'est pas la fugacité du soluté $\sigma$ à dilution infinie dans le solvant $s$ . La fugacité $f_{\sigma }^{\text{l}}$ tend vers zéro lorsque $x_{\sigma }^{\text{l}}$ tend vers zéro. Aussi la constante de Henry est-elle définie comme étant la limite lorsque la quantité de soluté $\sigma$ dissout en phase liquide s'annule^[4]^,^[10]^,^[11]^,^[12] :

Constante de Henry :

k_{{\text{H}},\sigma ,s}=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}{f_{\sigma }^{\text{l}} \over x_{\sigma }^{\text{l}}}

à pression et température constantes.

avec :

$f_{\sigma }^{\text{l}}$ la fugacité du soluté $\sigma$ dans le mélange liquide ;
$k_{{\text{H}},\sigma ,s}$ la constante de Henry du soluté $\sigma$ dans le solvant $s$ , aux pression $P$ et température $T$ du mélange ;
$x_{\sigma }^{\text{l}}$ la fraction molaire du soluté $\sigma$ dans le mélange liquide ;
$x_{s}^{\text{l}}$ la fraction molaire du solvant $s$ dans le mélange liquide ( $x_{\sigma }^{\text{l}}+x_{s}^{\text{l}}=1$ ).

En application de la règle de L'Hôpital, la constante de Henry peut également être définie par^[4]^,^[11]^,^[12] :

Constante de Henry :

k_{{\text{H}},\sigma ,s}=\left({\partial f_{\sigma }^{\text{l}} \over \partial x_{\sigma }^{\text{l}}}\right)_{P,T,x_{\sigma }^{\text{l}}=0}

La constante de Henry est donc la pente de la fugacité à dilution infinie.

Quelle que soit la concentration $0\leq x_{\sigma }^{\text{l}}\leq 1$ du soluté $\sigma$ , sa fugacité réelle $f_{\sigma }^{\text{l}}$ peut être exprimée en fonction d'un coefficient d'activité à partir des deux lois linéaires idéales définies précédemment^[12]^,^[13] :

f_{\sigma }^{\text{l}}=x_{\sigma }^{\text{l}}\gamma _{{\text{H}},\sigma }^{\text{l}}k_{{\text{H}},\sigma ,s}=x_{\sigma }^{\text{l}}\gamma _{\sigma }^{\text{l}}f_{\sigma }^{{\text{l}},*}

en posant :

$\gamma _{{\text{H}},\sigma }^{\text{l}}$ le coefficient d'activité défini par rapport à la loi de Henry ;
$\gamma _{\sigma }^{\text{l}}$ le coefficient d'activité défini par rapport à la loi de Lewis et Randall.

Puisque les deux limites de la fugacité $f_{\sigma }^{\text{l}}$ sont définies, on a les limites des coefficients d'activité^[12]^,^[13] :

à dilution infinie : $\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\gamma _{{\text{H}},\sigma }^{\text{l}}=1$ ;
pour le corps pur : $\lim _{x_{\sigma }^{\text{l}}\to 1 \atop x_{s}^{\text{l}}\to 0}\gamma _{\sigma }^{\text{l}}=1$ .

On pose à dilution infinie^[12]^,^[13] :

Coefficient d'activité à dilution infinie :

\gamma _{\sigma ,s}^{{\text{l}},\infty }=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\gamma _{\sigma }^{\text{l}}

Par conséquent, à dilution infinie on a :

\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}{f_{\sigma }^{\text{l}} \over x_{\sigma }^{\text{l}}}=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\left(\gamma _{{\text{H}},\sigma }^{\text{l}}k_{{\text{H}},\sigma ,s}\right)=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\left(\gamma _{\sigma }^{\text{l}}f_{\sigma }^{{\text{l}},*}\right)

d'où la relation^[13]^,^[14] (puisque $k_{{\text{H}},\sigma ,s}$ et $f_{\sigma }^{{\text{l}},*}$ ne dépendent pas de la composition) :

Constante de Henry :

k_{{\text{H}},\sigma ,s}=\gamma _{\sigma ,s}^{{\text{l}},\infty }f_{\sigma }^{{\text{l}},*}

En injectant la relation précédente dans les expressions de $f_{\sigma }^{\text{l}}$ on obtient^[13]^,^[14] :

\gamma _{{\text{H}},\sigma }^{\text{l}}={\gamma _{\sigma }^{\text{l}} \over \gamma _{\sigma ,s}^{{\text{l}},\infty }}

La première relation permet de déterminer $k_{{\text{H}},\sigma ,s}$ si l'on connait $f_{\sigma }^{{\text{l}},*}$ . Inversement, connaissant $k_{{\text{H}},\sigma ,s}$ on peut extrapoler $f_{\sigma }^{{\text{l}},*}$ si le soluté $\sigma$ n'existe pas à l'état de liquide pur dans les conditions de pression et température données. La deuxième relation montre que les deux coefficients d'activité $\gamma _{{\text{H}},\sigma }^{\text{l}}$ et $\gamma _{\sigma }^{\text{l}}$ ne sont pas indépendants, bien que liés à des états de référence différents. La loi de Henry, quelle que soit sa forme, peut ainsi être employée avec les modèles classiques développés pour la loi de Lewis et Randall (Margules, Van Laar (en), Wilson^[13], NRTL (en), UNIQUAC, UNIFAC, COSMOSPACE, etc.).

Dépendance à la pression

La fugacité $f_{\sigma }^{\text{l}}$ du soluté $\sigma$ dans le mélange liquide varie en fonction de la pression selon :

\left({\partial \ln f_{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}={{\bar {V}}_{\sigma }^{\text{l}} \over RT}

avec :

$V^{\text{l}}$ le volume de la phase liquide ;
${\bar {V}}_{\sigma }^{\text{l}}=\left({\partial V^{\text{l}} \over \partial n_{\sigma }}\right)_{P,T,n_{s}}$ le volume molaire partiel du soluté $\sigma$ dans le mélange liquide ;
$n_{\sigma }$ la quantité du soluté $\sigma$ dans le mélange liquide ;
$n_{s}$ la quantité du solvant $s$ dans le mélange liquide.

Quelle que soit la fraction molaire $x_{\sigma }^{\text{l}}=n_{\sigma }/\left(n_{\sigma }+n_{s}\right)$ du soluté $\sigma$ , la dérivée partielle étant effectuée à composition constante, on peut écrire :

\left({\partial \ln f_{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}=\left({\partial \left[\ln f_{\sigma }^{\text{l}}-\ln x_{\sigma }^{\text{l}}+\ln x_{\sigma }^{\text{l}}\right] \over \partial P}\right)_{T,n}=\left({\partial \ln {f_{\sigma }^{\text{l}} \over x_{\sigma }^{\text{l}}} \over \partial P}\right)_{T,n}+\underbrace {\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}} _{=0\,{\text{à composition constante}}}

En passant à la limite de la dilution infinie :

\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\left({\partial \ln f_{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\left({\partial \ln {f_{\sigma }^{\text{l}} \over x_{\sigma }^{\text{l}}} \over \partial P}\right)_{T,n}=\left({\partial \ln k_{{\text{H}},\sigma ,s} \over \partial P}\right)_{T}

La référence à la composition constante disparait dans la dérivée partielle de la constante de Henry, puisque celle-ci ne dépend pas de la composition. On pose pour le volume molaire partiel^[15] :

Volume molaire partiel du soluté à dilution infinie :

{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}{\bar {V}}_{\sigma }^{\text{l}}

La constante de Henry dépend par conséquent de la pression selon^[15]^,^[16] :

Dépendance de la constante de Henry à la pression

\left({\partial \ln k_{{\text{H}},\sigma ,s} \over \partial P}\right)_{T}={{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty } \over RT}

avec :

$P$ la pression ;
$T$ la température ;
${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ le volume molaire partiel du soluté $\sigma$ à dilution infinie dans le solvant $s$ ;
$R$ la constante universelle des gaz parfaits.

En intégrant cette relation entre une pression de référence $P^{\circ }$ et la pression $P$ :

\ln k_{{\text{H}},\sigma ,s}\!\left(P,T\right)-\ln k_{{\text{H}},\sigma ,s}\!\left(P^{\circ },T\right)={\int _{P^{\circ }}^{P}{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\,\mathrm {d} P \over RT}

La pression de référence $P^{\circ }$ est le plus souvent prise égale à la pression de vapeur saturante du solvant $s$ à la température $T$ du mélange : $P^{\circ }=P_{s}^{\text{sat}}\!\left(T\right)$ . En conséquence, on peut réduire la constante d'intégration à une fonction de la température seule : $k_{{\text{H}},\sigma ,s}\!\left(P^{\circ },T\right)=k_{{\text{H}},\sigma ,s}^{\circ }\!\left(T\right)$ . La constante de Henry est alors exprimée sous la forme^[16]^,^[13]^,^[17] :

k_{{\text{H}},\sigma ,s}\!\left(P,T\right)=k_{{\text{H}},\sigma ,s}^{\circ }\!\left(T\right)\,{\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }

avec le facteur de Poynting^[13]^,^[17] :

Facteur de Poynting :

{\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }=\exp \!\left({\int _{P_{s}^{\text{sat}}}^{P}{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\,\mathrm {d} P \over RT}\right)

Le volume molaire partiel ${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ représente la variation de volume de la solution liquide due à la dissolution d'une mole de soluté $\sigma$ dans une quantité infinie de solvant $s$ . Il peut être déterminé expérimentalement par extrapolation de ${\bar {V}}_{\sigma }^{\text{l}}$ établi pour plusieurs concentrations de soluté dans le mélange liquide ; il existe également des corrélations telles que celle de Brelvi-O'Connell^[18]. Les liquides étant peu compressibles, le volume molaire partiel ${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ peut être considéré comme ne dépendant pas de la pression, soit ${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\approx {\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\!\left(T\right)$ , on obtient :

\ln k_{{\text{H}},\sigma ,s}\!\left(P,T\right)=\ln k_{{\text{H}},\sigma ,s}^{\circ }\!\left(T\right)+{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\cdot \left(P-P_{s}^{\text{sat}}\right) \over RT}

Il peut être aussi bien positif (la dissolution du gaz provoque une dilatation du liquide) que négatif (la dissolution du gaz provoque une contraction du liquide). Si le volume molaire partiel ${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ est positif alors la constante de Henry $k_{{\text{H}},\sigma ,s}$ augmente avec la pression $P$ .

Dépendance à la température

La fugacité $f_{\sigma }^{\text{l}}$ du soluté $\sigma$ dans le mélange liquide varie en fonction de la température selon :

\left({\partial \ln f_{\sigma }^{\text{l}} \over \partial {1 \over T}}\right)_{P,n}={{\bar {H}}_{\sigma }^{\text{l}}-{\bar {H}}_{\sigma }^{\bullet ,*} \over R}

avec :

$H^{\text{l}}$ l'enthalpie de la phase liquide ;
${\bar {H}}_{\sigma }^{\text{l}}=\left({\partial H^{\text{l}} \over \partial n_{\sigma }}\right)_{P,T,n_{s}}$ l'enthalpie molaire partielle du soluté $\sigma$ dans le mélange liquide ;
${\bar {H}}_{\sigma }^{\bullet ,*}$ l'enthalpie molaire du soluté $\sigma$ à l'état de gaz parfait pur à $T$ ;
$n_{\sigma }$ la quantité du soluté $\sigma$ dans le mélange liquide ;
$n_{s}$ la quantité du solvant $s$ dans le mélange liquide.

\left({\partial \ln f_{\sigma }^{\text{l}} \over \partial {1 \over T}}\right)_{P,n}=\left({\partial \left[\ln f_{\sigma }^{\text{l}}-\ln x_{\sigma }^{\text{l}}+\ln x_{\sigma }^{\text{l}}\right] \over \partial {1 \over T}}\right)_{P,n}=\left({\partial \ln {f_{\sigma }^{\text{l}} \over x_{\sigma }^{\text{l}}} \over \partial {1 \over T}}\right)_{P,n}+\underbrace {\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial {1 \over T}}\right)_{P,n}} _{=0\,{\text{à composition constante}}}

En passant à la limite de la dilution infinie :

\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\left({\partial \ln f_{\sigma }^{\text{l}} \over \partial {1 \over T}}\right)_{P,n}=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\left({\partial \ln {f_{\sigma }^{\text{l}} \over x_{\sigma }^{\text{l}}} \over \partial {1 \over T}}\right)_{P,n}=\left({\partial \ln k_{{\text{H}},\sigma ,s} \over \partial {1 \over T}}\right)_{P}

La référence à la composition constante disparait dans la dérivée partielle de la constante de Henry, puisque celle-ci ne dépend pas de la composition. On pose pour l'enthalpie molaire partielle^[15]^,^[19] :

Enthalpie molaire partielle à dilution infinie du soluté $\sigma$ :

{\bar {H}}_{\sigma ,s}^{{\text{l}},\infty }=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}{\bar {H}}_{\sigma }^{\text{l}}

c'est-à-dire l'enthalpie molaire partielle du soluté $\sigma$ à dilution infinie dans le solvant $s$ liquide. L'enthalpie molaire du gaz parfait pur ${\bar {H}}_{\sigma }^{\bullet ,*}$ ne dépendant pas de la composition, elle reste inchangée lors du passage à la limite et on obtient :

\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\left({\bar {H}}_{\sigma }^{\text{l}}-{\bar {H}}_{\sigma }^{\bullet ,*}\right)={\bar {H}}_{\sigma ,s}^{{\text{l}},\infty }-{\bar {H}}_{\sigma }^{\bullet ,*}

On pose pour les enthalpies molaires partielles^[15]^,^[19] :

Enthalpie de dissolution :

\Delta _{\text{sol}}H_{\sigma ,s}={\bar {H}}_{\sigma ,s}^{{\text{l}},\infty }-{\bar {H}}_{\sigma }^{\bullet ,*}

avec :

${\bar {H}}_{\sigma ,s}^{{\text{l}},\infty }$ l'enthalpie molaire partielle du soluté $\sigma$ à dilution infinie dans le solvant $s$ liquide à $T$ ;
${\bar {H}}_{\sigma }^{\bullet ,*}$ l'enthalpie molaire du soluté $\sigma$ à l'état de gaz parfait pur à $T$ .

La constante de Henry dépend par conséquent de la température selon^[15]^,^[19] :

Dépendance de la constante de Henry à la température

\left({\partial \ln k_{{\text{H}},\sigma ,s} \over \partial {1 \over T}}\right)_{P}={\Delta _{\text{sol}}H_{\sigma ,s} \over R}

avec :

$P$ la pression ;
$T$ la température ;
$\Delta _{\text{sol}}H_{\sigma ,s}$ l'enthalpie de dissolution^[20] du soluté $\sigma$ dans le solvant $s$ à $T$ ;
$R$ la constante universelle des gaz parfaits.

Si l'on considère l'enthalpie de dissolution $\Delta _{\text{sol}}H_{\sigma ,s}$ comme constante, alors, en intégrant cette relation entre une température de référence $T^{\circ }$ et la température $T$ ^[19] :

\ln k_{{\text{H}},\sigma ,s}\!\left(P,T\right)-\ln k_{{\text{H}},\sigma ,s}\!\left(P,T^{\circ }\right)={\Delta _{\text{sol}}H_{\sigma ,s} \over R}\left({1 \over T}-{1 \over T^{\circ }}\right)

k_{{\text{H}},\sigma ,s}\!\left(P,T\right)=k_{{\text{H}},\sigma ,s}\!\left(P,T^{\circ }\right)\cdot \exp \!\left({\Delta _{\text{sol}}H_{\sigma ,s} \over R}\left({1 \over T}-{1 \over T^{\circ }}\right)\right)

Cette forme n'est applicable que sur des plages de température relativement étroites. Elle est généralisée au moyen de deux constantes $A$ et $B$ empiriques spécifiques du couple « soluté $\sigma$ - solvant $s$ »^[21] :

\ln k_{{\text{H}},\sigma ,s}\!\left(P,T\right)=A+{B \over T}

La littérature utilise parfois l'inverse de la constante de Henry définie précédemment, $H_{\sigma ,s}={1 \over k_{{\text{H}},\sigma ,s}}$ (cette notation prête à confusion avec celle de l'enthalpie de dissolution $\Delta _{\text{sol}}H_{\sigma ,s}$ ^[7]), aussi trouve-t-on également les relations^[7] :

\left({\partial \ln H_{\sigma ,s} \over \partial {1 \over T}}\right)_{P}=-{\Delta _{\text{sol}}H_{\sigma ,s} \over R}

\ln H_{\sigma ,s}\!\left(P,T\right)-\ln H_{\sigma ,s}\!\left(P,T^{\circ }\right)=-{\Delta _{\text{sol}}H_{\sigma ,s} \over R}\left({1 \over T}-{1 \over T^{\circ }}\right)

H_{\sigma ,s}\!\left(P,T\right)=H_{\sigma ,s}\!\left(P,T^{\circ }\right)\cdot \exp \!\left(-{\Delta _{\text{sol}}H_{\sigma ,s} \over R}\left({1 \over T}-{1 \over T^{\circ }}\right)\right)

L'enthalpie de dissolution $\Delta _{\text{sol}}H_{\sigma ,s}$ est la chaleur produite par la dissolution d'une mole de soluté $\sigma$ à l'état de gaz parfait pur dans une quantité infinie de solvant $s$ à l'état liquide^[19]. Elle est déterminée expérimentalement par calorimétrie en extrapolant la chaleur de dissolution d'une mole de soluté dans plusieurs quantités de solvant. On peut considérer l'enthalpie molaire partielle d'un corps dans un mélange liquide, ici ${\bar {H}}_{\sigma ,s}^{{\text{l}},\infty }$ , comme indépendante de la pression, les liquides étant peu compressibles. De même, en vertu de la deuxième loi de Joule, l'enthalpie molaire d'un gaz parfait, ici ${\bar {H}}_{\sigma }^{\bullet ,*}$ , ne dépend pas de la pression. Ainsi, il peut être considéré que l'enthalpie de dissolution ne dépend que de la température : $\Delta _{\text{sol}}H_{\sigma ,s}=\Delta _{\text{sol}}H_{\sigma ,s}\!\left(T\right)$ . Elle peut être négative (dissolution exothermique, l'opération de dissolution dégage de la chaleur), positive (dissolution endothermique, l'opération de dissolution absorbe de la chaleur) ou nulle (dissolution athermique)^[19]. Pour la plupart des gaz à température ambiante la dissolution est exothermique, soit $\Delta _{\text{sol}}H_{\sigma ,s}<0$ , par conséquent $\ln k_{{\text{H}},\sigma ,s}$ augmente avec une diminution de ${1 \over T}$ et la constante de Henry $k_{{\text{H}},\sigma ,s}$ augmente avec la température $T$ .

Calcul théorique par une équation d'état

Le coefficient de fugacité $\phi _{\sigma }^{\text{l}}$ du soluté $\sigma$ en phase liquide est défini par la relation avec la fugacité $f_{\sigma }^{\text{l}}$ :

Coefficient de fugacité :

\phi _{\sigma }^{\text{l}}={f_{\sigma }^{\text{l}} \over x_{\sigma }^{\text{l}}P}

Par définition de la constante de Henry, on a donc^[14]^,^[22] :

k_{{\text{H}},\sigma ,s}=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\left(\phi _{\sigma }^{\text{l}}P\right)

à pression et température constantes

Si l'on dispose d'une équation d'état d'une phase liquide donnant la pression $P$ en fonction du volume $V^{\text{l}}$ , de la température $T$ et de la composition $n$ , soit $P=P\!\left(V^{\text{l}},T,n\right)$ , le coefficient de fugacité $\phi _{\sigma }^{\text{l}}$ se calcule selon :

RT\,\ln \phi _{\sigma }^{\text{l}}=-\int _{+\infty }^{V^{\text{l}}}\left[\left({\partial P \over \partial n_{\sigma }}\right)_{V,T,n_{s}}-{RT \over V}\right]\,\mathrm {d} V-RT\,\ln \!\left({PV^{\text{l}} \over \left(n_{\sigma }+n_{s}\right)RT}\right)

avec $n_{\sigma }$ la quantité du soluté $\sigma$ et $n_{s}$ la quantité du solvant $s$ . Il est donc possible de calculer la constante de Henry $k_{{\text{H}},\sigma ,s}$ à partir d'une équation d'état de la phase liquide. Toutefois, les équations d'état telles que les équations d'état cubiques sont généralement développées pour représenter des phases gazeuses et représentent assez mal les phases liquides. Cette démarche reste donc théorique ; en pratique la constante de Henry est plutôt déterminée expérimentalement sous des formes empiriques présentées au paragraphe Formes usuelles. La relation établie ci-dessus et l'exemple ci-dessous montrent cependant la dépendance de la constante de Henry $k_{{\text{H}},\sigma ,s}$ aux propriétés du solvant $s$ et du soluté $\sigma$ , et aux interactions entre les deux constituants.

Exemple - Avec l'équation d'état de van der Waals^[22].

L'équation d'état de van der Waals donne :

P={RT \over {\bar {V}}^{\text{l}}-b_{m}}-{a_{m} \over {{\bar {V}}^{\text{l}}}^{2}}

RT\ln \phi _{\sigma }^{\text{l}}=-{a_{m} \over {\bar {V}}^{\text{l}}}\left[\delta _{\sigma }-{b_{\sigma } \over b_{m}}\right]+{b_{\sigma } \over b_{m}}\left(P{\bar {V}}^{\text{l}}-RT\right)-RT\,\ln \!\left({P\!\cdot \!\left({\bar {V}}^{\text{l}}-b_{m}\right) \over RT}\right)

avec :

a_{m}={x_{\sigma }^{\text{l}}}^{2}a_{\sigma }+2\,x_{\sigma }^{\text{l}}x_{s}^{\text{l}}{\sqrt {a_{\sigma }a_{s}}}\left(1-k_{\sigma ,s}\right)+{x_{s}^{\text{l}}}^{2}a_{s}

b_{m}=x_{\sigma }^{\text{l}}b_{\sigma }+x_{s}^{\text{l}}b_{s}

\delta _{\sigma }=2{{\sqrt {a_{\sigma }}} \over a_{m}}\left(x_{\sigma }^{\text{l}}{\sqrt {a_{\sigma }}}+x_{s}^{\text{l}}{\sqrt {a_{s}}}\left(1-k_{\sigma ,s}\right)\right)

À dilution infinie ( $x_{\sigma }^{\text{l}}\to 0$ et $x_{s}^{\text{l}}\to 1$ ) on a :

a_{m}\to a_{s}

b_{m}\to b_{s}

\delta _{\sigma }\to \delta _{\sigma }^{\infty }=2\,{\sqrt {a_{\sigma } \over a_{s}}}\left(1-k_{\sigma ,s}\right)

Le volume molaire ${\bar {V}}^{\text{l}}$ de la solution liquide tend vers celui ${\bar {V}}_{s}^{\text{l,*}}$ du solvant $s$ liquide pur, calculable par l'équation d'état : ${\bar {V}}^{\text{l}}\to {\bar {V}}_{s}^{\text{l,*}}$ . On obtient, à pression et température constantes :

\ln k_{{\text{H}},\sigma ,s}\!\left(P,T\right)=-{a_{s} \over RT\,{\bar {V}}_{s}^{\text{l,*}}}\left[\delta _{\sigma }^{\infty }-{b_{\sigma } \over b_{s}}\right]+{b_{\sigma } \over b_{s}}\left({P{\bar {V}}_{s}^{\text{l,*}} \over RT}-1\right)-\ln \!\left({{\bar {V}}_{s}^{\text{l,*}}-b_{s} \over RT}\right)

Lorsque la pression $P$ tend vers la pression de vapeur saturante $P_{s}^{\text{sat}}$ du solvant $s$ à la température $T$ , l'équilibre liquide-vapeur tend vers celui du solvant $s$ pur (état de saturation) ; le volume molaire ${\bar {V}}_{s}^{\text{l,*}}$ tend vers celui ${\bar {V}}_{s}^{\text{l,*,sat}}$ du solvant $s$ liquide pur à saturation. On peut donc calculer la constante de Henry dans les conditions de saturation du solvant $s$ ^[22] :

\ln k_{{\text{H}},\sigma ,s}\!\left(P_{s}^{\text{sat}},T\right)=-{a_{s} \over RT\,{\bar {V}}_{s}^{\text{l,*,sat}}}\left[\delta _{\sigma }^{\infty }-{b_{\sigma } \over b_{s}}\right]+{b_{\sigma } \over b_{s}}\left({P_{s}^{\text{sat}}{\bar {V}}_{s}^{\text{l,*,sat}} \over RT}-1\right)-\ln \!\left({{\bar {V}}_{s}^{\text{l,*,sat}}-b_{s} \over RT}\right)

Les liquides étant peu compressibles, le volume molaire ${\bar {V}}_{s}^{\text{l,*}}$ du solvant $s$ liquide pur est assimilable à celui ${\bar {V}}_{s}^{\text{l,*,sat}}$ du solvant $s$ liquide pur à saturation : ${\bar {V}}_{s}^{\text{l,*}}\approx {\bar {V}}_{s}^{\text{l,*,sat}}$ . On peut alors calculer avec le facteur de Poynting :

\ln k_{{\text{H}},\sigma ,s}\!\left(P,T\right)\approx \ln k_{{\text{H}},\sigma ,s}\!\left(P_{s}^{\text{sat}},T\right)+{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\cdot \left(P-P_{s}^{\text{sat}}\right) \over RT}

d'où le volume molaire partiel du soluté $\sigma$ à dilution infinie dans le solvant $s$ :

{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\approx {b_{\sigma } \over b_{s}}{\bar {V}}_{s}^{\text{l,*,sat}}

Avec :

$a_{\sigma }={27R^{2}{T_{{\text{c}},\sigma }}^{2} \over 64P_{{\text{c}},\sigma }}$ et $a_{s}={27R^{2}{T_{{\text{c}},s}}^{2} \over 64P_{{\text{c}},s}}$ ;
$b_{\sigma }={R{T_{{\text{c}},\sigma }} \over 8P_{{\text{c}},\sigma }}$ et $b_{s}={R{T_{{\text{c}},s}} \over 8P_{{\text{c}},s}}$ ;
$k_{\sigma ,s}$ un coefficient d'interaction binaire ;
$P_{{\text{c}},\sigma }$ et $P_{{\text{c}},s}$ les pressions critiques respectives du soluté $\sigma$ et du solvant $s$ ;
$P_{s}^{\text{sat}}$ la pression de vapeur saturante du solvant $s$ à la température $T$ ;
$T_{{\text{c}},\sigma }$ et $T_{{\text{c}},s}$ les températures critiques respectives du soluté $\sigma$ et du solvant $s$ ;
${\bar {V}}^{\text{l}}$ le volume molaire de la solution liquide à la pression $P$ et à la température $T$ ;
${\bar {V}}_{s}^{\text{l,*}}$ le volume molaire du solvant $s$ liquide pur à $P$ et $T$ ;
${\bar {V}}_{s}^{\text{l,*,sat}}$ le volume molaire du solvant $s$ liquide pur à saturation, soit à $P_{s}^{\text{sat}}$ et $T$ .

Cet exemple montre la dépendance de la constante de Henry $k_{{\text{H}},\sigma ,s}$ aux propriétés du solvant $s$ et du soluté $\sigma$ , et aux interactions entre le soluté $\sigma$ et le solvant $s$ par l'intermédiaire du coefficient d'interaction binaire $k_{\sigma ,s}$ ^[22]. La constante de Henry est donc spécifique du couple « soluté $\sigma$ - solvant $s$ » et ne peut être utilisée pour d'autres mélanges binaires ; par exemple, elle n'est pas valable si le soluté $\sigma$ est dissout dans un solvant autre que $s$ .

Formes usuelles

La constante de Henry est souvent utilisée sous la forme obtenue par intégration par rapport à la pression^[17] :

Forme usuelle de la constante de Henry

k_{{\text{H}},\sigma ,s}\!\left(P,T\right)=k_{{\text{H}},\sigma ,s}^{\circ }\!\left(T\right)\cdot \exp \!\left({{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\cdot \left(P-P_{s}^{\text{sat}}\right) \over RT}\right)

La correction de Poynting ne devient significative qu'aux hautes pressions. Pour des pressions de l'ordre de grandeur de la pression atmosphérique, le facteur de Poynting est négligeable : ${\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }\approx 1$ . La constante de Henry peut alors être considérée comme indépendante de la pression et être approchée par :

Aux basses pressions :

k_{{\text{H}},\sigma ,s}\!\left(P,T\right)\approx k_{{\text{H}},\sigma ,s}^{\circ }\!\left(T\right)

Les formes suivantes sont souvent utilisées pour la dépendance à la température^[21]^,^[23] :

\ln k_{{\text{H}},\sigma ,s}^{\circ }\!\left(T\right)=A+{B \over T}+C\,\ln T+D\,T

\ln k_{{\text{H}},\sigma ,s}^{\circ }\!\left(T\right)=A+{B \over T}+{C \over T^{2}}+{D \over T^{3}}

avec $A$ , $B$ , $C$ et $D$ des constantes empiriques spécifiques du couple « soluté $\sigma$ - solvant $s$ ». L'enthalpie de dissolution est alors exprimée sous les formes respectives :

{\Delta _{\text{sol}}H_{\sigma ,s} \over R}=B-C\,T-D\,T^{2}

{\Delta _{\text{sol}}H_{\sigma ,s} \over R}=B+{2\,C \over T}+{3\,D \over T^{2}}

Démonstration de la loi de Henry

Lorsque l'équilibre liquide-vapeur est atteint, les fugacités du soluté $\sigma$ sont homogènes entre les deux phases^[24] :

f_{\sigma }^{\text{g}}=f_{\sigma }^{\text{l}}

avec :

$f_{\sigma }^{\text{g}}$ la fugacité du soluté $\sigma$ en phase gaz (vapeur) ;
$f_{\sigma }^{\text{l}}$ la fugacité du soluté $\sigma$ en phase liquide.

Aux basses pressions (moins de 10 bar), le gaz se comporte comme un mélange de gaz parfaits, et la fugacité du soluté $\sigma$ en phase gaz peut être assimilée à sa pression partielle^[25] :

f_{\sigma }^{\text{g}}\approx x_{\sigma }^{\text{g}}P

D'autre part, par définition, aux faibles concentrations la fugacité du soluté $\sigma$ dans le solvant $s$ en phase liquide suit approximativement la loi linéaire^[25] :

f_{\sigma }^{\text{l}}\approx x_{\sigma }^{\text{l}}k_{{\text{H}},\sigma ,s}

Ainsi, aux basses pressions et aux faibles concentrations, l'équilibre liquide-vapeur du soluté $\sigma$ est approché par la relation :

x_{\sigma }^{\text{g}}P=x_{\sigma }^{\text{l}}k_{{\text{H}},\sigma ,s}

qui est la loi de Henry^[25]. Aux fortes concentrations, la fugacité en phase liquide suit approximativement la loi de Lewis et Randall : aux basses pressions et aux fortes concentrations ceci conduit à la loi de Raoult qui s'applique aux solvants.

Limites et extensions de la loi de Henry

Limites de la loi idéale

Conditions de pression

La loi de Henry n'est valable que si la phase gaz peut être considérée comme un mélange de gaz parfaits. Autrement dit, elle ne s'applique qu'à des pressions partielles de soluté de l'ordre de la pression atmosphérique (moins de 10 bar), dans le domaine d'application de la loi des gaz parfaits^[26].

Composition de la phase liquide

Concentration du soluté

La loi de Henry est une loi limitante qui ne s'applique qu'aux solutions suffisamment diluées. La gamme de concentrations à laquelle elle s'applique se restreint à mesure que le système diverge par rapport au comportement idéal ; pour faire simple, cela signifie à mesure que le soluté a un comportement chimiquement différent du solvant. Typiquement, la loi de Henry s'applique uniquement si la fraction molaire $x_{\sigma }^{\text{l}}$ du soluté est inférieure à 0,03^[26] ou 0,05^[3].

Présence d'autres solutés

La loi de Henry est établie pour un soluté unique dissout dans un solvant unique. Si le solvant contient plusieurs solutés la constante de Henry est modifiée et dépend de la composition. Ainsi la solubilité d'un gaz dans l'eau de mer est-elle inférieure à celle dans l'eau douce en raison de la compétition entre le gaz dissout et les sels dissouts. La constante de Henry pourra être corrigée selon l'équation empirique de Setchenov^[7]^,^[27]^,^[23] :

Équation de Setchenov :

\ln {k_{{\text{H}},\sigma ,s} \over k_{{\text{H}},\sigma ,s}^{*}}=kI

avec :

$k_{{\text{H}},\sigma ,s}$ la constante de Henry du soluté $\sigma$ dans le solvant $s$ en solution avec tous les solutés ;
$k_{{\text{H}},\sigma ,s}^{*}$ la constante de Henry du soluté $\sigma$ dans le solvant $s$ en solution avec $\sigma$ seul soluté ;
$k$ le coefficient de Setchenov, qui dépend des solutés et du solvant ;
$I$ la force ionique ; on trouve aussi cette équation exprimée en fonction de la molalité des sels dissouts^[7].

Dissolution réactive

La loi de Henry s'applique uniquement aux solutions dans lesquelles le soluté ne réagit pas chimiquement avec le solvant. Un exemple usuel dans lequel le gaz réagit avec le solvant est le dioxyde de carbone (CO₂), qui forme partiellement, par réaction avec l'eau, de l'acide carbonique (H₂CO₃), qui lui-même, en fonction du pH de l'eau, forme les ions hydrogénocarbonate (HCO₃⁻) et carbonate (CO₃²⁻). En conséquence, plus le pH de l'eau est basique, plus l'on peut dissoudre de dioxyde de carbone dans l'eau.

Cas des solvants, loi de Raoult

Un solvant $s$ est un corps présent dans une solution liquide ayant une fraction molaire très supérieure à celle d'un soluté $\sigma$ , soit $x_{s}^{\text{l}}\gg x_{\sigma }^{\text{l}}$ . Ce corps peut quasiment être considéré comme pur, soit $x_{s}^{\text{l}}\approx 1$ .

La relation de Duhem-Margules implique que si un soluté suit la loi de Henry, alors le solvant suit la loi de Raoult qui relie sa pression partielle $P_{s}$ en phase gazeuse à sa fraction molaire $x_{s}^{\text{l}}$ en phase liquide à l'équilibre liquide-vapeur selon :

Loi de Raoult :

P_{s}=x_{s}^{\text{g}}P=x_{s}^{\text{l}}P_{s}^{\text{sat}}{\mathcal {P}}_{s}^{{\text{l}},*}

avec :

$P$ la pression totale du mélange ;
$P_{s}$ la pression partielle du solvant $s$ , par définition $P_{s}=x_{s}^{\text{g}}P$ ;
$P_{s}^{\text{sat}}$ la pression de vapeur saturante du composé $s$ à la température $T$ du mélange ;
${\mathcal {P}}_{s}^{{\text{l}},*}=\exp \!\left({\int _{P_{s}^{\text{sat}}}^{P}{\bar {V}}_{s}^{{\text{l}},*}\,\mathrm {d} P \over RT}\right)$ le facteur de Poynting appliqué au solvant $s$ ;
${\bar {V}}_{s}^{{\text{l}},*}$ le volume molaire du solvant $s$ liquide pur ;
$x_{s}^{\text{g}}$ la fraction molaire du solvant $s$ dans la phase vapeur ;
$x_{s}^{\text{l}}$ la fraction molaire du solvant $s$ dans la phase liquide.

La relation de Duhem-Margules induit également que si l'on néglige la correction de Poynting pour le soluté, alors elle est également négligeable pour le solvant, soit ${\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }={\mathcal {P}}_{s}^{{\text{l}},*}=1$ .

Extensions aux mélanges réels

La loi de Henry constitue une base pour calculer les équilibres liquide-vapeur des mélanges réels, non idéaux, entre autres à des concentrations et des pressions plus fortes que celles données précédemment. À l'équilibre liquide-vapeur, on a pour tout corps $i$ , soluté ou solvant, l'égalité des fugacités en phase vapeur et en phase liquide, soit :

f_{i}^{\text{g}}=f_{i}^{\text{l}}

La fugacité réelle en phase gaz $f_{i}^{\text{g}}$ s'écrit à l'aide d'un coefficient de fugacité $\phi _{i}^{\text{g}}$ corrigeant la loi des gaz parfaits. La fugacité réelle en phase liquide $f_{i}^{\text{l}}$ s'écrit à partir de la fugacité à l'état de corps pur $f_{i}^{\text{l,*}}$ à l'aide d'un coefficient d'activité $\gamma _{i}^{\text{l}}$ corrigeant la loi de Lewis et Randall :

f_{i}^{\text{g}}=x_{i}^{\text{g}}\phi _{i}^{\text{g}}P

f_{i}^{\text{l}}=x_{i}^{\text{l}}\gamma _{i}^{\text{l}}f_{i}^{\text{l,*}}

Mélanges binaires

On considère un mélange binaire ne comprenant qu'un unique soluté $\sigma$ et un unique solvant $s$ .

Lois des équilibres binaires

La fugacité (fictive si le soluté est un gaz) $f_{\sigma }^{\text{l,*}}$ du soluté $\sigma$ à l'état de liquide pur est donnée par la relation^[13] :

f_{\sigma }^{\text{l,*}}={k_{{\text{H}},\sigma ,s} \over \gamma _{\sigma ,s}^{{\text{l}},\infty }}={k_{{\text{H}},\sigma ,s}^{\circ } \over \gamma _{\sigma ,s}^{{\text{l}},\infty }}{\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }

Pour le soluté $\sigma$ , l'équilibre liquide-vapeur est calculé par l'extension de la loi de Henry^[17] :

Extension de la loi de Henry aux mélanges binaires réels
pour le soluté

\sigma

x_{\sigma }^{\text{g}}\phi _{\sigma }^{\text{g}}P=x_{\sigma }^{\text{l}}{\gamma _{\sigma }^{\text{l}} \over \gamma _{\sigma ,s}^{{\text{l}},\infty }}k_{{\text{H}},\sigma ,s}^{\circ }{\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }

Pour le solvant $s$ , l'équilibre liquide-vapeur est calculé par l'extension de la loi de Raoult^[17] :

Extension de la loi de Raoult aux mélanges binaires réels
pour le solvant

s

x_{s}^{\text{g}}\phi _{s}^{\text{g}}P=x_{s}^{\text{l}}\gamma _{s}^{\text{l}}\phi _{s}^{\text{g,*,sat}}P_{s}^{\text{sat}}{\mathcal {P}}_{s}^{{\text{l}},*}

avec $f_{s}^{\text{l,*}}=\phi _{s}^{\text{g,*,sat}}P_{s}^{\text{sat}}{\mathcal {P}}_{s}^{{\text{l}},*}$ la fugacité du solvant $s$ liquide pur dans les conditions de pression et température du mélange.

En application du théorème d'Euler, le volume molaire ${\bar {V}}^{\text{l}}$ de la phase liquide vaut :

{\begin{aligned}{{\bar {V}}^{\text{l}} \over RT}&={x_{\sigma }^{\text{l}}{\bar {V}}_{\sigma }^{\text{l}}+x_{s}^{\text{l}}{\bar {V}}_{s}^{\text{l}} \over RT}=x_{\sigma }^{\text{l}}\left({\partial \ln f_{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}+x_{s}^{\text{l}}\left({\partial \ln f_{s}^{\text{l}} \over \partial P}\right)_{T,n}\\&=x_{\sigma }^{\text{l}}\left[{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty } \over RT}-\left({\partial \ln \gamma _{\sigma ,s}^{{\text{l}},\infty } \over \partial P}\right)_{T,n}+\left({\partial \ln \gamma _{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}\right]+x_{s}^{\text{l}}\left[{{\bar {V}}_{s}^{{\text{l}},*} \over RT}+\left({\partial \ln \gamma _{s}^{\text{l}} \over \partial P}\right)_{T,n}\right]\end{aligned}}

Le plus souvent, les modèles d'activité $\gamma _{i}^{\text{l}}$ ne dépendent pas de la pression, le volume molaire est alors calculé selon le modèle idéal.

Lois des équilibres binaires idéaux

Si le mélange liquide est idéal, alors $\gamma _{\sigma ,s}^{{\text{l}},\infty }=\gamma _{\sigma }^{\text{l}}=\gamma _{s}^{\text{l}}=1$ . Pour des pressions proches de la pression atmosphérique (moins de 10 bar) le gaz se comporte comme un gaz parfait, soit $\phi _{\sigma }^{\text{g}}=\phi _{s}^{\text{g}}=\phi _{s}^{\text{g,*,sat}}=1$ . Pour un mélange liquide binaire idéal aux basses pressions on retrouve par conséquent les lois idéales :

Loi de Henry pour le soluté

\sigma

x_{\sigma }^{\text{g}}P=x_{\sigma }^{\text{l}}k_{{\text{H}},\sigma ,s}^{\circ }{\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }

et :

Loi de Raoult pour le solvant

s

x_{s}^{\text{g}}P=x_{s}^{\text{l}}P_{s}^{\text{sat}}{\mathcal {P}}_{s}^{{\text{l}},*}

Le volume molaire ${\bar {V}}^{\text{l,id}}$ de la phase liquide idéale vaut :

{\bar {V}}^{\text{l,id}}=x_{\sigma }^{\text{l}}{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }+x_{s}^{\text{l}}{\bar {V}}_{s}^{{\text{l}},*}

Équations de Krichevsky-Kasarnovsky et Krichevsky-Ilinskaya

En supposant que le volume molaire ${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ ne dépend pas de la pression, on développe le facteur de Poynting ${\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }$ . On obtient, pour tout soluté $\sigma$ :

\ln {f_{\sigma }^{\text{g}} \over x_{\sigma }^{\text{l}}}=\ln \!\left({\gamma _{\sigma }^{\text{l}} \over \gamma _{\sigma ,s}^{{\text{l}},\infty }}k_{{\text{H}},\sigma ,s}^{\circ }{\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }\right)=\ln k_{{\text{H}},\sigma ,s}^{\circ }+\ln \gamma _{\sigma }^{\text{l}}-\ln \gamma _{\sigma ,s}^{{\text{l}},\infty }+{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\cdot \left(P-P_{s}^{\text{sat}}\right) \over RT}

Si le coefficient d'activité suit le modèle de Margules à un paramètre :

\ln \gamma _{\sigma }^{\text{l}}=A\,{x_{s}^{\text{l}}}^{2}

\ln \gamma _{\sigma ,s}^{{\text{l}},\infty }=\lim _{x_{\sigma }^{\text{l}}\to 0 \atop x_{s}^{\text{l}}\to 1}\ln \gamma _{\sigma }^{\text{l}}=A

avec $x_{s}^{\text{l}}$ la fraction molaire du solvant $s$ dans la phase liquide (avec $x_{s}^{\text{l}}+x_{\sigma }^{\text{l}}=1$ ). On obtient l'équation de Krichevsky-Ilinskaya^[28]^,^[29] :

Équation de Krichevsky-Ilinskaya

\ln {f_{\sigma }^{\text{g}} \over x_{\sigma }^{\text{l}}}=\ln k_{{\text{H}},\sigma ,s}^{\circ }+A\cdot \left({x_{s}^{\text{l}}}^{2}-1\right)+{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\cdot \left(P-P_{s}^{\text{sat}}\right) \over RT}

que l'on trouve aussi, en écrivant le modèle de coefficient d'activité selon $RT\,\ln \gamma _{\sigma }^{\text{l}}=A\,{x_{s}^{\text{l}}}^{2}$ , sous la forme^[30]^,^[31]^,^[32]^,^[23] :

Équation de Krichevsky-Ilinskaya

\ln {f_{\sigma }^{\text{g}} \over x_{\sigma }^{\text{l}}}=\ln k_{{\text{H}},\sigma ,s}^{\circ }+{A \over RT}\cdot \left({x_{s}^{\text{l}}}^{2}-1\right)+{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\cdot \left(P-P_{s}^{\text{sat}}\right) \over RT}

Si le mélange liquide est idéal, soit $\gamma _{\sigma }^{\text{l}}=\gamma _{\sigma ,s}^{{\text{l}},\infty }=1$ (d'où $A=0$ ), on obtient l'équation de Krichevsky–Kasarnovsky^[16]^,^[29]^,^[33]^,^[34]^,^[23] :

Équation de Krichevsky–Kasarnovsky

\ln {f_{\sigma }^{\text{g}} \over x_{\sigma }^{\text{l}}}=\ln k_{{\text{H}},\sigma ,s}^{\circ }+{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }\cdot \left(P-P_{s}^{\text{sat}}\right) \over RT}

L'équation de Krichevsky-Kasarnovsky ne s'emploie que pour de faibles concentrations de soluté (solutions liquides idéales), l'équation de Krichevsky-Ilinskaya est valable pour des concentrations plus fortes. Pour des pressions proches de la pression atmosphérique (moins de 10 bar) le gaz se comporte comme un gaz parfait, la fugacité du soluté $\sigma$ en phase vapeur est alors égale à sa pression partielle : $f_{\sigma }^{\text{g}}=x_{\sigma }^{\text{g}}P$ . Pour des pressions plus importantes, la fugacité du soluté $\sigma$ en phase gaz est calculée à l'aide d'un coefficient de fugacité : $f_{\sigma }^{\text{g}}=x_{\sigma }^{\text{g}}\phi _{\sigma }^{\text{g}}P$ . Les équations de Krichevsky-Ilinskaya et Krichevsky-Kasarnovsky sont employées pour calculer des solubilités à haute pression, jusqu'à 1 000 bar environ^[33]^,^[35].

Mélanges multicomposants

On considère un mélange liquide composé de plusieurs solutés, notés $\sigma$ , et plusieurs solvants, notés $s$ ou $r$ , aux pression $P$ et température $T$ . Il est possible de calculer l'équilibre liquide-vapeur de ce mélange à partir des données d'équilibre de chacun des couples « soluté $\sigma$ - solvant $s$ ».

Lois des équilibres multicomposants

On note $f_{\sigma ,s}^{\text{l,*}}$ la fugacité du soluté $\sigma$ à l'état de liquide pur calculée à partir des propriétés du mélange binaire « soluté $\sigma$ - solvant $s$ » :

Pour tout couple soluté

\sigma

- solvant

s

f_{\sigma ,s}^{\text{l,*}}={k_{{\text{H}},\sigma ,s} \over \gamma _{\sigma ,s}^{{\text{l}},\infty }}

Si le soluté $\sigma$ n'existe pas à l'état de liquide pur dans les conditions de pression $P$ et température $T$ données du mélange, cette fugacité est fictive et sa valeur peut être différente d'un solvant $s$ à l'autre.

Pour les mélanges multicomposants, l'état de référence est l'état de dilution infinie de l'ensemble des solutés simultanément, c'est-à-dire le mélange de solvants en l'absence de tout soluté, ce mélange de solvants étant lui-même idéal^[36]. On définit les grandeurs $y_{i}^{\text{l}}$ , $f_{\sigma }^{\text{l,*}}$ et $\delta _{s}^{\text{l}}$ relatives à cet état. Une somme $\sum _{s}$ ou $\sum _{r}$ est effectuée sur l'ensemble des solvants du mélange, une somme $\sum _{\sigma }$ sur l'ensemble des solutés du mélange.

Pour tout corps

i

, soluté ou solvant :

y_{i}^{\text{l}}={x_{i}^{\text{l}} \over \sum _{s}x_{s}^{\text{l}}}

Avec $x_{i}^{\text{l}}$ la fraction molaire du corps $i$ dans le mélange multicomposant liquide. $y_{\sigma }^{\text{l}}$ est la quantité de soluté $\sigma$ rapportée à la quantité totale de solvants dans le mélange liquide. $y_{s}^{\text{l}}$ est la fraction molaire du solvant $s$ dans le mélange liquide des solvants seuls, autrement dit la limite de la fraction molaire $x_{s}^{\text{l}}$ du solvant $s$ à dilution infinie de tous les solutés du mélange liquide multicomposant ; on a $\sum _{s}y_{s}^{\text{l}}=1$ .

La fugacité $f_{\sigma }^{\text{l,*}}$ du soluté $\sigma$ à l'état de liquide pur est construite selon l'hypothèse du mélange idéal et peut être fictive :

Pour tout soluté

\sigma

\ln f_{\sigma }^{\text{l,*}}=\sum _{s}y_{s}^{\text{l}}\,\ln f_{\sigma ,s}^{\text{l,*}}

Pour tout solvant $s$ on pose le facteur correctif $\delta _{s}^{\text{l}}$ :

Pour tout solvant

s

\ln \delta _{s}^{\text{l}}=\sum _{\sigma }\sum _{r}y_{\sigma }^{\text{l}}y_{r}^{\text{l}}\,\ln {f_{\sigma ,s}^{\text{l,*}} \over f_{\sigma ,r}^{\text{l,*}}}=\sum _{\sigma }y_{\sigma }^{\text{l}}\left(\ln f_{\sigma ,s}^{\text{l,*}}-\ln f_{\sigma }^{\text{l,*}}\right)

Ce facteur intervient dans la correction de la loi de Raoult pour les solvants. On a $\sum _{s}x_{s}^{\text{l}}\ln \delta _{s}^{\text{l}}=0$ .

En présence d'un unique solvant $s$ on a $f_{\sigma }^{\text{l,*}}=f_{\sigma ,s}^{\text{l,*}}$ pour tout soluté $\sigma$ et $\ln \delta _{s}^{\text{l}}=0$ , soit $\delta _{s}^{\text{l}}=1$ . Si le soluté $\sigma$ existe à l'état de liquide pur dans les conditions de pression et température données, alors $f_{\sigma }^{\text{l,*}}$ n'est pas fictive et $f_{\sigma ,s}^{\text{l,*}}=f_{\sigma }^{\text{l,*}}$ pour tout solvant $s$ . Si tous les solutés $\sigma$ ont une fugacité $f_{\sigma }^{\text{l,*}}$ réelle, alors $\delta _{s}^{\text{l}}=1$ pour tout solvant $s$ . Dans un mélange liquide constitué uniquement de solvants, donc en l'absence de tout soluté, on a également $\delta _{s}^{\text{l}}=1$ pour tout solvant $s$ .

Pour un soluté $\sigma$ , l'équilibre liquide-vapeur est calculé par l'extension de la loi de Henry^[36] :

Extension de la loi de Henry aux mélanges multicomposants réels
pour un soluté

\sigma

x_{\sigma }^{\text{g}}\phi _{\sigma }^{\text{g}}P=x_{\sigma }^{\text{l}}\gamma _{\sigma }^{\text{l}}f_{\sigma }^{\text{l,*}}

Pour un solvant $s$ , l'équilibre liquide-vapeur est calculé par l'extension de la loi de Raoult^[36] :

Extension de la loi de Raoult aux mélanges multicomposants réels
pour un solvant

s

x_{s}^{\text{g}}\phi _{s}^{\text{g}}P=x_{s}^{\text{l}}\gamma _{s}^{\text{l}}\delta _{s}^{\text{l}}f_{s}^{\text{l,*}}

En application du théorème d'Euler, le volume molaire ${\bar {V}}^{\text{l}}$ de la phase liquide vaut :

{\begin{aligned}{{\bar {V}}^{\text{l}} \over RT}&={\sum _{\sigma }x_{\sigma }^{\text{l}}{\bar {V}}_{\sigma }^{\text{l}}+\sum _{s}x_{s}^{\text{l}}{\bar {V}}_{s}^{\text{l}} \over RT}=\sum _{\sigma }x_{\sigma }^{\text{l}}\left({\partial \ln f_{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}+\sum _{s}x_{s}^{\text{l}}\left({\partial \ln f_{s}^{\text{l}} \over \partial P}\right)_{T,n}\\&=\sum _{\sigma }x_{\sigma }^{\text{l}}\left[\sum _{s}y_{s}^{\text{l}}\left({{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty } \over RT}-\left({\partial \ln \gamma _{\sigma ,s}^{{\text{l}},\infty } \over \partial P}\right)_{T,n}\right)+\left({\partial \ln \gamma _{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}\right]+\sum _{s}x_{s}^{\text{l}}\left[{{\bar {V}}_{s}^{{\text{l}},*} \over RT}+\left({\partial \ln \gamma _{s}^{\text{l}} \over \partial P}\right)_{T,n}\right]\end{aligned}}

Le plus souvent, les modèles de coefficient d'activité $\gamma _{i}^{\text{l}}$ ne dépendent pas de la pression, le volume molaire est alors calculé selon le modèle idéal.

Volumes molaires partiels.

Le volume molaire partiel ${\bar {V}}_{\sigma }^{\text{l}}$ de tout soluté $\sigma$ vaut :

{\begin{aligned}{{\bar {V}}_{\sigma }^{\text{l}} \over RT}&=\left({\partial \ln f_{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}=\underbrace {\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}} _{\text{à composition constante = 0}}+\left({\partial \ln f_{\sigma }^{{\text{l}},*} \over \partial P}\right)_{T,n}+\left({\partial \ln \gamma _{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}\\&=\sum _{s}y_{s}^{\text{l}}\left({\partial \ln f_{\sigma ,s}^{{\text{l}},*} \over \partial P}\right)_{T,n}+\left({\partial \ln \gamma _{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}=\sum _{s}y_{s}^{\text{l}}\left(\left({\partial \ln k_{{\text{H}},\sigma ,s} \over \partial P}\right)_{T,n}-\left({\partial \gamma _{\sigma ,s}^{{\text{l}},\infty } \over \partial P}\right)_{T,n}\right)+\left({\partial \ln \gamma _{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}\\&=\sum _{s}y_{s}^{\text{l}}\left({{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty } \over RT}-\left({\partial \ln \gamma _{\sigma ,s}^{{\text{l}},\infty } \over \partial P}\right)_{T,n}\right)+\left({\partial \ln \gamma _{\sigma }^{\text{l}} \over \partial P}\right)_{T,n}\end{aligned}}

Le volume molaire partiel ${\bar {V}}_{s}^{\text{l}}$ de tout soluté $s$ vaut :

{\begin{aligned}{{\bar {V}}_{s}^{\text{l}} \over RT}&=\left({\partial \ln f_{s}^{\text{l}} \over \partial P}\right)_{T,n}=\underbrace {\left({\partial \ln x_{s}^{\text{l}} \over \partial P}\right)_{T,n}} _{\text{à composition constante = 0}}+\underbrace {\left({\partial \ln \!\left(\phi _{s}^{\text{g,*,sat}}P_{s}^{\text{sat}}\right) \over \partial P}\right)_{T,n}} _{\text{à température constante = 0}}+\left({\partial \ln {\mathcal {P}}_{s}^{{\text{l}},*} \over \partial P}\right)_{T,n}+\left({\partial \ln \delta _{s}^{\text{l}} \over \partial P}\right)_{T,n}+\left({\partial \ln \gamma _{s}^{\text{l}} \over \partial P}\right)_{T,n}\\&={{\bar {V}}_{s}^{{\text{l}},*} \over RT}+\left({\partial \ln \delta _{s}^{\text{l}} \over \partial P}\right)_{T,n}+\left({\partial \ln \gamma _{s}^{\text{l}} \over \partial P}\right)_{T,n}\end{aligned}}

avec :

\left({\partial \ln \delta _{s}^{\text{l}} \over \partial P}\right)_{T,n}=\sum _{\sigma }y_{\sigma }^{\text{l}}\left({{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty } \over RT}-\left({\partial \ln \gamma _{\sigma ,s}^{{\text{l}},\infty } \over \partial P}\right)_{T,n}\right)-\sum _{\sigma }\sum _{r}y_{\sigma }^{\text{l}}y_{r}^{\text{l}}\left({{\bar {V}}_{\sigma ,r}^{{\text{l}},\infty } \over RT}-\left({\partial \ln \gamma _{\sigma ,r}^{{\text{l}},\infty } \over \partial P}\right)_{T,n}\right)

Dans le calcul du volume molaire ${\bar {V}}^{\text{l}}$ , dans la sommation $\sum _{s}x_{s}^{\text{l}}{\bar {V}}_{s}^{\text{l}}$ il apparait le terme :

\sum _{s}x_{s}^{\text{l}}\left({\partial \ln \delta _{s}^{\text{l}} \over \partial P}\right)_{T,n}=\left({\partial \sum _{s}x_{s}^{\text{l}}\ln \delta _{s} \over \partial P}\right)_{T,n}=0

En effet :

\sum _{s}x_{s}^{\text{l}}\ln \delta _{s}^{\text{l}}=\sum _{s}\sum _{\sigma }x_{s}^{\text{l}}y_{\sigma }^{\text{l}}\ln f_{\sigma ,s}^{{\text{l}},*}-\sum _{s}\sum _{\sigma }\sum _{r}x_{s}^{\text{l}}y_{\sigma }^{\text{l}}y_{r}^{\text{l}}\ln f_{\sigma ,r}^{{\text{l}},*}

or $x_{s}^{\text{l}}y_{r}^{\text{l}}=y_{s}^{\text{l}}x_{r}^{\text{l}}$ , on a donc :

{\begin{aligned}\sum _{s}x_{s}^{\text{l}}\ln \delta _{s}^{\text{l}}&=\sum _{s}\sum _{\sigma }x_{s}^{\text{l}}y_{\sigma }^{\text{l}}\ln f_{\sigma ,s}^{{\text{l}},*}-\sum _{s}\sum _{\sigma }\sum _{r}y_{s}^{\text{l}}x_{r}^{\text{l}}y_{\sigma }^{\text{l}}\ln f_{\sigma ,r}^{{\text{l}},*}=\sum _{s}\sum _{\sigma }x_{s}^{\text{l}}y_{\sigma }^{\text{l}}\ln f_{\sigma ,s}^{{\text{l}},*}-\underbrace {\left(\sum _{s}y_{s}^{\text{l}}\right)} _{=1}\sum _{\sigma }\sum _{r}x_{r}^{\text{l}}y_{\sigma }^{\text{l}}\ln f_{\sigma ,r}^{{\text{l}},*}\\&=\sum _{s}\sum _{\sigma }x_{s}^{\text{l}}y_{\sigma }^{\text{l}}\ln f_{\sigma ,s}^{{\text{l}},*}-\sum _{\sigma }\sum _{r}x_{r}^{\text{l}}y_{\sigma }^{\text{l}}\ln f_{\sigma ,r}^{{\text{l}},*}=0\end{aligned}}

Lois des équilibres multicomposants idéaux

Comme pour un mélange binaire, la fugacité (fictive pour les gaz) $f_{\sigma }^{\text{l,*}}$ du soluté $\sigma$ à l'état de liquide pur est supposée calculée selon la relation :

f_{\sigma }^{\text{l,*}}={k_{{\text{H}},\sigma ,m} \over \gamma _{\sigma ,m}^{{\text{l}},\infty }}

avec :

$k_{{\text{H}},\sigma ,m}$ la constante de Henry du soluté $\sigma$ dans le mélange liquide ;
$\gamma _{\sigma ,m}^{{\text{l}},\infty }$ le coefficient d'activité du soluté $\sigma$ à dilution infinie dans le mélange liquide.

En supposant que le mélange liquide est idéal, on a $\gamma _{\sigma ,m}^{{\text{l}},\infty }=\gamma _{\sigma ,s}^{{\text{l}},\infty }=\gamma _{\sigma }^{\text{l}}=\gamma _{s}^{\text{l}}=1$ pour tout soluté $\sigma$ et tout solvant $s$ . La relation $\ln f_{\sigma }^{\text{l,*}}=\sum _{s}y_{s}^{\text{l}}\,\ln f_{\sigma ,s}^{\text{l,*}}$ donne pour tout soluté $\sigma$ la relation idéale de Krichevsky^[36] :

Équation de Krichevsky

\ln k_{{\text{H}},\sigma ,m}=\sum _{r}y_{r}^{\text{l}}\ln k_{{\text{H}},\sigma ,r}

On a également pour tout solvant $s$ :

\ln \delta _{s}^{\text{l}}=\sum _{\sigma }\sum _{r}y_{\sigma }^{\text{l}}y_{r}^{\text{l}}\ln {k_{{\text{H}},\sigma ,s} \over k_{{\text{H}},\sigma ,r}}

Pour des pressions proches de la pression atmosphérique (moins de 10 bar) le gaz se comporte comme un gaz parfait, soit $\phi _{\sigma }^{\text{g}}=\phi _{s}^{\text{g}}=\phi _{s}^{\text{g,*,sat}}=1$ . Pour les phases liquides idéales et les basses pressions on a par conséquent les lois idéales :

Loi de Henry étendue aux mélanges multicomposants idéaux pour un soluté

\sigma

x_{\sigma }^{\text{g}}P=x_{\sigma }^{\text{l}}k_{{\text{H}},\sigma ,m}

et :

Loi de Raoult étendue aux mélanges multicomposants idéaux pour un solvant

s

x_{s}^{\text{g}}P=x_{s}^{\text{l}}\delta _{s}^{\text{l}}P_{s}^{\text{sat}}{\mathcal {P}}_{s}^{{\text{l}},*}

Le volume molaire ${\bar {V}}^{\text{l,id}}$ de la phase liquide idéale vaut :

{\bar {V}}^{\text{l,id}}=\sum _{\sigma }\sum _{s}x_{\sigma }^{\text{l}}y_{s}^{\text{l}}{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }+\sum _{s}x_{s}^{\text{l}}{\bar {V}}_{s}^{{\text{l}},*}

Application à un mélange ternaire : un soluté et deux solvants

On considère un mélange liquide ternaire constitué d'un soluté $\sigma$ et de deux solvants, notés $s1$ et $s2$ . Soient les coefficients d'activité du soluté $\sigma$ à dilution infinie dans chacun des deux solvants $s1$ et $s2$ selon le modèle de Margules :

{\displaystyle \ln \gamma _{\sigma ,s1}^{{\text{l}},\infty }=A_{\sigma ,s1}\quad

On suppose que l'enthalpie libre molaire d'excès ${\bar {G}}^{\text{E}}$ du mélange ternaire est calculable selon l'extension du modèle de Margules^[37] :

{\mathcal {G}}^{\text{E}}={{\bar {G}}^{\text{E}} \over RT}=A_{\sigma ,s1}\,x_{\sigma }^{\text{l}}x_{s1}^{\text{l}}+A_{\sigma ,s2}\,x_{\sigma }^{\text{l}}x_{s2}^{\text{l}}+A_{s1,s2}\,x_{s1}^{\text{l}}x_{s2}^{\text{l}}

Les coefficients d'activité des trois corps sont donnés par^[36] :

coefficients d'activité

\ln \gamma _{\sigma }^{\text{l}}=A_{\sigma ,s1}\,x_{s1}^{\text{l}}+A_{\sigma ,s2}\,x_{s2}^{\text{l}}-{\mathcal {G}}^{\text{E}}

\ln \gamma _{s1}^{\text{l}}=A_{\sigma ,s1}\,x_{\sigma }^{\text{l}}+A_{s1,s2}\,x_{s2}^{\text{l}}-{\mathcal {G}}^{\text{E}}

\ln \gamma _{s2}^{\text{l}}=A_{\sigma ,s2}\,x_{\sigma }^{\text{l}}+A_{s1,s2}\,x_{s1}^{\text{l}}-{\mathcal {G}}^{\text{E}}

On pose :

{\displaystyle y_{\sigma }^{\text{l}}={x_{\sigma }^{\text{l}} \over x_{s1}^{\text{l}}+x_{s2}^{\text{l}}}\quad

À dilution infinie du soluté $\sigma$ , soit $x_{\sigma }^{\text{l}}\to 0$ , on a les limites :

{\displaystyle x_{s1}^{\text{l}}\to y_{s1}^{\text{l}}\quad

{\mathcal {G}}^{\text{E}}\to {\mathcal {G}}_{\text{solvant}}^{\text{E}}={{\bar {G}}_{\text{solvant}}^{\text{E}} \over RT}=A_{s1,s2}\,y_{s1}^{\text{l}}y_{s2}^{\text{l}}

\ln \gamma _{\sigma }^{\text{l}}\to \ln \gamma _{\sigma ,m}^{{\text{l}},\infty }=A_{\sigma ,s1}\,y_{s1}^{\text{l}}+A_{\sigma ,s2}\,y_{s2}^{\text{l}}-A_{s1,s2}\,y_{s1}^{\text{l}}y_{s2}^{\text{l}}=y_{s1}^{\text{l}}\,\ln \gamma _{\sigma ,s1}^{{\text{l}},\infty }+y_{s2}^{\text{l}}\,\ln \gamma _{\sigma ,s2}^{{\text{l}},\infty }-{\mathcal {G}}_{\text{solvant}}^{\text{E}}

avec ${\bar {G}}_{\text{solvant}}^{\text{E}}$ l'enthalpie libre molaire d'excès du mélange de solvants en l'absence de soluté $\sigma$ .

La fugacité $f_{\sigma }^{\text{l,*}}$ du soluté $\sigma$ à l'état de liquide pur est calculée selon^[36] :

\ln f_{\sigma }^{\text{l,*}}=\ln {k_{{\text{H}},\sigma ,m} \over \gamma _{\sigma ,m}^{{\text{l}},\infty }}=y_{s1}^{\text{l}}\,\ln f_{\sigma ,s1}^{\text{l,*}}+y_{s2}^{\text{l}}\,\ln f_{\sigma ,s2}^{\text{l,*}}=y_{s1}^{\text{l}}\,\ln {k_{{\text{H}},\sigma ,s1} \over \gamma _{\sigma ,s1}^{{\text{l}},\infty }}+y_{s2}^{\text{l}}\,\ln {k_{{\text{H}},\sigma ,s2} \over \gamma _{\sigma ,s2}^{{\text{l}},\infty }}

d'où :

pour le soluté

\sigma

\ln f_{\sigma }^{\text{l,*}}=y_{s1}^{\text{l}}\left(\ln k_{{\text{H}},\sigma ,s1}-A_{\sigma ,s1}\right)+y_{s2}^{\text{l}}\left(\ln k_{{\text{H}},\sigma ,s2}-A_{\sigma ,s2}\right)

et la constante de Henry $k_{{\text{H}},\sigma ,m}$ du soluté $\sigma$ dans le mélange ternaire :

\ln k_{{\text{H}},\sigma ,m}=y_{s1}^{\text{l}}\,\ln k_{{\text{H}},\sigma ,s1}+y_{s2}^{\text{l}}\,\ln k_{{\text{H}},\sigma ,s2}-{\mathcal {G}}_{\text{solvant}}^{\text{E}}

Ainsi, lorsque le mélange de solvants est idéal, soit $A_{s1,s2}=0$ et ${\mathcal {G}}_{\text{solvant}}^{\text{E}}=0$ , on retrouve l'équation idéale de Krichevsky.

Pour les deux solvants $s1$ et $s2$ on a :

\ln \delta _{s1}^{\text{l}}=y_{\sigma }^{\text{l}}y_{s2}^{\text{l}}\,\ln {f_{\sigma ,s1}^{\text{l,*}} \over f_{\sigma ,s2}^{\text{l,*}}}=y_{\sigma }^{\text{l}}y_{s2}^{\text{l}}\,\ln \!\left({k_{{\text{H}},\sigma ,s1} \over k_{{\text{H}},\sigma ,s2}}{\gamma _{\sigma ,s2}^{{\text{l}},\infty } \over \gamma _{\sigma ,s1}^{{\text{l}},\infty }}\right)

\ln \delta _{s2}^{\text{l}}=y_{\sigma }^{\text{l}}y_{s1}^{\text{l}}\,\ln {f_{\sigma ,s2}^{\text{l,*}} \over f_{\sigma ,s1}^{\text{l,*}}}=y_{\sigma }^{\text{l}}y_{s1}^{\text{l}}\,\ln \!\left({k_{{\text{H}},\sigma ,s2} \over k_{{\text{H}},\sigma ,s1}}{\gamma _{\sigma ,s1}^{{\text{l}},\infty } \over \gamma _{\sigma ,s2}^{{\text{l}},\infty }}\right)

d'où :

pour les deux solvants

s1

s2

\ln \delta _{s1}^{\text{l}}=y_{\sigma }^{\text{l}}y_{s2}^{\text{l}}\,\left(\ln {k_{{\text{H}},\sigma ,s1} \over k_{{\text{H}},\sigma ,s2}}+A_{\sigma ,s2}-A_{\sigma ,s1}\right)

\ln \delta _{s2}^{\text{l}}=y_{\sigma }^{\text{l}}y_{s1}^{\text{l}}\,\left(\ln {k_{{\text{H}},\sigma ,s2} \over k_{{\text{H}},\sigma ,s1}}+A_{\sigma ,s1}-A_{\sigma ,s2}\right)

Ces expressions peuvent être étendues à des mélanges contenant plus de solutés et de solvants, avec ${\mathcal {G}}^{\text{E}}=\sum _{i}\sum _{j>i}A_{i,j}\,x_{i}^{\text{l}}x_{j}^{\text{l}}$ . Il est alors pratique de négliger les interactions entre solutés si ceux-ci ne sont que faiblement concentrés, soit $A_{i,j}=0$ si $i$ et $j$ sont deux solutés :

{\mathcal {G}}^{\text{E}}=\sum _{\sigma }\sum _{s}A_{\sigma ,s}\,x_{\sigma }^{\text{l}}x_{s}^{\text{l}}+\sum _{s}\sum _{r>s}A_{s,r}\,x_{s}^{\text{l}}x_{r}^{\text{l}}

Applications

Étude de la solubilité

La loi de Henry permet d'établir l'évolution de la solubilité $x_{\sigma }^{\text{l}}$ en fonction de la pression et de la température dans ses limites d'application, pour rappel aux basses pressions et faibles solubilités.

En fonction de la pression

En dérivant, à température constante, l'expression de la loi de Henry par rapport à la pression, on obtient :

\left({\partial \ln P_{\sigma } \over \partial P}\right)_{T}=\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial P}\right)_{T}+\left({\partial \ln k_{{\text{H}},\sigma ,s} \over \partial P}\right)_{T}=\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial P}\right)_{T}+{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty } \over RT}

avec ${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ le volume molaire partiel du soluté $\sigma$ à dilution infinie dans le solvant $s$ (voir le paragraphe Constante de Henry - Dépendance à la pression).

Cas de la pression partielle constante

Si la pression partielle $P_{\sigma }$ du soluté est maintenue constante et que l'on fait varier la pression totale $P$ par l'intermédiaire d'un tiers corps gazeux incondensable (non soluble dans le liquide), alors :

\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial P}\right)_{T}=-{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty } \over RT}

En conséquence, si ${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ est positif, c'est-à-dire si le volume du liquide augmente lors d'une dissolution de soluté $\sigma$ , la solubilité $x_{\sigma }^{\text{l}}$ diminue si la pression totale $P$ augmente à pression partielle $P_{\sigma }$ du soluté constante.

Cas du soluté seul en phase gaz

Si le soluté est seul en phase gaz, en l'absence d'inerte et le solvant $s$ n'étant pas volatil, la pression partielle $P_{\sigma }$ du soluté est égale à la pression totale $P$ , soit $P_{\sigma }=P$ , alors :

\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial P}\right)_{T}={1 \over P}-{{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty } \over RT}

En application de la loi des gaz parfaits, aux basses pressions le volume molaire de la phase gaz vaut : ${\bar {V}}^{\bullet }=RT/P$ . D'autre part, toujours aux basses pressions, le volume molaire de la phase gaz est très supérieur à celui d'un volume molaire partiel en phase liquide, soit ${\bar {V}}^{\bullet }\gg {\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ , d'où :

Aux basses pressions :

\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial P}\right)_{T}\approx {{\bar {V}}^{\bullet } \over RT}={1 \over P}

Avec un point de solubilité connu $\left(x_{\sigma }^{{\text{l}},\circ },P^{\circ },T\right)$ on intègre à température constante :

{x_{\sigma }^{\text{l}} \over x_{\sigma }^{{\text{l}},\circ }}={P \over P^{\circ }}

Aux basses pressions, la solubilité $x_{\sigma }^{\text{l}}$ augmente linéairement avec la pression totale $P$ lorsque le soluté $\sigma$ est seul en phase gaz.

Le volume molaire d'un gaz diminue avec une augmentation de pression. Aux pressions élevées, lorsque le modèle des gaz parfaits ne s'applique plus, le volume molaire partiel ${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ n'est plus négligeable devant le volume molaire du gaz. On considère l'équation de Krichevsky-Ilinskaya (voir le paragraphe Mélanges binaires). Si seul le soluté $\sigma$ se trouve en phase gaz, sa fugacité dans cette phase varie en fonction de la pression selon :

\left({\partial \ln f_{\sigma }^{\text{g}} \over \partial P}\right)_{T}={{\bar {V}}_{\sigma }^{{\text{g}},*} \over RT}

avec ${\bar {V}}_{\sigma }^{{\text{g}},*}$ le volume molaire du soluté pur à l'état gazeux dans les conditions de pression et température du mélange. On peut considérer que le volume molaire partiel en phase liquide ${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ est indépendant de la pression. L'équation de Krichevsky-Ilinskaya donne par conséquent^[38]^,^[39] :

Aux hautes pressions :

\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial P}\right)_{T}={{\bar {V}}_{\sigma }^{{\text{g}},*}-{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty } \over RT}

Lorsque ${\bar {V}}_{\sigma }^{{\text{g}},*}>{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ , aux basses pressions, la solubilité augmente avec la pression, elle décroît lorsque ${\bar {V}}_{\sigma }^{{\text{g}},*}<{\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ aux très hautes pressions (lorsque le volume molaire de la phase gaz est faible). Ainsi, lorsque ${\bar {V}}_{\sigma }^{{\text{g}},*}={\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ la solubilité $x_{\sigma }^{\text{l}}$ atteint un maximum en fonction de la pression. Ceci a été vérifié expérimentalement pour la solubilité de l'azote dans l'eau, qui atteint à 18 °C un maximum à environ 3 000 atm^[38]^,^[39].

En fonction de la température

Solubilité du dioxyde de carbone dans l'eau en fonction de la température à pression atmosphérique^[40].

En dérivant, à pression constante, l'expression de la loi de Henry par rapport à la température, on obtient :

\left({\partial \ln P_{\sigma } \over \partial {1 \over T}}\right)_{P}=\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial {1 \over T}}\right)_{P}+\left({\partial \ln k_{{\text{H}},\sigma ,s} \over \partial {1 \over T}}\right)_{P}=\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial {1 \over T}}\right)_{P}+{\Delta _{\text{sol}}H_{\sigma ,s} \over R}

avec $\Delta _{\text{sol}}H_{\sigma ,s}$ l'enthalpie de dissolution du soluté $\sigma$ dans le solvant $s$ (voir le paragraphe Constante de Henry - Dépendance à la température).

Que la pression partielle $P_{\sigma }$ du soluté soit maintenue constante, ou que la phase gaz soit constituée du soluté $\sigma$ seul, auquel cas $P_{\sigma }=P$ , on obtient^[41] :

\left({\partial \ln x_{\sigma }^{\text{l}} \over \partial {1 \over T}}\right)_{P}=-{\Delta _{\text{sol}}H_{\sigma ,s} \over R}

Diverses formes de la solubilité en fonction de la température sont communément employées^[21]^,^[23] :

\ln x_{\sigma }^{\text{l}}=a+{b \over T}+c\,\ln T+d\,T

\ln x_{\sigma }^{\text{l}}=a+{b \over T}+{c \over T^{2}}+{d \over T^{3}}

avec $a$ , $b$ , $c$ et $d$ des constantes empiriques spécifiques du couple « soluté $\sigma$ - solvant $s$ ».

Aux basses pressions et températures, pour la plupart des gaz la dissolution est exothermique, soit $\Delta _{\text{sol}}H_{\sigma ,s}<0$ , par conséquent la solubilité diminue lorsque la température augmente^[19]. De nombreux gaz présentent un minimum de solubilité, la solubilité augmentant après avoir diminué lorsque la température augmente^[42]^,^[43]. Ainsi, aux basses pressions, le minimum de solubilité de l'hélium dans l'eau se situe à environ 30 °C, ceux de l'argon, de l'oxygène et de l'azote se situent entre 92 et 93 °C et celui du xénon à environ 114 °C^[44].

Pressurisation des boissons gazeuses

En ouvrant une bouteille de champagne la pression chute brutalement dans la bouteille et, selon la loi de Henry, la solubilité du gaz diminue. Le dioxyde de carbone (CO₂) dissout dans le vin se désorbe et forme des bulles dans le liquide.

Les boissons gazeuses sont maintenues sous une pression importante de dioxyde de carbone (CO₂). On suppose qu'il n'y a que du CO₂ dans le gaz, soit $x_{{\text{CO}}_{2}}^{\text{g}}=1$ , la présence d'eau en phase gaz étant négligeable, soit $x_{{\text{H}}_{2}{\text{O}}}^{\text{g}}\approx 0$ . La pression partielle du CO₂ vaut alors la pression totale : $P_{{\text{CO}}_{2}}=x_{{\text{CO}}_{2}}^{\text{g}}P=P$ . Cette pression permet de dissoudre une grande quantité de gaz dans le liquide en vertu de la loi de Henry :

P_{{\text{CO}}_{2}}=x_{{\text{CO}}_{2}}^{\text{l}}k_{{\text{H,CO}}_{2},{\text{boisson}}}

En ouvrant la bouteille la pression $P_{{\text{CO}}_{2}}$ chute brusquement. Puisque $k_{{\text{H,CO}}_{2},{\text{boisson}}}$ est quasi constante, alors $x_{{\text{CO}}_{2}}^{\text{l}}$ ne peut que diminuer : la solubilité du dioxyde de carbone chute. En conséquence, le CO₂ dissout se désorbe en formant des bulles dans le liquide^[5]^,^[45].

Solubilité des gaz atmosphériques dans le sang

La composition de l'atmosphère est considérée comme constante : elle contient environ 20,9 % molaire d'oxygène O₂ et d'autres gaz dont l'azote N₂ très majoritaire, soit les fractions molaires $x_{{\text{O}}_{2}}^{\text{g}}$ = 0,209 et $x_{{\text{N}}_{2}}^{\text{g}}$ ≈ 0,791. Les pressions partielles d'oxygène $P_{{\text{O}}_{2}}$ et d'azote $P_{{\text{N}}_{2}}$ varient donc en proportion de la pression atmosphérique totale $P$ selon :

P_{{\text{O}}_{2}}=x_{{\text{O}}_{2}}^{\text{g}}P

P_{{\text{N}}_{2}}=x_{{\text{N}}_{2}}^{\text{g}}P

Les teneurs en oxygène et azote dissouts dans le sang, $x_{{\text{O}}_{2}}^{\text{l}}$ et $x_{{\text{N}}_{2}}^{\text{l}}$ , répondent à la loi de Henry et dépendent par conséquent directement de la pression atmosphérique :

x_{{\text{O}}_{2}}^{\text{g}}P=x_{{\text{O}}_{2}}^{\text{l}}k_{{\text{H,O}}_{2},{\text{sang}}}

x_{{\text{N}}_{2}}^{\text{g}}P=x_{{\text{N}}_{2}}^{\text{l}}k_{{\text{H,N}}_{2},{\text{sang}}}

En altitude, par exemple en montagne, la pression atmosphérique $P$ est plus basse qu'au niveau de la mer. La pression partielle en oxygène $P_{{\text{O}}_{2}}$ y est donc plus faible. En conséquence de la loi de Henry, la teneur en oxygène dissout dans le sang, $x_{{\text{O}}_{2}}^{\text{l}}$ , est plus basse en montagne qu'à des altitudes moins élevées. Cet état est appelé hypoxie et peut provoquer le mal aigu des montagnes si ces altitudes sont atteintes trop rapidement, sans acclimatation progressive (par exemple à l'atterrissage en montagne d'un avion parti du niveau de la mer)^[46].

Au contraire, sous l'eau la pression est plus importante qu'au niveau de la surface. En un point où la pression $P$ est le double de la pression atmosphérique standard (c'est le cas à 10 m de profondeur), les solubilités des gaz, $x_{{\text{O}}_{2}}^{\text{l}}$ et $x_{{\text{N}}_{2}}^{\text{l}}$ , sont doublées par rapport à la surface. Un plongeur consomme l'oxygène mais stocke l'azote de l'air dissout dans son organisme. Lorsque le plongeur remonte vers la surface l'azote se désorbe en raison de la baisse de pression. Un accident de décompression survient si la remontée est trop rapide : le plongeur ne peut évacuer ce gaz par la respiration et l'azote forme des bulles dans le sang. Les bulles ainsi créées se dilatent dans les vaisseaux sanguins, toujours en raison de la baisse de pression (loi de Boyle-Mariotte), et peuvent provoquer une embolie gazeuse et le décès du plongeur^[5]^,^[47].

Constantes de Henry pour des gaz dissouts dans l'eau

Le tableau suivant donne quelques valeurs de la constante de Henry pour des gaz dissouts dans l'eau à 25 °C (298,15 K)^[7].

Valeurs de la constante de Henry
pour des gaz dissouts dans l'eau à 298,15 K^[7].
Équation	$k_{\mathrm {H} }^{\text{pc}}={P \over c_{\text{aq}}}$	$H^{\text{cp}}={c_{\text{aq}} \over P}$	$k_{\mathrm {H} }^{\text{px}}={P \over x}$	$H^{\text{cc}}={c_{\text{aq}} \over c_{\text{gas}}}$
Unité	${\mathsf {l\cdot atm \over mol}}$	${\mathsf {mol \over l\cdot atm}}$	${\mathsf {atm}}$	sans dimension
Oxygène (O₂)	769,23	1,3×10⁻³	4,259×10⁴	3,181×10^-2
Hydrogène (H₂)	1282,05	7,8×10^-4	7,099×10⁴	1,907×10^-2
Dioxyde de carbone (CO₂)	29,41	3,4×10^-2	0,163×10⁴	0,8317
Azote (N₂)	1639,34	6,1×10^-4	9,077×10⁴	1,492×10^-2
Hélium (He)	2702,7	3,7×10^-4	14,97×10⁴	9,051×10^-3
Néon (Ne)	2222,22	4,5×10^-4	12,30×10⁴	1,101×10^-2
Argon (Ar)	714,28	1,4×10^-3	3,955×10⁴	3,425×10^-2
Monoxyde de carbone (CO)	1052,63	9,5×10^-4	5,828×10⁴	2,324×10^-2

Avec :

$c_{\text{aq}}$ la concentration du gaz en solution aqueuse (mol/l) ;
$c_{\text{gaz}}$ la concentration du gaz en phase vapeur (mol/l) ;
$P$ la pression partielle du gaz en phase vapeur (atm) ;
$x$ la fraction molaire du gaz en solution aqueuse (sans dimension).

Notations

Alphabet latin

$A$ le paramètre du modèle d'activité de Margules ;
$f_{i}^{\text{g}}$ la fugacité du corps $i$ en phase vapeur ;
$f_{i}^{\text{l}}$ la fugacité du corps $i$ en phase liquide ;
$f_{i}^{{\text{l}},*}$ la fugacité du corps $i$ liquide pur ;
${\bar {H}}_{\sigma ,s}^{{\text{l}},\infty }$ l'enthalpie molaire partielle du soluté $\sigma$ à dilution infinie dans le solvant $s$ ;
${\bar {H}}_{\sigma }^{\bullet ,*}$ l'enthalpie molaire du soluté $\sigma$ à l'état de gaz parfait pur ;
$k_{{\text{H}},\sigma ,s}$ la constante de Henry du soluté $\sigma$ dans le solvant $s$ ;
$k_{{\text{H}},\sigma ,s}^{\circ }$ la constante de Henry du soluté $\sigma$ dans le solvant $s$ à $P_{s}^{\text{sat}}$ ;
$k_{{\text{H}},\sigma ,m}$ la constante de Henry du soluté $\sigma$ dans un mélange liquide multicomposant ;
$P$ la pression ;
$P_{i}$ la pression partielle du corps $i$ ;
$P_{s}^{\text{sat}}$ la pression de vapeur saturante du solvant $s$ ;
${\mathcal {P}}_{\sigma ,s}^{{\text{l}},\infty }$ le facteur de Poynting du soluté $\sigma$ à dilution infinie dans le solvant $s$ liquide ;
${\mathcal {P}}_{s}^{{\text{l}},*}$ le facteur de Poynting du solvant $s$ liquide pur ;
$R$ la constante universelle des gaz parfaits ;
$T$ la température ;
${\bar {V}}_{\sigma }^{{\text{g}},*}$ le volume molaire du soluté $\sigma$ gazeux pur ;
$V^{\text{l}}$ le volume de la solution liquide ;
${\bar {V}}^{\text{l}}$ le volume molaire de la solution liquide ;
${\bar {V}}_{i}^{\text{l}}$ le volume molaire partiel du corps $i$ dans le mélange liquide ;
${\bar {V}}_{\sigma ,s}^{{\text{l}},\infty }$ le volume molaire partiel du soluté $\sigma$ à dilution infinie dans le solvant $s$ liquide ;
${\bar {V}}_{s}^{{\text{l}},*}$ le volume molaire du solvant $s$ liquide pur ;
$x_{i}^{\text{g}}$ la fraction molaire du corps $i$ en phase gaz ;
$x_{i}^{\text{l}}$ la fraction molaire du corps $i$ en phase liquide ;
$y_{i}^{\text{l}}$ la quantité du corps $i$ rapportée à la quantité totale de solvants dans un mélange liquide multicomposant.

Alphabet grec

$\gamma _{i}^{\text{l}}$ le coefficient d'activité du corps $i$ en phase liquide ;
$\gamma _{\sigma ,m}^{{\text{l}},\infty }$ le coefficient d'activité du soluté $\sigma$ à dilution infinie dans un mélange multicomposant liquide ;
$\gamma _{\sigma ,s}^{{\text{l}},\infty }$ le coefficient d'activité du soluté $\sigma$ à dilution infinie dans le solvant $s$ liquide ;
$\delta _{s}^{\text{l}}$ le coefficient d'ajustement de la loi de Raoult pour le solvant $s$ dans un mélange multicomposant liquide ;
$\Delta _{\text{sol}}H_{\sigma ,s}$ l'enthalpie de dissolution du soluté $\sigma$ dans le solvant $s$ ;
$\phi _{i}^{\text{g}}$ le coefficient de fugacité du corps $i$ en phase gaz ;
$\phi _{\sigma }^{\text{l}}$ le coefficient de fugacité du soluté $\sigma$ en phase liquide ;
$\phi _{s}^{\text{g,*,sat}}$ le coefficient de fugacité du solvant $s$ pur en phase gaz à $P_{s}^{\text{sat}}$ .

Notes et références

Notes

↑ (en) William Henry, « Experiments on the quantity of gases absorbed by water, at different temperatures, and under different pressures », Philosophical Transansactions of the Royal Society of London, vol. 93,‎ 1803, p. 29–274 (DOI 10.1098/rstl.1803.0004).
1 2 Peter William Atkins et Paul Depovere (trad. de l'anglais par Monique Mottet), Éléments de chimie physique, Paris, Bruxelles, De Boeck Supérieur, 1998, 512 p. (ISBN 2-7445-0010-0, lire en ligne), p. 133.
1 2 3 4 Henri Fauduet, Principes fondamentaux du génie des procédés et de la technologie chimique, Lavoisier, 2012, 2^e éd., 800 p. (ISBN 9782744500107, lire en ligne), p. 164.
1 2 3 (en) Quantities, Units and Symbols in Physical Chemistry (Green Book), Cambridge, Union internationale de chimie pure et appliquée, 2007, 3^e éd. (1^re éd. 1988), 250 p. (ISBN 978-0-85404-433-7, présentation en ligne, lire en ligne [PDF]), p. 58.
1 2 3 John C. Kotz et Paul M. Treichel Jr (trad. de l'anglais), Chimie des solutions, Bruxelles/Issy-les-Moulineaux, De Boeck Supérieur, coll. « Chimie générale », 2006, 356 p. (ISBN 978-2-8041-5232-1, lire en ligne), p. 20.
↑ Johan Wouters, Concentré de CHIMIE, Presses universitaires de Namur, 2014, 398 p. (ISBN 9782870378526, lire en ligne), p. 134.
1 2 3 4 5 6 7 (en) « Henry's law constants » (consulté le 10 janvier 2020). Une compilation de constantes de Henry pour les solutions aqueuses, dont : (en) « Compilation of Henry’s law constants (version 4.0) for water as solvent » [PDF], sur Atmospheric Chemistry and Physics (consulté le 10 janvier 2020).
1 2 O'Connell 2005, p. 435.
1 2 Jean-Pierre-Corriou, Thermodynamique chimique : Diagrammes thermodynamiques, vol. J 1 026, Éditions techniques de l'ingénieur, 1985 (lire en ligne), p. 25-26.
↑ Vidal 1997, p. 168.
1 2 Tosun 2012, p. 450.
1 2 3 4 5 Wilhelm 2012, p. 65.
1 2 3 4 5 6 7 8 9 Corriou 1985, p. 4.
1 2 3 Wilhelm 2012, p. 66.
1 2 3 4 5 Wilhelm 2012, p. 70.
1 2 3 Tosun 2012, p. 462.
1 2 3 4 5 Coquelet et al. 2007, p. 6.
↑ (en) S. W. Brelvi et J. P. O'Connell, « Corresponding States Correlations for Liquid Compressibility and Partial Molal Volumes of Gases at Infinite Dilution in Liquids », AIChE Journal, vol. 18, n^o 6,‎ 1972, p. 1239-1243 (lire en ligne, consulté le 10 janvier 2020).
1 2 3 4 5 6 7 Tosun 2012, p. 466.
↑ L'indice ${\text{sol}}$ est préconisé par le Green Book 2007, p. 60.
1 2 3 (en) John J. Caroll, « Henry's Law Revisited », Chemical Engineering Progress,‎ 1999, p. 54 (lire en ligne [PDF], consulté le 10 janvier 2020).
1 2 3 4 Vidal 1997, p. 295.
1 2 3 4 5 (en) Trevor M. Letcher, Rubin Battino et H. Lawrence Clever, Development and Applications in Solubility, Royal Society of Chemistry, 2007, 414 p. (ISBN 9780854043729, lire en ligne), p. 70-71.
↑ Vidal 1997, p. 195.
1 2 3 Vidal 1997, p. 209-210.
1 2 Prausnitz et al. 1999, p. 586.
↑ Marc Blétry et Marc Presset, Chimie des solutions : De l'élémentaire aux calculs numériques, Louvain-la-Neuve, De Boeck Superieur, 2019, 480 p. (ISBN 978-2-8073-2305-6, lire en ligne), p. 366.
↑ Tosun 2012, p. 465.
1 2 Wilhelm 2012, p. 75.
↑ Prausnitz et al. 1999, p. 592.
↑ Drew et al. 1968, p. 169.
↑ (en) Alice Wu, John J. Carroll, Mingqiang Hao et Weiyao Zhu, Gas Injection into Geological Formations and Related Topics, John Wiley & Sons, 2020, 384 p. (ISBN 9781119593331, lire en ligne), p. 67.
1 2 Drew et al. 1968, p. 167.
↑ Prausnitz et al. 1999, p. 589.
↑ Prausnitz et al. 1999, p. 590.
1 2 3 4 5 6 Van Ness et al. 1979.
↑ Prausnitz et al. 1999, p. 613.
1 2 (en) I. R. Krichevsky, « The Existence of a Maximum in the Gas Solubility—Pressure Curve », J. Am. Chem. Soc., vol. 59, n^o 3,‎ mars 1936, p. 595–596 (lire en ligne, consulté le 24 août 2020).
1 2 Drew et al. 1968, p. 168-169.
↑ Ce graphe et d'autres exemples sur : (en) « Solubility of Gases in Water », sur engineeringtoolbox.com (consulté le 9 mai 2020).
↑ Prausnitz et al. 1999, p. 596.
↑ (en) Thomas B. Drew, Giles R. Cokelet, John W. Hoopes et Theodore Vermeulen, Advances in Chemical Engineering, vol. 11, Academic Press, 1981, 451 p. (ISBN 9780080565583, lire en ligne), p. 23.
↑ (en) Nobuo Maeda, Nucleation of Gas Hydrates, Springer Nature, 2020 (ISBN 9783030518745, lire en ligne), p. 135.
↑ (en) Paul Cohen, The ASME Handbook on Water Technology for Thermal Power Systems, The American Society of Mechanical Engineers, 1989, 1828 p. (ISBN 978-0-7918-0634-0, lire en ligne), p. 442.
↑ Gérard Liger-Belair, Clara Cilindre, Marielle Bourget, Hervé Pron, Fabien Beaumont, Guillaume Polidori, Philippe Jamesse, Miguel Cabral et Paulo Lopes, « La perception du CO2 dans les vins effervescents : Un univers multisensoriel spécifique et ses influences sur les sensations gustatives - Apports possibles des neurosciences », Revue des Œnologues, vol. 155,‎ 2015, p. 47-52 (lire en ligne, consulté le 15 décembre 2020).
↑ Samuel Vergès, « Quelles réponses au manque d'oxygène en altitude ? », sur Le Figaro.fr, 1^er février 2012 (consulté le 15 décembre 2020).
↑ Francis Héritier, M. Paul Avanzi et Laurent Nicod, « Poumons et plongée subaquatique », Revue médicale suisse, vol. 451, n^o 10,‎ 2014, p. 2182-2189 (lire en ligne, consulté le 15 décembre 2020).

Bibliographie

Articles

(en) Emmerich Wilhelm, « The Art and Science of Solubility Measurements : What Do We Learn? », Netsu Sokutei, vol. 39, n^o 2,‎ 2012, p. 61-86 (lire en ligne [PDF]).
(en) Emmerich Wilhelm, « Solubilities, Fugacities and All That in Solution Chemistry », Journal of Solution Chemistry, vol. 44,‎ 23 janvier 2015, p. 1004-1061 (DOI 10.1007/s10953-014-0279-8).
(en) H. C. Van Ness et M. M. Abbott, « Vapor‐liquid equilibrium. : Part VI. Standard state fugacities for supercritical components. », AIChE J., vol. 25, n^o 4,‎ juillet 1979, p. 645-653 (lire en ligne).

Ouvrages

Christophe Coquelet et Dominique Richon, Propriétés thermodynamiques : Détermination pour les mélanges, vol. BE 8 031, Techniques de l'ingénieur, 2007, 12 p. (lire en ligne), p. 6.
Jean-Pierre Corriou, Thermodynamique chimique : Équilibres thermodynamiques, vol. J 1 028, Techniques de l'ingénieur, 1985, 31 p. (lire en ligne), p. 4-5.
Jean Vidal, Thermodynamique : Application au génie chimique et à l'industrie pétrolière, Paris, Éditions Technip, coll. « Publications de l'Institut français du pétrole. », 1997, 500 p. (ISBN 978-2-7108-0715-5, OCLC 300489419, lire en ligne), p. 168-169;209-210;295.
(en) J. P. O'Connell et J. M. Haile, Thermodynamics : Fundamentals for Applications, Cambridge University Press, 2005 (ISBN 978-1-139-44317-3, lire en ligne), p. 433-440.
(en) Ismail Tosun, The Thermodynamics of Phase and Reaction Equilibria, Newnes, 2012, 744 p. (ISBN 978-0-444-59502-7, lire en ligne), p. 448-466.
(en) Thomas B. Drew, Giles R. Cokelet, John W. Hoopes et Theodore Vermeulen, Advances in Chemical Engineering, vol. 7, Academic Press, 1968, 412 p. (ISBN 978-0-08-056554-5, lire en ligne), p. 166-170.
(en) John M. Prausnitz, Rudiger N. Lichtenthaler et Edmundo Gomes de Azevedo, Molecular Thermodynamics of Fluid Phase Equilibria, Upper Saddle River, N.J., Prentice Hall, 1999, 3^e éd. (1^re éd. 1967), 860 p. (ISBN 978-0-13-977745-5, OCLC 40607566, lire en ligne), p. 586-596.

Énoncé, définitions et démonstration

Énoncé de la loi de Henry

Constante de Henry

Définition thermodynamique

Dépendance à la pression

Dépendance à la température

Calcul théorique par une équation d'état

Formes usuelles

Démonstration de la loi de Henry

Limites et extensions de la loi de Henry

Limites de la loi idéale

Conditions de pression

Composition de la phase liquide

Cas des solvants, loi de Raoult

Extensions aux mélanges réels

Mélanges binaires

Lois des équilibres binaires

Lois des équilibres binaires idéaux

Équations de Krichevsky-Kasarnovsky et Krichevsky-Ilinskaya

Mélanges multicomposants

Lois des équilibres multicomposants

Lois des équilibres multicomposants idéaux

Application à un mélange ternaire : un soluté et deux solvants

Applications

Étude de la solubilité

En fonction de la pression

En fonction de la température

Pressurisation des boissons gazeuses

Solubilité des gaz atmosphériques dans le sang

Constantes de Henry pour des gaz dissouts dans l'eau

Notations

Notes et références

Notes

Bibliographie

Articles connexes