Longueur d'onde

L’axe x représente les distances parcourues, et y est la valeur à un instant donné d’une grandeur qui varie (par exemple la pression de l’air pour une onde sonore ou l’amplitude du champ électrique ou magnétique d’une onde lumineuse).

Données clés

Unités SI	m
Dimension	L
Base SI	m
Nature	Grandeur vectorielle extensive
Symbole usuel	${\displaystyle \lambda }$
Lien à d'autres grandeurs	${\displaystyle \lambda _{0}={\frac {c}{f}}}$ ${\displaystyle \lambda =T.c}$

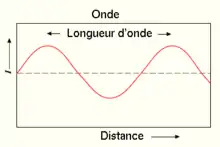
La longueur d’onde est une grandeur physique caractéristique d'une onde monochromatique dans un milieu homogène, définie comme la distance séparant deux maxima consécutifs de l'amplitude^[1].

La longueur d'onde dépend de la célérité ou vitesse de propagation de l'onde dans le milieu qu'elle traverse. Lorsque l'onde passe d'un milieu à un autre, dans lequel sa célérité est différente, sa fréquence reste inchangée, mais sa longueur d'onde varie (Dic. Phys.).

Lorsque l'onde n'est pas monochromatique, l'analyse harmonique permet de la décomposer en une somme d'ondes monochromatiques. Les phénomènes physiques ne sont jamais strictement périodiques ; l'analyse spectrale aboutit à une somme infinie d'ondes monochromatiques. On considère alors la longueur d'onde dominante, c'est-à-dire celle qui correspond à la fréquence qui transporte le plus d'énergie, ou à la fréquence centrale de la plage qui transporte le plus d'énergie.

Les longueurs d'onde sont d'un usage courant dans tous les domaines où des longueurs sont pertinentes : cavités résonantes en acoustique, antennes en radio, interférences en optique et dans les techniques dérivées de l'optique, radars, échographie, médecine nucléaire, radiologie médicale, lasers.

Généralités

Représentation de la longueur d’onde d’une fonction sinus.

Une onde est une perturbation qui se propage dans un milieu sans modifier de façon permanente ses propriétés.

Pour étudier ces perturbations, il est utile de simplifier la réalité, en considérant que le milieu est homogène et que les ondes sont monochromatiques, c'est-à-dire se répètent à l'infini avec une seule fréquence. L'analyse spectrale montre que, si les relations physiques dans le milieu sont linéaires, toutes les perturbations peuvent se décrire en une série, éventuellement infinie, de phénomènes périodiques monochromatiques, décrits par des sinusoïdes. On étudie séparément les transitions entre les milieux homogènes. Si un milieu varie progressivement, on considère que cette variation est une suite de transitions entre des milieux extrêmement proches.

Dans ces conditions et avec ces méthodes, l'étude des ondes monochromatiques dans un milieu homogène est la base de toutes les autres études.

Dans un milieu homogène, une perturbation monochromatique se propage avec une célérité constante. Si on observe l'état du milieu en un point donné, il se retrouve identiquement à chaque période. Si on observe l'état du milieu entier en un instant donné, la longueur l'onde est la distance entre deux points qui sont au même état^[2]. On peut choisir comme point de référence pour la mesure le passage en baisse au point d'équilibre, ou tout autre point bien défini.

En physique, on note souvent la longueur d'onde par la lettre grecque λ (lambda).

Si l'onde décrit une fonction périodique quelconque, on peut définir la longueur d’onde comme le plus petit λ > 0 tel que pour tout x, on ait :

${\displaystyle \displaystyle {f(x+\lambda )=f(x)}}$

La longueur d’onde est l’équivalent spatial de la période temporelle. En effet, la longueur d’onde est la distance parcourue par l’onde au cours d’une période. Si on appelle c la célérité de l’onde et T sa période temporelle et f sa fréquence, on a :

${\displaystyle \lambda =c*T}$ ce qui équivaut à ${\displaystyle \lambda ={\frac {c}{f}}}$ puisque ${\displaystyle T={\frac {1}{f}}}$

La période est l’équivalent temporel de la longueur d’onde : la période est le temps minimal qui s’écoule entre deux répétitions identiques de l’onde en un même point. Pour une onde sinusoïdale, la longueur d’onde est la distance entre deux pics de même signe successifs.

La longueur d'onde en optique

Le spectre de la lumière visible avec les raies de Fraunhofer.

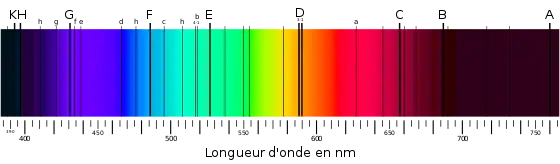
La longueur d'onde a une importance historique et pratique en optique. Au XIX^e siècle, Joseph von Fraunhofer étudiait le spectre solaire, et relia les couleurs de la lumière décomposée par le prisme optique aux longueurs d'onde des rayonnements correspondants, calculées d'après les interférences au passage d'un réseau optique. Les réseaux optiques relient, par une relation géométrique, les longueurs d'onde aux couleurs. Les réseaux optiques et les filtres interférentiels continuent d'avoir beaucoup d'applications, et leur calcul implique la longueur d'onde. On a donc l'habitude, en optique, de caractériser les rayonnements par leur longueur d'onde.

Quand on parle de longueur d'onde en optique sans autre précision, il faut comprendre longueur d'onde dans le vide.

La vitesse de la lumière dans l'air est peu différente de celle dans le vide, mais elle varie sensiblement dans les divers milieux qu'elle traverse, l'eau, les verres optiques, les milieux organiques qui composent l'œil humain. La fréquence, liée à l'énergie que transporte le rayonnement électromagnétique quand on le considère comme un flux de photons, est invariable. Par conséquent, la longueur d'onde varie selon les milieux traversés.

La variation de vitesse provoque, au passage d'un milieu à un autre, des réfractions. Quand la célérité de la lumière varie, la longueur d'onde varie. Cette variation dépend légèrement de la fréquence, ce qui cause aussi de la dispersion.

La longueur d'onde dans le matériau de la fibre optique est un paramètre capital pour en déterminer le mode de transmission.

Onde électromagnétique

Une onde électromagnétique se propage dans le vide, à une vitesse constante et indépassable. La vitesse de la lumière dans le vide c est une importante constante physique.

${\displaystyle \lambda _{0}={\frac {c}{\nu }}}$

où :

• ${\displaystyle \lambda _{0}}$ est la longueur d’onde dans le vide de l’onde ; unité = mètre (m)
• c est la vitesse de la lumière (≈3 × 10⁸ m/s) ; unité = mètre par seconde (m/s)
• ${\displaystyle \nu }$ (nu) est la fréquence de l’onde ; unité = hertz (Hz)

Pour des raisons pratiques, on répartit les rayonnements électromagnétiques en classes de fréquence, et par conséquent de longueur d'onde, dont les limites peuvent varier quelque peu selon les auteurs.

Longueur d'onde de De Broglie

Louis de Broglie a découvert que toutes les particules physiques dotées d’une quantité de mouvement ont une longueur d’onde, nommée longueur d’onde de De Broglie (voir l’article Mécanique ondulatoire). Pour une particule relativiste, la longueur d’onde de De Broglie est donnée par

${\displaystyle \lambda ={\frac {h}{p}}={\frac {h}{mv}}={\frac {h}{\gamma m_{0}v}}={\frac {h}{m_{0}v}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

Où: ${\displaystyle ~h~}$ est la constante de Planck, ${\displaystyle ~p~}$ est la quantité de mouvement de la particule, ${\displaystyle ~\gamma ~}$ le facteur de Lorentz, ${\displaystyle ~m_{0}~}$ la masse de la particule au repos, ${\displaystyle ~v~}$ la vitesse, et ${\displaystyle ~c~}$ la célérité de la lumière dans le vide.

Annexes

Notes et références