Théorie élémentaire des nombres

Le terme élémentaire désigne généralement une méthode qui n'use pas d'analyse complexe. Par exemple, le théorème des nombres premiers a été prouvé en utilisant une analyse complexe en 1896, mais la preuve élémentaire n'a été trouvée qu'en 1949 par Erdős et Selberg. Le terme est quelque peu ambigu : par exemple, les preuves basées sur des théorèmes taubériens complexes (par exemple le théorème de Wiener-Ikehara) sont souvent considérées comme très éclairantes mais non élémentaires. Une preuve élémentaire peut être plus longue et plus difficile pour la plupart des lecteurs qu'une preuve non élémentaire.

La théorie des nombres a la réputation d'être un domaine dont beaucoup de résultats peuvent être compris par le profane. En même temps, les preuves de ces résultats ne sont pas particulièrement accessibles, en partie parce que la gamme d'outils qu'ils utilisent est exceptionnellement large en mathématiques^[2].

Beaucoup de questions en théorie élémentaire des nombres apparaissent simples mais requièrent de très profondes considérations et de nouvelles approches, tels les exemples suivants :

• La conjecture de Goldbach concernant l'expression des nombres pairs comme somme de deux nombres premiers,
• La conjecture des nombres premiers jumeaux à propos de l'infinité des paires de nombres premiers consécutifs, et
• La conjecture de Syracuse concernant une simple itération.

La théorie des équations diophantiennes a même été montrée comme étant indécidable, c’est-à-dire qu’on peut construire une équation explicite dont l’existence de solutions ne peut être démontrée à l’aide des axiomes usuels des mathématiques (c’est le théorème de Matiyasevich).

Théorie analytique des nombres

La fonction zêta de Riemann ζ(s) dans le plan complexe. La couleur d'un point s code la valeur de ζ(s): les couleurs proches du noir indiquent des valeurs proches de zéro, alors que la teinte code l'argument de la valeur.

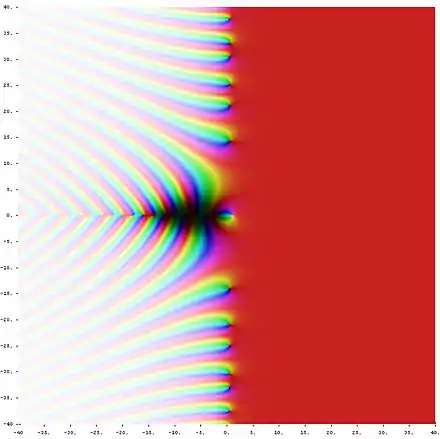
La théorie analytique des nombres peut être définie :

• par rapport à ses outils, c'est-à-dire l'étude des entiers au moyen d'outils d'analyse réelle et complexe^[3] ;
• par rapport à ses intérêts, c'est-à-dire l'étude des estimations sur la taille et la densité, par opposition aux identités^[4].

Certains sujets généralement considérés comme faisant partie de la théorie analytique des nombres, par exemple la théorie des cribles, sont définis plutôt par la seconde définition.

L'action du groupe modulaire sur le plan. La région en gris est le domaine fondamental standard.

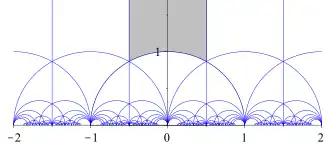
Voici des exemples de problèmes en théorie analytique des nombres : le théorème des nombres premiers, la conjecture de Goldbach (ou la conjecture des nombres premiers jumeaux ou les conjectures de Hardy-Littlewood), le problème de Waring ou encore l'hypothèse de Riemann^[5]. Certains des outils les plus importants de la théorie analytique des nombres sont la méthode du cercle, les méthodes des cribles et les fonctions L. La théorie des formes modulaires (et plus généralement des formes automorphes) occupe également une place de plus en plus centrale en théorie analytique des nombres^[6].

Théorie algébrique des nombres

Un nombre algébrique est un nombre complexe qui est solution d'une équation polynomiale à coefficients dans le corps ${\displaystyle \mathbb {Q} }$. Par exemple, toute solution ${\displaystyle x}$ de ${\displaystyle x^{5}+(11/2)x^{3}-7x^{2}+9=0}$ est un nombre algébrique. La théorie algébrique des nombres étudie les champs de nombres algébriques. Ainsi, les théories analytique et algébrique des nombres peuvent se chevaucher : la première est définie par ses méthodes, la seconde par ses objets d'étude.

Ernst Kummer

Les fondations de cette branche telle que nous la connaissons, ont été établies à la fin du XIX^e siècle, lorsque les idéaux et la valuation ont été développés. L'impulsion du développement des idéaux (par Ernst Kummer) semble provenir de l'étude des lois de réciprocité supérieure^[7], c'est-à-dire des généralisations de la loi de réciprocité quadratique.

Les corps sont souvent étudiés comme extensions d'autres corps plus petits: un corps L est dit être une extension d'un corps K si L contient K. La classification des extensions abéliennes a fait l'objet du programme de théorie des corps de classes, initié à la fin du XIX^e siècle (en partie par Kronecker et Eisenstein) et réalisé en grande partie en 1900-1950.

La théorie d'Iwasawa est un exemple de domaine de recherche actif en théorie algébrique des nombres. Le programme de Langlands, l'un des principaux programme de recherche actuels à grande échelle en mathématiques, est parfois décrit comme une tentative de généraliser la théorie des corps de classes aux extensions non abéliennes.

Géométrie diophantienne

Le problème central de la géométrie diophantienne est de déterminer quand une équation diophantienne a des solutions, et si oui, combien. L'approche adoptée est de considérer les solutions d'une équation comme un objet géométrique.

Par exemple, une équation à deux variables définit une courbe dans le plan. Plus généralement, une équation, ou un système d'équations, à deux ou plusieurs variables définit une courbe, une surface, etc., dans un espace à n dimensions. En géométrie diophantienne, on se demande s'il existe des points rationnels (points dont toutes les coordonnées sont rationnelles) ou des points entiers (points dont toutes les coordonnées sont des entiers) sur la courbe ou la surface. S'il y a de tels points, l'étape suivante consiste à demander combien il y en a et comment ils sont répartis. Une question fondamentale dans cette direction est la suivante : existe-t-il un nombre fini ou infini de points rationnels sur une courbe (ou surface) donnée ? Qu'en est-il des points entiers ?

Un exemple serait l'équation de Pythagore ${\displaystyle x^{2}+y^{2}=1}$ ; nous voudrions étudier ses solutions rationnelles, c'est-à-dire ses solutions ${\displaystyle (x,y)}$ telles que x et y soient tous deux rationnels. Cela revient à demander toutes les solutions entières de ${\displaystyle a^{2}+b^{2}=c^{2}}$ ; toute solution à cette dernière équation nous donne une solution ${\displaystyle x=a/c}$, ${\displaystyle y=b/c}$. Cela est équivalent au fait de demander tous les points à coordonnées rationnelles sur la courbe décrite par ${\displaystyle x^{2}+y^{2}=1}$ (cette courbe se trouve être le cercle unité).

Deux exemples de courbes elliptiques. Celles-ci peuvent être vues comme une tranche d'un tore en quatre dimensions.

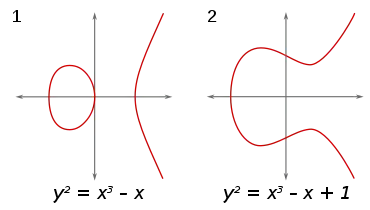
La reformulation des questions sur les équations en termes de points sur les courbes s'avère fructueuse. La finitude ou non du nombre de points rationnels ou entiers sur une courbe algébrique, s'avère dépendre de façon cruciale du genre de la courbe. Ce domaine est étroitement lié aux approximations diophantiennes : étant donné un nombre, à quel point peut-il être approché par des rationnels ? (On considère qu'un rationnel ${\displaystyle a/b}$, avec a et b premiers entre eux, est une bonne approximation de ${\displaystyle x}$ si ${\displaystyle |x-a/b|<{\frac {1}{b^{c}}}}$, où ${\displaystyle c}$ est grand.) Cette question est d'un intérêt particulier si ${\displaystyle x}$ est un nombre algébrique. Si ${\displaystyle x}$ ne peut pas être bien approximé, alors certaines équations n'ont pas de solutions entières ou rationnelles. De plus, plusieurs concepts s'avèrent cruciaux à la fois en géométrie diophantienne et dans l'étude des approximations diophantiennes. Cette question est également d'un intérêt particulier en théorie des nombres transcendants : si un nombre peut être mieux approché que n'importe quel nombre algébrique, alors c'est un nombre transcendant. C'est par cet argument qu'il a été démontré que ${\displaystyle \pi }$ et ${\displaystyle \mathrm {e} }$ sont transcendants.

La géométrie diophantienne ne doit pas être confondue avec la géométrie des nombres, qui est une collection de méthodes graphiques pour répondre à certaines questions de la théorie algébrique des nombres. Le terme de géométrie arithmétique est sans doute le plus souvent utilisé lorsque l'on veut mettre l'accent sur les liens avec la géométrie algébrique moderne (comme le théorème de Faltings) plutôt que sur les techniques des approximations diophantiennes.

Théorie probabiliste des nombres

En prenant un nombre au hasard entre un et un million, quelle est la probabilité qu'il soit premier ? C'est juste une autre façon de demander combien il y a de nombres premiers entre un et un million. Et combien de diviseurs aura-t-il, en moyenne ?

Une grande partie de la théorie probabiliste des nombres peut être considérée comme une branche de l'étude de variables qui sont presque indépendantes les unes des autres. Parfois, une approche probabiliste non rigoureuse conduit à un certain nombre d'algorithmes heuristiques et de problèmes ouverts, notamment la conjecture de Cramér.

Théorie combinatoire des nombres

Soit A un ensemble de N entiers. Considérons l'ensemble A + A = { m + n | m, n ∈ A } constitué de toutes les sommes de deux éléments de A. A + A est-il beaucoup plus grand que A? À peine plus grand ? A ressemble-t-il à une suite arithmétique? Si nous partons d'un ensemble infini A assez grand, contient-il beaucoup d'éléments dans la progression arithmétique ${\displaystyle a+b,a+2b,a+3b,\ldots ,a+nb}$ ?

Ces questions sont caractéristiques de la théorie combinatoire des nombres. Son intérêt pour les questions de croissance et de distribution tient en partie au développement de ses liens avec la théorie ergodique, la théorie des groupes finis, la théorie des modèles et d'autres domaines. Les ensembles étudiés n'ont pas besoin d'être des ensembles d'entiers, mais plutôt des sous-ensembles de groupes non commutatifs, pour lesquels le symbole de multiplication, et non le symbole d'addition, est traditionnellement utilisé; ils peuvent également être des sous-ensembles d'anneaux.

Théorie algorithmique des nombres

Il y a deux questions principales: « pouvons-nous calculer cela ? » et « pouvons-nous le calculer rapidement ? ». N'importe qui peut tester si un nombre est premier ou, si ce n'est pas le cas, obtenir sa décomposition en facteurs premiers ; le faire rapidement devient plus compliqué. Nous connaissons aujourd'hui des algorithmes rapides pour tester la primalité, mais, malgré beaucoup de travail (à la fois théorique et pratique), aucun algorithme n'est vraiment rapide pour cette tâche.

La difficulté d'un calcul peut être utile : les protocoles modernes de chiffrement de messages (par exemple, le RSA) dépendent de fonctions connues de tous, mais dont les inverses ne sont connus que d'un petit nombre, et les trouver par ses propres moyens prendrait trop de temps. Alors que de nombreux problèmes de calcul en dehors de la théorie des nombres sont connus, la plupart des protocoles de chiffrement actuels sont basés sur la difficulté de quelques problèmes théoriques.

Il s'avère que certaines choses peuvent ne pas être calculables du tout ; cela peut être prouvé dans certains cas. Par exemple, en 1970, il a été prouvé, résolvant ainsi le dixième problème de Hilbert, qu'il n'existe pas de machine de Turing capable de résoudre toutes les équations diophantiennes^[8]. Cela signifie que, compte tenu d'un ensemble d'axiomes calculables et énumérables, il existe des équations diophantiennes pour lesquelles il n'existe aucune démonstration, à partir des axiomes, de savoir si l'ensemble des équations a ou non des solutions entières.

Origines

Aube de l'arithmétique

La tablette Plimpton 322.

La découverte historique d'une nature arithmétique est un fragment de tableau : la tablette d'argile brisée Plimpton 322 (Larsa, Mésopotamie, vers 1800 avant notre ère) contient une liste « triplets pythagoriciens », c'est-à-dire des entiers tels que ${\displaystyle a^{2}+b^{2}=c^{2}}$^[9]. Ceux-ci sont trop grands pour avoir été obtenus par recherche exhaustive^[10]. La disposition de la tablette suggère^[11] qu'elle a été construite au moyen de ce qui équivaut, dans un langage moderne, à l'identité^[12]

${\displaystyle \left({\frac {1}{2}}\left(x-{\frac {1}{x}}\right)\right)^{2}+1=\left({\frac {1}{2}}\left(x+{\frac {1}{x}}\right)\right)^{2}}$.

Alors que la théorie des nombres babylonienne consiste en ce seul fragment, l'algèbre babylonienne (au sens de l'« algèbre » des études secondaires) était exceptionnellement bien développée^[13]. Pythagore aurait appris les mathématiques auprès des Babyloniens^[14]. Beaucoup de sources antérieures^[15] déclarent que Thalès et Pythagore ont voyagé et étudié en Égypte.

La découverte de l'irrationalité de √2 est attribuée aux premiers pythagoriciens^{[16],[17],[18]}. Cette découverte semble avoir provoqué la première crise de l'histoire mathématique ; sa preuve et sa diffusion sont parfois attribuées à Hippase, qui a été expulsé de la secte pythagoricienne^[19]. Cela a forcé à faire une distinction entre les nombres (entiers et rationnels), d'une part, et les longueurs et les proportions (nombres réels), d'autre part^[20].

Le théorème des restes chinois apparaît comme un exercice dans le traité Sunzi Suanjing (III^e, IV^e, ou V^e siècle av. J.-C.)^[21],[22].

Diophante

Page de couverture de l'édition de 1621 de l'Arithmetica de Diophante, traduite en latin par Claude Gaspard Bachet de Méziriac.

Nous ne savons que très peu de choses sur Diophante d'Alexandrie ; il a probablement vécu au troisième siècle de notre ère, c'est-à-dire environ cinq cents ans après Euclide. L'Arithmetica est une collection de problèmes où la tâche est de trouver des solutions rationnelles à des équations polynomiales, généralement de la forme ou ${\displaystyle f(x,y)=z^{2}}$ ou ${\displaystyle f(x,y,z)=w^{2}}$. Ainsi, de nos jours, on parle d'équations diophantiennes quand on parle d'équations polynomiales dont on doit trouver des solutions rationnelles ou entières.

Tandis que Diophante s'intéressait surtout aux solutions rationnelles, il émettait des conjectures sur les entiers naturels, comme le fait que tout entier est la somme de quatre carrés.

Arithmétique à l'âge d'or islamique

Johannes Hevelius, Selenographia (Gdansk, 1647). Représentations d'Alhasen, Ibn al-Haytham, à gauche, tenant un diagramme géométrique symbolisant la connaissance par la raison et Galilée à droite, tenant un télescope et symbolisant la connaissance par les sens.

Au début du IX^e siècle, le calife Al-Ma'mūn ordonna la traduction de nombreuses œuvres mathématiques grecques et d'au moins une œuvre sanscrite (le Sindhind, qui pourrait^[32] ou non^[33] être le Brāhmasphuṭasiddhānta de Brahmagupta). L'œuvre principale de Diophante, l'Arithmetica, a été traduite en arabe par Qusta ibn Luqa (820-912). Selon Roshdi Rashed^[34], Alhazen, contemporain d'Al-Karaji, connaissait ce qui sera plus tard appelé le théorème de Wilson.

Théorie des nombres moderne

Fermat

Pierre de Fermat.

Pierre de Fermat (1601-1665) n'a jamais publié ses écrits ; en particulier, son travail sur la théorie des nombres est contenu presque entièrement dans des lettres aux mathématiciens et dans les notes et marges privées^[35]. Il n'a presque écrit aucune démonstration en théorie des nombres. Il n'avait aucun modèle dans le domaine^[36]. Il a fait un usage répété du raisonnement par récurrence, en introduisant la méthode de descente infinie. Un des premiers intérêts de Fermat était les nombres parfaits (qui apparaissent dans les Éléments IX d'Euclide) et les nombres amicaux ; ceci l'amène à travailler sur des diviseurs entiers, qui furent dès le début parmi les sujets de la correspondance (année 1636 et suivantes) qui le mettent en contact avec la communauté mathématique de l'époque^[37]. Il avait déjà étudié attentivement l'édition de Bachet de Diophante^[38] ; après 1643, ses intérêts se sont portés vers les problèmes diophantiens et somme de carrés^[39] (aussi traités par Diophante).

Les résultats de Fermat en arithmétique incluent :

• Le petit théorème de Fermat (1640)^[40], indiquant que, si a n'est pas divisible par un nombre premier p, alors ${\displaystyle a^{p-1}\equiv 1{\bmod {p}}}$.
• Si a et b ne sont pas premiers entre eux, ${\displaystyle a^{2}+b^{2}}$ n'est pas divisible par n'importe quel nombre premier congru à −1 modulo 4^[41] et tout nombre premier congru à 1 modulo 4 peut être écrit sous la forme ${\displaystyle a^{2}+b^{2}}$^[42]. Ces deux énoncé datent de 1640 ; en 1659, Fermat écrivit à Huygens qu'il avait prouvé la dernière déclaration par descente infinie^[43]. Fermat et Frenicle ont fait quelques travaux (certains erronés) sur d'autres formes quadratiques^[44].
• Fermat a posé le problème de la résolution de ${\displaystyle x^{2}-Ny^{2}=1}$ comme un défi pour les mathématiciens anglais (1657). Le problème a été résolu en quelques mois par Wallis et Brouncker^[45]. Fermat a considéré leur solution valide, mais a souligné qu'ils avaient fourni un algorithme sans preuve (comme Jayadeva et Bhaskara, bien que Fermat ne le saurait jamais). Il déclare qu'une preuve peut être trouvée par descente infinie.
• Fermat déclare et prouve (par descente infinie) en appendice aux observations sur Diophante (Obs XLV) que l'équation diophantienne ${\displaystyle x^{4}+y^{4}=z^{4}}$ n'a pas de solutions non triviales dans les entiers^[46]. Fermat a également mentionné à ses correspondants qu'il n'y a pas de solutions non triviales à ${\displaystyle x^{3}+y^{3}=z^{3}}$, et que cela pourrait être prouvé par descente infinie^[47]. La première preuve connue est due à Euler (1753, par descente infinie)^[48].

La déclaration de Fermat (« dernier théorème de Fermat ») d'avoir montré qu'il n'y a pas de solutions à l'équation ${\displaystyle x^{n}+y^{n}=z^{n}}$ pour tout ${\displaystyle n\geq 3}$ apparaît seulement en marge d'une copie d'Arithmetica de Diophante.

Euler

Leonhard Euler.

L'intérêt de Leonhard Euler (1707-1783) pour la théorie des nombres fut d'abord stimulé en 1729, quand un de ses amis, l'amateur Goldbach, l'orienta vers une partie du travail de Fermat sur le sujet^[49],[50]. Cela a été appelé la « renaissance » de la théorie moderne des nombres^[38], après le relatif manque de succès de Fermat pour attirer l'attention de ses contemporains sur le sujet^[51]. Le travail d'Euler sur la théorie des nombres comprend les éléments suivants^[52] :

• Preuves des déclarations de Fermat. Cela inclut le petit théorème de Fermat (généralisé par Euler aux modules non premiers) ; le fait que ${\displaystyle p=x^{2}+y^{2}}$ si et seulement si ${\displaystyle p\equiv 1{\bmod {4}}}$ ; un travail en vue d'une preuve du théorème des quatre carrés (la première preuve complète est de Joseph-Louis Lagrange (1770), ensuite améliorée par Euler lui-même^[53]) ; l'absence de solutions entières non nulles à ${\displaystyle x^{4}+y^{4}=z^{2}}$ (impliquant le cas n = 4 du dernier théorème de Fermat, le cas n = 3 a aussi été traité par Euler).
• L'équation de Pell-Fermat^[54], et de son lien aux fractions continues^[55].
• Premiers pas vers la théorie analytique des nombres. Dans son travail de sommes de quatre carrés, de partitions, de nombres pentagonaux et de la distribution des nombres premiers, Euler fut le pionnier de l'utilisation de ce qui peut être vu comme une analyse (en particulier, des séries infinies) en théorie des nombres. Il a effectué un travail précoce remarquable (mais non entièrement rigoureux) sur ce que l'on appellera plus tard la fonction zêta de Riemann^[56].
• Formes quadratiques. À la suite de Fermat, Euler a poursuivi ses recherches sur la question de savoir quels nombres premiers pouvaient être exprimés sous la forme ${\displaystyle x^{2}+Ny^{2}}$, préfigurant alors la loi de réciprocité quadratique^{[57],[58],[59]}.
• Équations diophantiennes. Euler a travaillé sur quelques équations diophantiennes^[60],[61]. En particulier, il a étudié le travail de Diophante, et a essayé de le systématiser, mais le temps n'était pas encore mûr pour un tel effort — la géométrie algébrique était encore à ses balbutiements^[62]. Il remarqua un lien entre les problèmes diophantiens et les intégrales elliptiques, dont il avait lui-même initié l'étude^[62].

Lagrange, Legendre, et Gauss

Disquisitiones Arithmeticae de Carl Friedrich Gauss, première édition.

Joseph-Louis Lagrange (1736-1813) fut le premier à donner des preuves complètes à certains travaux et observations de Fermat et Euler – par exemple, le théorème des quatre carrés et la théorie de l'équation de Pell-Fermat. Il a également étudié les formes quadratiques définissant leur relation d'équivalence, montrant comment les mettre sous forme réduite, etc.

Adrien-Marie Legendre (1752-1833) fut le premier à énoncer la loi de réciprocité quadratique. Il a également conjecturé ce qui équivaut aujourd'hui au théorème des nombres premiers et au théorème de Dirichlet sur les progressions arithmétiques. Il a donné une analyse complète de l'équation ${\displaystyle ax^{2}+by^{2}+cz^{2}=0}$^[63]. Durant la fin de sa vie, il fut le premier à prouver le dernier théorème de Fermat pour n = 5^[64].

Carl Friedrich Gauss.

Dans ses Disquisitiones Arithmeticae (1798), Carl Friedrich Gauss (1777-1855) a démontré la loi de réciprocité quadratique et développé la théorie des formes quadratiques. Il a également introduit la notation de congruence et a consacré une section aux tests de primalité^[65]. La dernière section des Disquisitiones établit un lien entre les racines de l'unité et la théorie des nombres^[66]. De cette façon, Gauss a sans doute amorcé le travail d'Évariste Galois et de la théorie algébrique des nombres.

Division en sous-domaines

Peter Gustav Lejeune Dirichlet.

Commençant au début du XIX^e siècle, les développements suivants ont progressivement eu lieu :

• L'émergence de la théorie des nombres comme domaine d'étude^[67].
• Le développement d'une grande partie des mathématiques modernes nécessaires à la théorie moderne des nombres : analyse complexe, théorie des groupes, théorie de Galois — accompagné d'une plus grande rigueur d'analyse et d'abstraction dans l'algèbre.
• La subdivision primitive de la théorie des nombres en ses sous-domaines modernes, en particulier la théorie analytique et algébrique des nombres. La théorie algébrique des nombres émerge avec l'étude de la réciprocité et de la cyclotomie, mais celle-ci a véritablement pris son essor avec le développement de l'algèbre abstraite et de la théorie de la valuation. Un point de départ de la théorie analytique des nombres est le théorème de Dirichlet sur les progressions arithmétiques (1837)^[3],[68], dont la preuve introduisait les fonctions L et impliquait une analyse asymptotique^[69]. La première utilisation des idées analytiques en théorie des nombres revient à Euler (1730)^[70],[71] avec l'utilisation de séries et de limites. L'utilisation de l'analyse complexe en théorie des nombres vient plus tard : le travail de Bernhard Riemann (1859) sur la fonction zêta est le point de départ^[72]. Le théorème des quatre carrés de Jacobi (1839) a pris un rôle de premier plan en théorie analytique des nombres (formes modulaires)^[73].

Bibliographie

Ouvrages cités

• (en) Tom M. Apostol, Introduction to Analytic Number Theory, Springer, coll. « Undergraduate Texts in Mathematics », 1976, 340 p. (ISBN 978-0-387-90163-3, lire en ligne)
• (de) Oskar Becker, « Die Lehre von Geraden und Ungeraden im neunten Buch der euklidischen Elemente », Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, vol. 3,‎ 1936, p. 533-553
• (en) Carl Benjamin Boyer et Uta C. Merzbach, A History of Mathematics, New York, Wiley, 1991, 2^e éd. (1^re éd. 1968), 736 p. (ISBN 978-0-471-54397-8), édition 1968 sur archive.org
• (en) Aryabhata et Walter Eugene Clark (traducteur), The Āryabhaṭīya of Āryabhaṭa : An ancient Indian work on Mathematics and Astronomy, University of Chicago Press, 1930 (lire en ligne)
• (en) Henry Thomas Colebrooke, Algebra, with Arithmetic and Mensuration, from the Sanscrit of Brahmegupta and Bháscara, Londres, J. Murray, 1817 (lire en ligne)
• (en) Harold Davenport et Hugh L. Montgomery, Multiplicative Number Theory, Springer, coll. « GTM » (n^o 74), 2000, 3 (révisée) éd. (ISBN 978-0-387-95097-6)
• (en) Harold M. Edwards, « Euler and Quadratic Reciprocity », Mathematics Magazine, vol. 56, n^o 5,‎ 1983, p. 285-291 (JSTOR 2690368)
• (en) Harold M. Edwards, Fermat's Last Theorem: a Genetic Introduction to Algebraic Number Theory, Springer Verlag, coll. « GTM » (n^o 50), 2000, réimpression de l'édition de 1977 éd. (1^re éd. 1977) (ISBN 978-0-387-95002-0, lire en ligne)
• (fr + la) Pierre de Fermat, Varia Opera Mathematica, Toulouse, Joannis Pech, 1679 (lire en ligne)
• (en) Kurt von Fritz, « The Discovery of Incommensurability by Hippasus of Metapontum », dans J. Christianidis, Classics in the History of Greek Mathematics, Berlin, Kluwer (Springer), 2004 (ISBN 978-1-4020-0081-2)
• (en) Catherine Goldstein et Norbert Schappacher, « A book in search of a discipline », dans C. Goldstein, N. Schappacher et Joachim Schwermer, The Shaping of Arithmetic after C. F. Gauss's "Disquisitiones Arithmeticae", Berlin & Heidelberg, Springer, 2007 (ISBN 978-3-540-20441-1, lire en ligne), p. 3-66
• (en) Andrew Granville, « Analytic number theory », dans Timothy Gowers, June Barrow-Green et Imre Leader, The Princeton Companion to Mathematics, Princeton University Press, 2008 (ISBN 978-0-691-11880-2, lire en ligne)
• (en) Thomas L. Heath, A History of Greek Mathematics, vol. 1 : From Thales to Euclid, Oxford, Clarendon Press, 1921 (lire en ligne)
• (en) Henryk Iwaniec et Emmanuel Kowalski, Analytic Number Theory, vol. 53, Providence, RI, AMS, coll. « AMS Colloquium Publications », 2004 (ISBN 0-8218-3633-1)
• (en) Lay Yong Lam et Tian Se Ang, Fleeting Footsteps: Tracing the Conception of Arithmetic and Algebra in Ancient China, Singapore, World Scientific, 2004 (ISBN 978-981-238-696-0, lire en ligne)
• (en) M. S. Mahoney, The Mathematical Career of Pierre de Fermat, 1601–1665, Princeton University Press, 1994, 2^e éd. (ISBN 978-0-691-03666-3, lire en ligne)
• (en) Proclus et Glenn Raymond Morrow (éditeur et traducteur), A Commentary on Book 1 of Euclid's Elements, Princeton University Press, 1992 (ISBN 978-0-691-02090-7, lire en ligne)
• (en) David Mumford, « Mathematics in India: reviewed by David Mumford », Notices of the American Mathematical Society, vol. 57, n^o 3,‎ 2010, p. 385-390 (lire en ligne)
• (en) Otto E. Neugebauer, The Exact Sciences in Antiquity, New York, Dover Publications, 1969, réimpression corrigée de l'édition de 1957 éd., 240 p. (ISBN 978-0-486-22332-2, lire en ligne)
• (en) Otto E. Neugebauer, Abraham Sachs et Albrecht Götze, Mathematical Cuneiform Texts, American Oriental Society etc., coll. « American Oriental Series » (n^o 29), 1945
• (en) Patricia O'Grady, « Thales of Miletus », The Internet Encyclopaedia of Philosophy, septembre 2004 (consulté le 7 février 2012)
• (en) Kim Plofker, Mathematics in India, Princeton (N.J.), Princeton University Press, 2008, 357 p. (ISBN 978-0-691-12067-6, lire en ligne). 
• (zh) Baocong Qian (dir.), Suanjing shi shu (Ten Mathematical Classics), Pékin, Zhonghua shuju, 1963 (lire en ligne)
• Roshdi Rashed, « Ibn al-Haytham et le théorème de Wilson », Archive for History of Exact Sciences, vol. 22, n^o 4,‎ 1980, p. 305-321 (DOI 10.1007/BF00717654)
• (en) Eleanor Robson, « Neither Sherlock Holmes nor Babylon: a Reassessment of Plimpton 322 », Historia Mathematica, vol. 28, n^o 28,‎ 2001, p. 167-206 (DOI 10.1006/hmat.2001.2317, lire en ligne [archive du 21 octobre 2014])
• (en) D. E. Smith, History of Mathematics, vol. I, New York, Dover Publications, 1958
• (fr + la) Paul Tannery, Charles Henry (éditeurs) et Pierre de Fermat, Œuvres de Fermat, Paris, Gauthier-Villars, 1891, 4 vol. (1912)
• (en) V. S. Varadarajan, Euler Through Time: A New Look at Old Themes, AMS, 2006 (ISBN 978-0-8218-3580-7, lire en ligne)
• (en) Bartel L. van der Waerden et Arnold Dresden (traducteur), Science Awakening, vol. 2, New York, Oxford University Press, 1961
• (en) André Weil, Number Theory : An approach through history from Hammurapi to Legendre [détail des éditions]

Autres ouvrages

• (en) Tom M. Apostol, An Introduction to the Theory of Numbers (MR 0568909)
• G. H. Hardy et E. M. Wright (trad. de l'anglais par François Sauvageot, préf. Catherine Goldstein), Introduction à la théorie des nombres [« An Introduction to the Theory of Numbers »] [détail de l’édition]
• (en) Hugh L. Montgomery et Robert C. Vaughan, Multiplicative Number Theory, vol. I : Classical Theory, Cambridge (GB), Cambridge University Press, 2007, 552 p. (ISBN 978-0-521-84903-6, lire en ligne)
• Jean-Pierre Serre, Cours d'arithmétique, 1970 [détail des éditions]
• (en) C. A. Truesdell, « Leonard Euler, Supreme Geometer », dans John Hewlett (trad.), Leonard Euler, Elements of Algebra, New York, Springer-Verlag, 1984, 5^e éd. (ISBN 978-0-387-96014-2, lire en ligne). La version en ligne ne contient pas l'introduction de Truesdell qui, quant à elle, est reproduite (légèrement abrégée) dans :
• (en) C. A. Truesdell, « Leonard Euler, Supreme Geometer », dans William Dunham, The Genius of Euler: reflections on his life and work, New York, MAA, coll. « MAA tercentenary Euler celebration » (n^o 2), 2007 (ISBN 978-0-88385-558-4, lire en ligne)

Articles connexes

• Liste des matières de la théorie des nombres
• Problème des bœufs d'Hélios

Liens externes

• Notices d'autorité :

  • BnF (données)
  • IdRef
  • LCCN
  • GND
  • Japon
  • Espagne
  • Israël
  • Tchéquie
• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Gran Enciclopèdia Catalana
  • Store norske leksikon
  • Universalis
• Initiation à la théorie des nombres
• Complément pédagogique depuis OpenClassRoom
• (en) J. S. Milne, « Algebraic Number Theory », 2014