

La rentrée atmosphérique est la phase durant laquelle un objet artificiel pénètre dans l'atmosphère d'un objet céleste et atteint des couches suffisamment denses pour provoquer des effets mécaniques et thermiques. L'objet en question peut être satellite, capsule spatiale ou fragment de fusée par exemple.
Les objets conçus par l'Homme
Le domaine est apparu dans les années 1950 aux États-Unis et en URSS, d'abord pour des objectifs stratégiques, concernant les missiles à longue portée disposant de véhicules de rentrée, puis pour un objectif politique : l'homme dans l'espace[1]. D'autres nations ont suivi et la connaissance du domaine est assez mondialement partagée sur le plan scientifique, même si peu de pays disposent aujourd'hui d'un lanceur capable de réaliser un vol humain : la Russie, la Chine et les États-Unis. L'Europe, le Japon et l'Inde ont cependant une capacité de lancement de satellites et sondes spatiales.
Les investissements consentis au démarrage de cette activité ont été considérables, en raison des moyens d'essais nécessaires. Ceci est moins vrai depuis les années 1970 et l'avènement des simulations numériques. Toutefois, ce domaine nécessite encore aujourd'hui une technologie coûteuse, même pour des sondes spatiales à objectif scientifique. Les moyens financiers sont l'apanage d'agences dédiées : National Aeronautics and Space Administration[2] (NASA), Agence spatiale fédérale russe[3] (Roscosmos), l'Agence d'exploration aérospatiale japonaise[4] (JAXA), l'Indian Space Research Organisation[5] (ISRO), l'Administration spatiale nationale chinoise[6] (CNSA), l'agence spatiale européenne[7] (ESA). En Europe, outre la France et le Royaume-Uni, qui disposaient déjà de connaissances liées aux programmes stratégiques, l'ESA a permis à l'Allemagne, l'Italie et d'autres pays européens d'acquérir une expertise dans le domaine.
Concernant les objets artificiels, on peut définir deux catégories suivant leurs performances aérodynamiques : les avions ou objets à grande latitude de manœuvre destinés à l'usage humain et les capsules habitables ou sondes spatiales à capacité de manœuvre faible ou nulle. Ces dernières ont des géométries extrêmement simples pour la section destinée à recevoir l'énergie cinétique provenant de la compression de l'air : sphère ou sphère-cône, avec ou non un tore de raccordement avec la partie arrière[8],[9].

Sonde Stardust sur son porteur. 
Ecorché de Stardust. 
Entrée de Stardust. 
Stardust de retour sur terre.
Trajectoire de rentrée
Les vitesses vont de quelques km/s à 47 km/s pour les objets d'origine humaine et peuvent dépasser 70 km/s pour les météores.
| Planète (date) | Masse (kg) | Vitesse (m/s) | Pente (degré) | |
|---|---|---|---|---|
| Apollo 4 | Terre (1967) | 5 425 | 11 140 | 7,07 |
| Stardust | Terre (2006) | 45,2 | 12 799 | 8,21 |
| Viking | Mars (1976) | 980 | 4 420 | 17 |
| Pathfinder | Mars (1997) | 584 | 7 620 | 14,06 |
| Pioneer 13 large probe | Vénus (1978) | 316,5 | 11 540 | 32,4 |
| Pioneer 13 north probe | Vénus (1978) | 91 | 11 670 | 68,7 |
| Galileo | Jupiter (1995) | 335 | 47 400 | 8,5 |
| Huygens | Titan (2006) | 319 | 6 100 | 65 |
| Météorite Tcheliabinsk | Terre (2013) | 1,2 × 107 | 19 020 | 18,2 |
Atmosphère et modèle gravitationnel
Les atmosphères sont caractérisées par leur composition et les variations avec l'altitude de la température et de la pression. Cette dernière valeur conditionne l'angle de rentrée afin de limiter l'échauffement du corps en restant dans une région peu dense. On peut décrire assez simplement le profil vertical de pression p ou de masse volumique en fonction de l'altitude h en supposant un milieu isotherme en équilibre hydrostatique décrit par l'équation
où g est l'accélération de la pesanteur. g=9.802 m/s2 sur terre, 3,711 m/s2 sur Mars. En remplaçant p par sa valeur issue de l'équation d'état dans laquelle est la constante universelle des gaz et la masse molaire moyenne, la résolution de l'équation d'équilibre de l'atmosphère donne ainsi un profil exponentiel
où pour la Terre est un paramètre permettant une bonne approximation dans la tranche d'altitude intéressante (valeur légèrement différente de la véritable valeur au sol), constitue le facteur d'échelle qui vaut environ 7,9 km pour la Terre, 11,1 km pour Mars, 5,3 km pour Vénus et 38 km pour Titan. Sur ce satellite de Saturne le faible gradient vertical permet donc d'utiliser pour l'entrée des trajectoires à plus grande pente par rapport au plan horizontal local.
La loi exponentielle implique qu'il n'existe pas de limite séparant l'atmosphère du vide spatial. On choisira donc une limite arbitraire à partir des effets sur l'objet, et tout d'abord sur son attitude, les effets sur la vitesse (mouvement du centre de gravité) étant légèrement postérieurs. Dans le cas terrestre on utilise généralement la valeur de 120 km. Cette valeur est arbitraire mais correcte pour la plupart des objets, qu'il s'agisse d'une sonde spatiale ou d'une navette spatiale. Elle est faible pour des objets de rapport diamètre/masse élevé comme les systèmes déployables.
Dans le cas général l'atmosphère utilisée pour prédire la rentrée est constituée par des profils verticaux de toutes les quantités d'intérêt (composition, température, pression, vents, etc.) dont il existe des bases de données comme le modèle GRAM (Global Reference Atmospheric Model) de la NASA[12] disponible pour toutes les atmosphères planétaires.
De la même façon on utilise des modèles géodétiques pour caractériser le profil de gravité. Le système standard est le WGS 84[13] (World Geodetic System), également utilisé par les systèmes GPS.
La trajectoire balistique
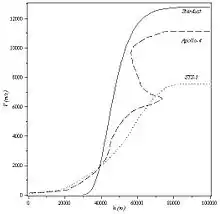
Dans le cas d'un corps dénué de portance l'objet est caractérisé par son coefficient balistique où m est la masse, Sref une surface de référence arbitraire et CA le coefficient de traînée relatif à cette surface (seul le produit SrefCA a une signification physique). On peut calculer assez facilement cette trajectoire si l'on suppose celle-ci rectiligne, de vitesse initiale V0, de pente avec un coefficient de traînée constant (trajectoire d'Allen). On en déduit l'accélération maximale
On remarque que l'accélération maximale est indépendante du coefficient balistique. On peut également calculer l'altitude à laquelle se produit cet évènement
où . À titre d'exemple dans le cas de Stardust β = 58 kg/m2[14] l'accélération maximale est de 615 m/s2 (environ 63 g), obtenue a 47,4 km d'altitude. Une telle valeur est trop faible pour influencer la conception mécanique de l'objet. Bien entendu ce paramètre est prépondérant pour la rentrée humaine qui doit être limitée à une valeur inférieure à 10 g.
La trajectoire d'un objet portant
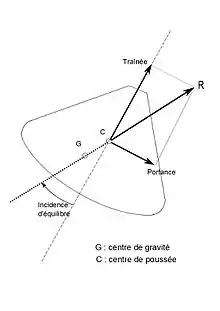
L'utilité d'utiliser des objets capables d'évoluer dans l'atmosphère s'est fait sentir très tôt. Cette technique[15] s'est manifestée d'abord modestement dans le programme Gemini puis beaucoup plus efficacement dans le programme Apollo. Ceci a évolué ultérieurement vers la conception d'un véritable avion : la navette spatiale.
La conception des capsules Gemini et Apollo est particulièrement intéressante du fait de sa simplicité. Ces engins sont de révolution (sauf quelques artefacts technologiques). La portance est obtenue grâce à un balourd statique, un déport du Centre des masses G de l'engin à l'écart de l'axe de symétrie (le Centre de portance C étant sur l'axe de symétrie). Cette portance est donc fixe en axes engin et pilotée par rotation de celui-ci par des jets de gaz. Ceci implique bien sûr l'existence de systèmes de guidage et de pilotage. L'incidence est donc également fixe : environ 30 degrés dans le cas d'Apollo, ce qui lui donne une portance définie par une finesse de 0.3 environ. Cette valeur, bien que très faible comparée à celle d'un avion, a cependant permis à Apollo 4 d'effectuer une ressource (au sens aéronautique). Ce principe a été utilisé plus récemment sur Mars Science Laboratory. Cette technique permet une meilleure précision d'atterrissage, environ 20 km contre plus d'une centaine dans le plan de la trajectoire pour un corps non piloté.
La séquence post-phase hypersonique
Lorsque la sonde a atteint Mach 1 à 1.5 (1.23 pour Stardust), un parachute supersonique est déployé. Il a pour fonction non seulement de ralentir la sonde mais également de la stabiliser durant la phase transsonique. Après passage en subsonique un parachute de grand diamètre prend le relais pour amener la vitesse à une valeur comprise entre 10 et 100 m/s (ordres de grandeur). Durant cette phase le bouclier thermique avant est largué : sa fonction de protection est terminée et il constitue une masse peu souhaitée. D'autres systèmes peuvent également être largués, par exemple les lests utilisés sur Mars Science Laboratory pour créer un balourd et pouvant créer un problème de non-verticalité lors de l'approche du sol.
La partie atterrissage peut utiliser des techniques différentes : amerrissage (toutes les capsules habitées américaines), rétro-fusées avec bras articulés amortisseurs (Viking) ou sans (Soyouz), airbags (Mars Pathfinder) et dans le cas de Mars Science Laboratory une technique originale faisant appel à un porteur muni de propulseurs qui dépose la charge utile (en l'occurrence le robot) par l'intermédiaire d'un filin.
Transferts d'énergie
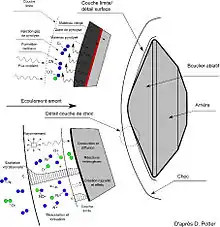
La majeure partie de la chaleur générée est due à la compression rapide de l'air à l'avant du vaisseau spatial. En comparaison, la chaleur générée par la friction entre l'air et la surface du vaisseau est minimale[16]. L'une des difficultés majeures de la rentrée réside dans les grandes quantités d'énergie qui sont dissipées et dont une partie sera convectée ou rayonnée vers la surface, échauffant celle-ci jusqu'à des valeurs élevées. Cette partie est faible, inférieure à 10 %. Une autre partie se retrouvera sous forme mécanique (onde de choc), l'essentiel étant transféré sous forme thermique ou rayonnante dans l'atmosphère environnante. Pour un objet dont la vitesse finale est faible, cette énergie est l'énergie cinétique initiale 1/2mV02. Dans l'exemple du superbolide de Tcheliabinsk, cela représente 2.2 1015 J soit l'équivalent de 0,6 megatonne de TNT. La part cédée au corps sera transformée en réactions chimiques superficielles, changement de phase et échauffement. Cet échauffement va provoquer des contraintes thermomécaniques qui pourront fissurer le matériau lorsque les contraintes induites seront supérieures aux contraintes supportables. Pour un météoroïde, cela se traduira par une désagrégation. La météorite de Tcheliabinsk s'est ainsi fragmentée entre 43 et 21 km avec un maximum d'évènements entre 30 et 37 km[11].
Les ondes de choc associées à la rentrée atmosphérique de ces objets (« bangs supersoniques ») se propagent et peuvent être assez puissantes pour provoquer des dégâts lorsqu'elles atteignent le sol. Le terme d'explosion souvent employé pour décrire ce phénomène est impropre et l'onde de choc est présente même en l'absence de fragmentation.
Haute altitude : les phénomènes liés à la raréfaction
Au-delà de 90 km d'altitude (dans l'atmosphère terrestre), le libre parcours moyen des molécules dépasse le centimètre. L'écoulement d'un tel milieu fait appel à la théorie cinétique des gaz. Les échanges d'énergie étant très faibles, ceci concerne la modification d'attitude ou des objets de grandes dimensions (structures déployables) ainsi que l'aérocapture.
Phase principale : gaz hors d'équilibre thermodynamique et réactions chimiques
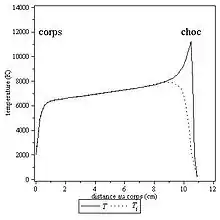
L'énergie est transférée à la paroi avec un certain débit : la densité de flux de chaleur. Celle-ci est d'origine convective et radiative, ce dernier mode pouvant être négligeable pour les faibles vitesses. Le flux convectif étant dépendant de la paroi, on évaluera un flux de référence sur paroi froide et inerte souvent nommé flux de chaleur sans autre précision.
L'objet rentrant crée une onde de choc intense qui provoque presque instantanément une augmentation de la température jusqu'à 10 000 ou 15 000 K. Derrière l'onde de choc, le milieu est hors équilibre thermodynamique et est le siège d'intenses réactions chimiques. Le milieu est décrit par plusieurs températures correspondantes aux divers degrés de liberté du gaz. Les modèles les plus simples se cantonnent à deux températures. La première est relative à la translation des particules lourdes (molécules, atomes et ions) et est liée à la statistique de Maxwell. La seconde décrit les énergies internes (statistique de Boltzmann). La température de rotation des molécules est égale à la température de translation et la température des électrons libres égale à celle des énergies internes[17].
Les collisions ramènent vers l'équilibre thermodynamique qui est généralement atteint avant le corps mais le milieu reste assez chaud pour que perdurent les réactions chimiques, typiquement 4 000 à 6 000 K au voisinage de la couche limite. Les flux de chaleur convectifs sont très souvent évalués en ne conservant de cette physique complexe que les réactions chimiques. C'est ainsi que des méthodes approchées ont été mises au point, permettant une estimation aisée du flux pariétal au point d'arrêt, telle que la méthode de Sutton et Graves conduisant à l'expression suivante[18] :
R est le rayon du corps au voisinage de l'axe de symétrie et a une constante caractéristique de l'atmosphère. a=1.83 10-4 kg-1/2 m-1 pour l'atmosphère terrestre, a=1.35 10-4 kg-1/2 m-1 pour celle de Mars. La précision est de l'ordre de 10 %. On remarque la dépendance en R-1/2 liée au gradient de vitesse de l'écoulement sur le corps. Le flux décroît lorsque l'on augmente le rayon.
En reprenant la méthode utilisée ci-dessus pour la cinématique, on peut calculer l'altitude du flux maximal
et sa valeur
Dans le cas de l'exemple de Stardust R=0,220 m d'où un flux maximal de 9,8 MW/m2 à une altitude de 57 km. La valeur exacte calculée par des méthodes plus précises est 10,2 MW/m2[19]. Cette valeur est considérable. Si on veut estimer ses effets on peut calculer la température qu'atteindrait une paroi d'émissivité égale à 1 soumise à ce flux. Cette valeur est donnée par la relation d'équilibre de rayonnement soit 3630 K. Il n'existe aucun matériau capable de résister à cette température en atmosphère oxydante. C'est pourquoi on fait appel à un bouclier thermique ablatif. Le choix du matériau sera lié à qmax tandis que son épaisseur sera liée à l'énergie surfacique
On remarque que cette quantité varie comme alors que le flux maximal varie comme . Dans le cas de Stardust l'énergie surfacique atteint 190 MJ/m2
Rayonnement
Aux vitesses modérées (V < 15 000 m/s)
Le rayonnement émis par un gaz augmente très vite avec la température. Dans le cas de l'air, le passage de 5 000 K (voisinage de la paroi) à 10 000 K (immédiatement derrière le choc) produit une augmentation de l'énergie émise d'un facteur 104 environ[20]. Il faut atteindre dans l'atmosphère terrestre des vitesses supérieures à 10 km/s pour que ce phénomène devienne important. Dans le cas de la rentrée sur Titan, le rayonnement a été notable malgré la vitesse modeste. Ceci est lié à la présence d'hydrocarbures dans l'atmosphère de ce satellite. En arrivant dans la région la plus chaude de l'écoulement, il se crée des espèces chimiques ayant un fort pouvoir émissif, par exemple le radical CN. Ces espèces sont également présentes dans tous les cas dans la couche limite du fait de la dégradation de l'écran thermique mais elles sont confinées dans des régions plus froides et donc n'émettent que peu.
Ce type de phénomène se prête assez peu au calcul approché comme celui fait ci-dessus pour la convection. Il existe cependant des corrélations permettant de calculer une valeur approximative du flux pariétal. Elles sont de la forme[21]
P(V) est un polynôme d'approximation qui varie rapidement avec V, ceci traduisant l'évolution de l'émission avec la température. Dans l'exemple de Stardust, ceci conduit à une valeur maximale de 1,9 MW/m2, c'est-à-dire une valeur non négligeable comparée au flux convectif calculé ci-dessus qui est, rappelons-le, une valeur sur paroi froide et inerte donc majorant la valeur réelle dépendante de l'écran thermique. Il existe également une corrélation plus simple et moins précise due à Detra et Hidalgo[22] :
Pour cette dernière, on peut comme ci-dessus calculer l'altitude correspondante au maximum de flux radiatif : , valeur peu différente de celle obtenue pour le flux convectif. Cette expression est valide pour un milieu transparent dans lequel la quantité d'énergie émise est proportionnelle à l'épaisseur du domaine qui émet, laquelle est directement proportionnelle au rayon par invariance par homothétie des équations d'Euler. Ces corrélations sont limitées à un domaine relativement limité ; en particulier, elles ne sont pas applicables pour des vitesses notablement supérieures à 16 km/s. Pour les très grandes vitesses telle que les entrées de météoroïdes, il se crée un fort couplage entre rayonnement et convection : le rayonnement abaisse la température du gaz et diminue l'épaisseur de la couche de choc, entraînant une auto-limitation des flux convectif et radiatif. Le rayonnement devient rapidement le mode de transfert prépondérant. Cet effet peut être estimé à partir du nombre de Goulard . Le couplage devient notable dès que cette quantité atteint quelques pourcents. Le flux radiatif couplé vaut alors environ[23] :
a=3,45 pour l'air, 3 pour l'atmosphère de Jupiter, 2 pour celle de Titan. Bien que la corrélation ci-dessus ne soit pas valable pour les petits rayons on peut néanmoins noter que la tendance rend difficile l'expérience sur une maquette d'essai (tube à choc, tunnel de tir ou torche à plasma) du fait du faible rayon utilisable dans ces installations.
Aux très grandes vitesses (V > 15 000 m/s)
La vitesse de rentrée dans l'atmosphère terrestre des météoroïdes peut dépasser 70 km/s. Pour des objets de taille métrique ou plus et des vitesses supérieures à 15 km/s, le milieu est totalement ionisé et le rayonnement devient prépondérant[24]. Il modifie notablement l'écoulement en créant une perte d'énergie entre le choc et la paroi, entraînant une diminution d'enthalpie et donc du flux convectif. Les températures atteignent tout de même quelques dizaines de milliers de degrés, voire dépassent 100 000 K. Elles sont à l'origine d'un intense rayonnement, en particulier dans le domaine ultraviolet. Cette partie du rayonnement est absorbée par le dioxygène environnant et crée un précurseur en avant de l'onde de choc dans lequel la température atteint quelques milliers de degrés. Ce préchauffage du gaz augmente d'autant la température derrière le choc (relations de Rankine-Hugoniot).
Le problème des poussières sur Mars
Périodiquement, le vent sur Mars crée des nuages de particules d'un diamètre de quelques dizaines de microns qui s'élèvent jusqu'à 60 km d'altitude[25]. Un tel évènement peut intéresser de larges régions géographiques et même, quelques fois par décennie, recouvrir entièrement la planète[26].
Parmi ces particules présentes à certains moments dans l'atmosphère de Mars, les plus grosses ont une masse trop forte pour être mise en mouvement à l'approche du vaisseau spatial et chassées par l'écoulement qui tend à contourner le vaisseau[27]. Elles percutent donc la surface avec des vitesses de plusieurs km/s (~ la vitesse du vaisseau). Dans ce type de collisions, chaque particule enlève au bouclier thermique une masse de plusieurs dizaines de fois la sienne[10]. Cela peut conduire à la destruction de la sonde. Il faut noter de plus que ce phénomène est très difficile à simuler et tout autant à tester ; il constitue un risque pour toute mission martienne.
Le phénomène de black-out
La transmission des ondes électromagnétiques peut être déphasée, bruitée, affaiblie, voire interrompue durant la rentrée : c'est le phénomène de black-out. Celui-ci est dû à l'interaction des ondes avec les électrons présents dans le milieu. La propagation est interrompue lorsque la fréquence est inférieure à une fréquence caractéristique du milieu ionisé : la fréquence propre du plasma. À partir de celle-ci, on peut calculer la densité électronique provoquant la coupure pour une fréquence f :
avec . À ce phénomène d'écrantage se superpose un autre problème lié à la désadaptation des antennes due à la modification de la permittivité du milieu proche de celle-ci.
Si l'on prend une fréquence dans la bande X telle qu'utilisée pour Pathfinder vers 10 GHz, la densité électronique de coupure vaudra environ 1012 /m3. Ces valeurs ont été atteintes durant les 30 s de coupure totale du signal. Sur les vols Apollo, le black-out dure environ trois minutes.
Les densités électroniques sont très variables à un instant donné sur le corps. Le concepteur cherche donc à optimiser la position des antennes pour minimiser ce phénomène en tenant compte de diverses contraintes d'implantation. Le problème a été résolu sur la navette spatiale en émettant vers le haut en direction d'un satellite servant de relais, traversant ainsi une région de l'écoulement faiblement ionisée.
Structures déployables
Des structures déployables ont été imaginées pour augmenter notablement la traînée. Elles sont destinées à l'entrée sur Mars où la faible pression au sol limite les régions accessibles aux zones de faible altitude. Parmi ces structures, on peut citer les ballutes et les décélérateurs supersoniques. Ces derniers ont fait l'objet de développements de la part de l'ESA et de la NASA.
Notes et références
- ↑ (en) « Coming Home. Reentry and Recovery from Space. ».
- ↑ (en) « National Aeronautics and Space Administration ».
- ↑ (en) « Russian Federal Space Agency ».
- ↑ (en) « Japan Aerospace Exploration Agency ».
- ↑ (en) « Indian Space Research Organisation ».
- ↑ (en) « China National Space Administration ».
- ↑ (en) « European Space Agency ».
- ↑ (en) Ball A. J., Garry J. R. C., Lorenz R. D. et Kerzhanovich V. V., Planetary Landers and Entry Probes, Cambridge University Press, (ISBN 978-0-521-12958-9).
- ↑ (en) C. A. Davies et M. Arcadi, « Planetary Missions Entry Vehicles. Quick Reference Guide. », NASA Technical Report SP-2006-3401, (lire en ligne).
- 1 2 (en) Duffa G., Ablative Thermal Protection Systems Modeling, Reston, VA, AIAA Educational Series, , 431 p. (ISBN 978-1-62410-171-7).
- 1 2 (en) Jiří Borovička, Pavel Spurný, Peter Brown, Paul Wiegert, Pavel Kalenda, David Clark et Lukáš Shrbený, « The trajectory, structure and origin of the Chelyabinsk asteroidal impactor », Nature Letter, vol. 503, , p. 235-237.
- ↑ (en) F. W. Leslie et C. G. Justus, « The NASA Marshall Space Flight Center Earth Global Reference Atmospheric Model-2010 Version », NASA TM-2011-216467, (lire en ligne).
- ↑ (en) « NGA/NASA EGM96, N=M=360 Earth Gravitational Model », .
- ↑ (en) W. A. Wood, « Hypersonic Pitching-Moment Shift for Stardust Reentry Capsule Forebody », NASA Technical Report TM-97-206266, (lire en ligne).
- ↑ (en) Gallais P., Atmospheric Re-Entry Vehicle Mechanics, Berlin, Springer Verlag, , 353 p. (ISBN 978-3-540-73646-2).
- ↑ (en) « NASA - NASA Developing New Heat Shield for Orion », sur www.nasa.gov (consulté le ).
- ↑ Brun R., Introduction à la dynamique des gaz réactifs, Toulouse, Cépaduès, , 364 p. (ISBN 978-2-36493-057-5).
- ↑ (en) K. Sutton et R. A. Graves, « A General Stagnation-Point Convective-Heating Equation for Arbitrary Gas Mixtures », NASA Technical Report TR-R-376, (lire en ligne).
- ↑ (en) Olynick D., Chen Y.-K. et Tauber M. E., « Forebody TPS Sizing with Radiation and Ablation for the Stardust Sample Return Capsule », AIAA 32nd Thermophysics Conference, .
- ↑ (en) M.-Y. Perrin, P. Rivière et A. Soufiani, « Radiation Database for Earth and Mars Entry », Rapport RTO-EN-AVT-162, (lire en ligne).
- ↑ (en) M. E. Tauber et K. Sutton, « Stagnation Point Radiative Heating Relations for Earth and Mars », Journal of Spacecraft and Rockets, vol. 28, 6, , p. 40-42.
- ↑ (en) R. W. Detra et H. Hidalgo, « Generalized Heat Transfer Formulae and Graphs for Nose-Cone Re-entry in the Atmosphere », ARS Journal, vol. 31, , p. 318-321.
- ↑ (en) M. E. Tauber et R. Wakefield, « Heating Environment and Protection during Jupiter Entry », Journal of Spacecraft and Rockets, vol. 8, 3, , p. 630-636.
- ↑ (en) G. Duffa, « Meteors entry phenomenology and modeling », Hypersonic Meteoroid Entry Physics (HyMEP) Course, (lire en ligne).
- ↑ (en) Howard A. Perko, John D. Nelson et Jaklyn R. Green, « Review of Martian Dust Composition, Transport, Deposition, Adhesion, and Removal », Eighth International Conference on Engineering, Construction, Operation, and Business In Space, (lire en ligne).
- ↑ (en) « The Perfect Dust Storm Strikes Mars », .
- ↑ Le problème est à rapprocher de celui des insectes qui, sur Terre, se présentent face à une automobile à grande vitesse. Les insectes qui ne sont pas déviés par l'écoulement autour de l’automobile (ils passent à travers les lignes de courant) s'écrasent sur la face avant de l'automobile. Ces écrasements sont évidemment plus nombreux autour de la calandre mais certains se produisent sur le pare-brise.
Articles connexes
- Atmosphère terrestre
- Atmosphère de Mars
- Atmosphère de Vénus
- Atmosphère de Titan
- Atmosphère de Jupiter
- Champ gravitationnel
- Géodésie
- Bouclier thermique
- Aérodynamique
- Aérofreinage
- Ballute
- Low-Density Supersonic Decelerator
- Rebond atmosphérique










































