مجموع ريمان

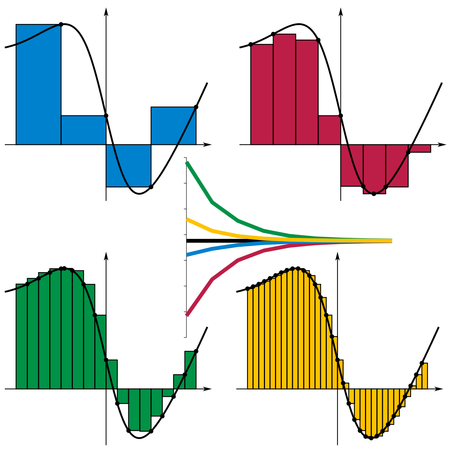
أربعة من طرق الجمع لريمان من أجل الاقتراب من قيمة المساحة الموجودة تحت المنحنى. طريقتا اليمين و اليسار تقتربان من المساحة المطلوبة باستعمال الحدين الأيمن والأيسر من كل مجال جزئي، على التوالي.^[1][2] Maximum and minimum methods make the approximation using the largest and smallest endpoint values of each subinterval, respectively. The values of the sums converge as the subintervals halve from top-left to bottom-right.

تعريف

لتكن f : D → R دالة معرفة على مجموعة جزئية، D، من مستقيم الأعداد الحقيقية، R. ليكن [I = [a، b مجالا مغلقا ضمن D، ولتكن

${\displaystyle P=\left\{[x_{0},x_{1}],[x_{1},x_{2}],\dots ,[x_{n-1},x_{n}]\right\},}$

تجزئة ل I, حيث

${\displaystyle a=x_{0}<x_{1}<x_{2}<\cdots <x_{n}=b.}$

مجموع ريمان ل f على I طبقا للتجزئة P يعرف كما يلي

${\displaystyle S=\sum _{i=1}^{n}f(x_{i}^{*})(x_{i}-x_{i-1}),\quad x_{i-1}\leq x_{i}^{*}\leq x_{i}.}$

لاختيار ${\displaystyle x_{i}^{*}}$ في المجال ${\displaystyle [x_{i-1},x_{i}]}$ عديد من الإمكانيات.

مثال: اختيار ${\displaystyle x_{i}^{*}}$ يعطي مختلف الأنواع من مجاميع ريمان:

• إذا ${\displaystyle x_{i}^{*}=x_{i-1}}$ مهما كان i, إذن S يسمى مجموع ريمان اليساري.
• إذا ${\displaystyle x_{i}^{*}=x_{i}}$ مهما كان i, إذن S يسمى مجموع ريمان اليميني.
• إذا ${\displaystyle x_{i}^{*}={\tfrac {1}{2}}(x_{i}+x_{i-1})}$ مهما كان i, إذن S يسمى مجموع ريمان الوسطي.
• متوسط مجموعي ريمان اليساري واليميني يسمى المجموع شبه المنحرفي.
• إذا it is given that

${\displaystyle S=\sum _{i=1}^{n}v_{i}(x_{i}-x_{i-1}),}$

where ${\displaystyle v_{i}}$ is the supremum of f على ${\displaystyle [x_{i-1},x_{i}]}$, then S is defined to be an مجموع ريمان العُلوي.

• Similarly, إذا ${\displaystyle v_{i}}$ is the infimum of f على ${\displaystyle [x_{i-1},x_{i}]}$, then S is a lower Riemann sum.

الطرق

المجموع في اليسار

اليمين

الوسط

قاعدة شبه المنحرف

أمثلة

التأويل الهندسي لمجموع ريمان

• 

  مجموع من اليسار

• 

  مجموع من اليمين

• 

  مجموع من الوسط

• 

  مع ${\displaystyle y=x^{2}}$

مقالات ذات صلة

• طريقة أويلر، طريقة من أجل حلحلة المعادلات التفاضلية.

مراجع

وصلات خارجية

• محاكاة تظهر تقريب مجاميع ريمان

موسوعات ذات صلة :

• موسوعة تحليل رياضي