Le plus petit corps

Le plus petit corps fini est noté F₂. Il est composé de deux éléments distincts, 0 qui est l'élément neutre pour l'addition, et 1 qui est élément neutre pour la multiplication. Ceci détermine les tables de ces deux opérations en dehors de 1+1 qui ne peut alors être que 0, car 1 doit avoir un opposé. On vérifie alors qu'elles définissent bien un corps commutatif.

Le corps F₂ peut s'interpréter diversement. C'est l'anneau Z/2Z, les entiers pris modulo 2, c'est-à-dire que 0 représente les entiers pairs, 1 les entiers impairs (c'est le reste de leur division par 2), et les opérations se déduisent de celles sur Z.

C'est aussi l'ensemble des valeurs de vérité classiques, 0 pour le faux, et 1 pour le vrai. L'addition est le « ou exclusif » (xor), la multiplication le « et »^[3].

Les fonctions de (F₂)ⁿ dans F₂ sont appelées fonctions booléennes^[4]. La disjonction (inclusive) et la négation se définissent ainsi :

Plus généralement on déduit du théorème d'interpolation de Lagrange que toutes les fonctions booléennes sont polynomiales (c'est une propriété qui passe à n'importe quel corps fini).

Corps premiers finis

Une généralisation naturelle de F₂ = Z/2Z est, pour p premier, le corps Z/pZ à p éléments, noté aussi F_p :

Proposition. — L'anneau Z/nZ est un corps si et seulement si n est un nombre premier.

En effet, p est premier équivaut à ce que 0 ne soit pas produit de deux entiers non nuls modulo p, par le lemme d'Euclide. Il faut donc que p soit premier pour que Z/pZ soit un corps. De plus, ceci assure que si p est premier, Z/pZ est intègre et partant, comme il est fini, un corps. L'identité de Bézout assure directement l'existence d'un inverse, et un calcul efficace de celui-ci par l'algorithme d'Euclide étendu.

Le groupe multiplicatif de Z/pZ (p premier) est d'ordre p – 1 ce qui conduit au petit théorème de Fermat par le théorème de Lagrange. On montre que ce groupe est cyclique (la démonstration est la même que dans le cas général, traité au paragraphe Groupe multiplicatif et conséquences)^[5].

On verra que pour tout nombre premier p, Z/pZ est à isomorphisme près le seul corps de cardinal p, et qu'il ne contient pas d'autre sous-corps que lui-même. Un tel corps est appelé corps premier, et les Z/pZ, p premier, sont les seuls corps premiers finis.

Quotient par un polynôme irréductible

Pour construire de nouveaux corps finis, on utilise la structure d'anneau euclidien de F_p[X] de la même façon que l'on a utilisé celle de Z pour construire les corps premiers. Les polynômes irréductibles jouent le rôle des nombres premiers. Deux polynômes sont équivalents modulo le polynôme P s'ils ont même reste par division par celui-ci. Le quotient par la relation d'équivalence obtenue est noté F_p[X]/(P), où (P) := P F_p[X], la structure induite par quotient est encore celle d'un anneau^[6].

On a de façon strictement analogue au cas des entiers :

Proposition. — L'anneau F_p[X]/(P) est un corps si et seulement si P est un polynôme irréductible.

Soit n le degré de P. La propriété d'unicité du reste de la division polynomiale se traduit par le fait que chaque élément de F_p[X]/(P) est représenté par un unique polynôme de degré < n. Le cardinal de F_p[X]/(P) est donc pⁿ. Pour construire un corps fini de cardinal pⁿ, il suffit donc de trouver un polynôme irréductible de degré n dans F_p[X].

Si P est irréductible, le quotient K = F_p[X]/(P) est alors un corps de rupture du polynôme P, car la classe de X est une racine de P dans K.

Pour ces constructions il est indispensable que les polynômes soient des polynômes formels, et non des fonctions polynomiales. Il existe en effet des polynômes non-nuls dont les fonctions polynomiales associées sont identiquement nulles sur F_p (par exemple X + X² sur F₂). Une autre manière de se rendre compte de la différence est qu'il ne peut exister qu'un nombre fini de fonctions de F_p dans F_p et donc de fonctions polynomiales, alors qu'il existe un nombre infini de polynômes formels.

Exemple : les corps à p² éléments

On peut donc construire les corps à p² éléments, en montrant qu'il existe un polynôme irréductible P de degré 2 dans F_p[X]. Le corps F_p[X]/(P), possède p² éléments, et c'est une extension quadratique de F_p. On verra plus loin que le corps à p² éléments est unique (à isomorphisme près) et on le notera F_p². En particulier, le corps que nous allons construire est en fait indépendant du choix du polynôme irréductible P de degré 2 utilisé pour le quotient. Cette extension quadratique de F_p est l'analogue de l'(unique) extension quadratique du corps des nombres réels, qui donne le corps des nombres complexes.

• Pour p = 2, le polynôme 1 + X + X² est irréductible dans F₂[X] (c'est d'ailleurs le seul polynôme irréductible de degré 2 sur F₂). L'extension correspondante est un corps noté F₄. Ce corps a exactement 4 éléments qui sont 0, 1, et les deux racines φ et φ² = φ + 1 de 1 + X + X². Ses lois sont alors :

• Quand p est premier impair, un polynôme de la forme X² – a est irréductible si et seulement si a n'est pas un carré. Or pour p différent de 2, il existe dans F_p des éléments non carrés. En effet, les carrés des p – 1 éléments non nuls de F_p sont au nombre de (p – 1)/2 (chaque carré non nul est le carré d'exactement deux éléments, opposés l'un de l'autre), donc il reste (p – 1)/2 éléments non carrés, parmi lesquels on peut choisir a. Pour p congru à 3 modulo 4, dans ce cas p est nombre premier de Gauss, on peut même choisir simplement a = –1 (voir l'article Théorème des deux carrés de Fermat ou l'article Loi de réciprocité quadratique), si bien que F_p² est isomorphe au corps Z[i]/pZ[i], car ils ont le même cardinal.

Caractéristique et cardinal

Soit K un corps fini, 0_K et 1_K les éléments neutres additif et multiplicatif. On note n.1_K le résultat de l'addition de 1_K itérée n fois. L'application correspondante est compatible avec l'addition et la multiplication (c'est l'unique morphisme d'anneaux (unitaires) de Z dans K). La caractéristique du corps K est le plus petit entier p > 0 tel que p.1_K = 0_K (un tel nombre existe car le groupe additif engendré par 1_K est fini). De plus, p est un nombre premier. En effet, si a et b sont des entiers tels que ab = p, alors (a.1_K)(b.1_K) = (ab).1_K = 0_K. Comme K est un corps, a.1_K ou b.1_K est nul, et donc par définition de p, a ou b vaut p. On vérifie alors que l'homomorphisme de Z dans K qui à n associe n.1_K induit une injection de Z/p Z dans K, son image est un sous-corps de K isomorphe à Z/p Z. Il est contenu dans tout sous corps de K (qui doit contenir 0_K et 1_K). C'est donc le plus petit sous-corps de K et on le nomme sous-corps premier de K^[8]. Pour la même raison c'est le seul sous-corps de K isomorphe à Z/p Z, et on peut l'identifier à Z/p Z (= F_p).

Si L est un sous-corps de K, dit autrement si K est une extension de L, K possède naturellement une structure d'espace vectoriel sur L, l'addition et la multiplication externe étant celles de K. Dans le cas des corps finis, sa dimension est nécessairement finie. Le cardinal de K est alors pⁿ, où n est la dimension de K comme espace vectoriel sur son sous-corps premier F_p. De façon générale le cardinal d'un sous-corps L de K est de la forme p^d, et comme K est aussi un espace vectoriel sur L, d est un diviseur de n. On a donc :

Proposition. — Le cardinal d'un corps fini K est une puissance d'un nombre premier p qui est sa caractéristique. De plus, si ce corps est de cardinal pⁿ, tout sous-corps de K est de cardinal p^d où d divise n^[9].

Automorphisme de Frobenius

Soit K un corps fini de caractéristique p, de cardinal q = pⁿ. Comme p est premier, p divise chacun des coefficients binomiaux ${\displaystyle {\tbinom {p}{i}}}$ pour 0 < i < p. On a donc :

${\displaystyle (x+y)^{p}=x^{p}+y^{p}}$.

On en déduit (l'image de 1_K est 1_K, la compatibilité avec la multiplication est immédiate) que l'application de K dans lui-même qui à x, associe x^p est un endomorphisme de corps, donc injectif, qui laisse stable le sous-corps premier (c'est le petit théorème de Fermat). Il est appelé endomorphisme de Frobenius. Le corps étant fini, l'endomorphisme est bijectif.

Il est simple de vérifier que l'ensemble des points fixes par un automorphisme dans un corps est un sous-corps, et dans le cas de l'automorphisme de Frobenius, ce sous-corps est par définition l'ensemble des racines du polynôme X^p – X, de cardinal au plus p, donc c'est le sous-corps premier de K^[10].

On verra plus loin que les automorphismes d'un corps fini sont tous des itérés de l'automorphisme de Frobenius.

Existence et unicité d'un corps fini de cardinal pⁿ

Soit K un corps fini de cardinal q = pⁿ. Alors, K*, le groupe multiplicatif de ce corps est de cardinal q – 1. On déduit du théorème de Lagrange que tout élément de K* est racine du polynôme X^q–1 – 1, et donc tout corps de cardinal q est un corps de décomposition du polynôme X^q – X sur F_p. Par conséquent (propriété des corps de décomposition), deux corps de cardinal q sont isomorphes.

Soit maintenant n un entier strictement positif, q l'entier égal à pⁿ et K le corps de décomposition du polynôme P(X) = X^q – X sur le corps F_p. L'ensemble des racines de X^q – X dans K est l'ensemble des points fixes de l'automorphisme de Frobenius itéré n fois (q = pⁿ). Il forme donc un sous-corps de K, et c'est K par définition d'un corps de décomposition. Or le polynôme dérivé de P(X) = X^q – X est P’(X) = q X^q–1 – 1 = –1 qui est constant non nul ; X^q – X n'a donc pas de racine multiple (si Q² divise P, Q divise P’) : il possède q racines distinctes. Le corps K a donc pour cardinal q = pⁿ. En résumé^[10] :

Proposition. — Il existe un corps de cardinal q = pⁿ, et un seul à isomorphisme près, noté F_q. Une clôture algébrique de F_p contient un seul corps de cardinal q qui est le corps de décomposition de X^q – X.

On dit que « le » corps à q éléments est essentiellement unique : deux corps à q éléments sont isomorphes, mais il n'y a pas unicité de l'isomorphisme (voir infra).

Le corps de décomposition du polynôme P se construit dans le cas le plus général en itérant la construction d'un corps de rupture sur un facteur de P irréductible de degré au moins deux dans le corps déjà obtenu. Pour des raisons de cardinalité, il suffit de trouver un facteur irréductible de degré n de X^pn – X pour obtenir en un pas son corps de décomposition. La suite montre qu'il existe de tels facteurs. On peut d'ailleurs déduire l'existence et l'unicité à isomorphisme près d'un corps fini de cardinal pⁿ simplement de l'existence et l'unicité à isomorphisme près d'un corps de rupture, si on a une preuve directe de l'existence d'un polynôme irréductible de degré n sur F_p^[11].

Soit maintenant d un diviseur de n. Supposons qu'il existe un sous-corps de F_q (q = pⁿ) à p^d éléments. Alors, pour les mêmes raisons que ci-dessus, ce corps est le corps de décomposition dans F_q du polynôme X^pd – X, et donc il existe au plus un sous-corps de cardinal p^d. Un tel corps de décomposition existe dans F_q, car le polynôme X^pd – X, qui divise X^pn – X, est scindé sur F_q. En résumé :

Proposition. — Soit F_q un corps fini de caractéristique p, de cardinal q = pⁿ. Alors pour tout diviseur d de n il existe un unique sous-corps de F_q de cardinal p^d, et ce sont les seuls sous-corps de F_q.

Groupe multiplicatif et conséquences

On a déjà utilisé une propriété élémentaire du groupe multiplicatif d'un corps fini au paragraphe précédent. On peut préciser sa structure. Le groupe (F_q*, ×) est un groupe abélien fini donc son exposant e est l'ordre d'au moins un élément x du groupe. Or le polynôme X^e – 1, de degré e, possède q – 1 racines distinctes dans F_q, ce qui implique que e est supérieur à q – 1. On en déduit que le sous-groupe de F_q* engendré par x est égal au groupe tout entier^[12] :

Proposition. — Le groupe multiplicatif d'un corps fini est cyclique.

On appelle élément primitif de F_q un générateur de son groupe multiplicatif (c'est une racine primitive de l'unité d'ordre q – 1)^[13]. On en déduit que tout corps fini F_q est l'extension de son sous-corps premier (ou de n'importe lequel de ses sous-corps) définie par adjonction d'un élément primitif α.

Proposition. — Dans tout corps fini F_q de caractéristique p, il existe un élément α tel que F_q = F_p[α].

On appelle aussi élément primitif sur F_p un élément α vérifiant cette propriété^[14]. Mais il peut exister des éléments primitifs en ce sens qui ne le sont pas au sens précédent (voir ci-dessous). C'est la première définition qui est utilisée dans la suite de l'article.

En prenant q = pⁿ, et α un élément primitif de F_q, on déduit de la proposition qu'il existe en effet un polynôme P irréductible de degré n qui annule α et F_q est un corps de rupture de P (voir l'article lié). En particulier, pour tout entier n, il existe polynôme irréductible de degré n sur tout corps fini premier (et d'ailleurs sur tout corps fini en suivant le même raisonnement).

Un tel polynôme unitaire irréductible P qui annule α est appelé polynôme minimal de α (ils sont étudiés dans une section suivante). Quand α est un élément primitif de F_q, on vérifie que les n racines de P sont les images par l'automorphisme de Frobenius itéré de 0 à n – 1, soient α, α^p, α^p2, ..., α^pn–1, et sont distinctes car une égalité entre deux de celles-ci contredirait que α est primitif ; F_q est donc un corps de rupture, mais aussi un corps de décomposition de P.

Un automorphisme de corps de F_q laisse nécessairement invariants les éléments du sous-corps premier. L'image de α par un tel automorphisme est encore une racine de P, donc de la forme α^pi. Cette image détermine l'automorphisme, α étant primitif, qui est donc un itéré de l'automorphisme de Frobenius.

Proposition. — Le groupe des automorphismes d'un corps fini F_pⁿ de caractéristique p est le groupe cyclique d'ordre n engendré par l'automorphisme de Frobenius qui à x associe x^p.

Théorie de Galois

Les propriétés précédentes peuvent être revues à la lumière de la théorie des corps commutatifs et de la théorie de Galois.

Un corps fini est parfait, c'est-à-dire que ses extensions algébriques sont séparables. C'est une conséquence du fait que l'endomorphisme de Frobenius est bijectif (voir l'article lié, ou, toute extension algébrique finie étant un corps fini, l'étude des polynômes irréductibles faite plus loin).

Le corps F_pⁿ est, d'après le paragraphe précédent, isomorphe au corps de décomposition d'un polynôme de degré n séparable sur F_p. C'est donc une extension galoisienne de F_p.

Le groupe des automorphismes d'un corps fini est son groupe de Galois sur son sous-corps premier. On a vu qu'il était cyclique ; ses sous-groupes sont les groupes cycliques d'ordre un diviseur de n. Les sous-corps ont été déterminés comme les sous-ensembles invariants par les générateurs de ces sous-groupes. C'est dans ce cas particulier le théorème fondamental de la théorie de Galois.

Clôture algébrique

On connaît par ce qui précède toutes les extensions finies, et donc, par réunion, toutes les extensions algébriques des corps finis. Toute clôture algébrique ${\displaystyle \mathbb {F} _{p}^{\mathrm {alg} }}$ de ${\displaystyle \mathbb {F} _{p}}$ peut être vue comme le compositum des ${\displaystyle \mathbb {F} _{p^{n}}}$.

Du point de vue de la théorie de Galois, la famille des groupes ${\displaystyle \mathrm {Gal} (\mathbb {F} _{p^{n}}/\mathbb {F} _{p})}$, pour n variant, forme donc ce qu'on appelle un système projectif, c'est-à-dire que le groupe de Galois absolu ${\displaystyle \mathrm {Gal} (\mathbb {F} _{p}^{\mathrm {alg} }/\mathbb {F} _{p})}$ est la limite projective des groupes ${\displaystyle \mathrm {Gal} (\mathbb {F} _{p^{n}}/\mathbb {F} _{p})\simeq \mathbb {Z} /n\mathbb {Z} }$ ; c'est donc le complété profini ${\displaystyle {\hat {\mathbb {Z} }}}$ de ${\displaystyle \mathbb {Z} }$, qui est ainsi un groupe procyclique : un générateur naturel est à nouveau l'endomorphisme de Frobenius, qui peut être vu comme la donnée de la famille compatible des endomorphismes de Frobenius des extensions finies.

Cette description complète des extensions algébriques des corps finis est un élément important qui intervient dans la théorie des corps de classes pour les corps de nombres et les corps de nombres p-adiques, car leurs corps résiduels sont des corps finis.

Un critère d'irréductibilité

Si deux polynômes P et Q de K[X] possèdent une racine commune dans une extension L de K, et si P est irréductible, alors P divise Q. En effet, sinon ces polynômes seraient premiers entre eux ce qui passerait à L par l'identité de Bézout^[15]. Ce résultat préliminaire est utile pour établir :

Proposition. — Soient F_q un corps fini à q éléments et n un entier strictement positif. Dans F_q[X], le polynôme X ^qn – X est égal au produit de tous les polynômes unitaires irréductibles de degré divisant n.

En notant m_d(q) le nombre de polynômes unitaires irréductibles de degré d sur F_q, l'égalité des degrés, dans l'égalité polynomiale de la proposition, donne :

${\displaystyle q^{n}=\sum _{d|n}d\,m_{d}(q)}$

Cette proposition permet donc de montrer l'existence de polynômes irréductibles de degré n quelconque dans F_q[X] via l'encadrement suivant^[16] :

Elle a été établie sans supposer l'existence d'un corps fini de cardinal qⁿ et la minoration (appliquée à q premier) fournit donc une autre démonstration de ce résultat^[16].

Une évaluation plus précise est possible, en inversant par la fonction de Möbius (notée μ)^[17] :

${\displaystyle m_{n}(q)={\frac {1}{n}}\sum _{d|n}\mu \left({\frac {n}{d}}\right)q^{d}.}$

La proposition fournit également une caractérisation des polynômes irréductibles qui peut être exploitée algorithmiquement^[16] :

Un polynôme P de degré n > 0 sur F_q est irréductible si et seulement si

• P divise X ^qn – X
• P est premier avec les X ^qr – X, où r = n/d, d diviseur premier de n.

Le nombre d'éléments de F_qⁿ n'appartenant à aucun de ses sous-corps stricts maximaux (les F_q^r pour de tels r) est donc nm_n(q).

Polynôme minimal

Dans un corps fini F_q, tout élément α est algébrique sur son sous-corps premier F_p (sur n'importe quel sous-corps en fait), c'est-à-dire qu'il existe un polynôme à coefficients dans F_p qui annule α (les puissances successives de α ne peuvent être indépendantes). Le polynôme unitaire à coefficients dans F_p de plus petit degré qui annule α est appelé polynôme minimal de α sur F_p^[18]. Il est nécessairement irréductible et engendre l'idéal des polynômes annulateurs de α. Les coefficients du polynôme étant invariants par l'automorphisme de Frobenius et ses itérés, les α^pi sont également des racines de ce polynôme. On montre qu'il n'y en a pas d'autre.

Proposition. — Soit P polynôme minimal de degré r sur F_p de α élément d'un corps F_q de caractéristique p. Alors toutes les racines de P sont simples et ce sont exactement :

α, α^p, α^{p 2}..., α^{p r – 1}.

Il suffit de montrer que ces r racines sont distinctes. Soient 0 < i ≤ j < r et α^pi = α^pj, alors, en élévant à la puissance idoine, α^pr–j+i = α, donc P divise X^pr–j+i – X (résultat préliminaire du paragraphe précédent), donc (proposition précédente) r divise r – j + i, donc i = j^[19].

Tout polynôme unitaire P irréductible sur F_p est le polynôme minimal de la classe de X dans son corps de rupture F_p[X]/(P), qui contient donc toutes les racines de P. La démonstration vaut pour n'importe quel corps fini (pas nécessairement premier), c'est-à-dire que

Proposition. — Le corps de rupture d'un polynôme irréductible sur un corps fini est aussi son corps de décomposition.

Les α, α^p, α^p2, ..., α^pr–1, les éléments ayant même polynôme minimal sur F_p que α, sont appelés conjugués de α par rapport à F_p^[20]. Ce sont aussi les images de α par les n automorphismes de F_q. Ces images sont distinctes si et seulement si le degré r du polynôme minimal de α égale le degré n de l'extension F_q de F_p.

Le polynôme minimal d'un élément primitif (au sens racine primitive de l'unité) de F_q est appelé polynôme primitif^[21], c'est nécessairement un polynôme irréductible de degré n dont les racines sont les n conjugués (distincts) d'une racine particulière α, soit α, α^p, α^p2, ..., α^pn–1.

On va voir dans la section suivante que les polynômes primitifs sur F_p sont aussi les facteurs irréductibles du polynôme cyclotomique d'indice pⁿ – 1 sur ce même corps.

Polynômes primitifs et polynômes cyclotomiques

Illustration graphique du groupe multiplicatif de F₄.

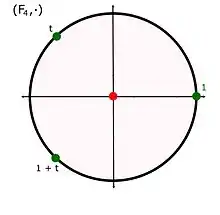
Soit p un nombre premier, n un entier strictement positif et q = pⁿ. On a déduit du théorème de Lagrange que tout élément non nul de F_q est racine de l'unité, et donc racine du polynôme X^q-1 - 1. Cette propriété est illustrée sur la figure de droite, les trois éléments non nuls de F₄ sont les trois racines de l'unité.

Les polynômes cyclotomiques étant à coefficients entiers, ils s'interprètent aussi dans les corps finis^[22], mais alors qu'ils sont irréductibles dans Q, ils ne le sont plus forcément dans un sous-corps premier F_p^[23] (voir la section Exemples). Dans Z[X], X^q–1 – 1 est le produit des polynômes cyclotomiques dont l'indice divise q – 1, et ceci passe à F_p. Par ailleurs un polynôme irréductible P de degré strictement supérieur à 1 est tel que F_p[X]/(P) est un corps fini, et P, polynôme minimal d'un élément de ce corps, divise X^q–1 – 1, donc^[24] :

• Tout polynôme irréductible de F_p[X] autre que X divise un polynôme cyclotomique.

Si φ désigne la fonction indicatrice d'Euler il existe exactement φ(q – 1) éléments primitifs dans F_q. Comme par définition ces éléments ne sont pas racines de X^d – 1, donc de Φ_d pour d < q – 1, ce sont les racines du polynôme cyclotomique Φ_{q – 1}. Les polynômes primitifs, qui sont les polynôme minimaux (sur F_p) de ces éléments primitifs, divisent donc Φ_{q – 1}.

La relation « avoir même polynôme minimal sur F_p » est une relation d'équivalence, dont chaque classe possède pour cardinal le degré du polynôme irréductible associé (voir la section #Polynôme minimal, ou plus simplement dans le cas particulier des polynômes primitifs la section #Groupe multiplicatif et conséquences). On a donc :

• le polynôme cyclotomique d'indice pⁿ – 1 est le produit des polynômes primitifs de degré n sur F_p.
• Il existe exactement φ(q – 1) éléments primitifs dans F_q, correspondant à φ(q – 1)/n polynômes primitifs sur son corps premier F_p.

On déduit en particulier de l'existence d'un corps fini de cardinal pⁿ pour tout entier n, que le polynôme cyclotomique d'indice pⁿ – 1 est toujours le produit de polynômes irréductibles de même degré n sur F_p. Ce résultat peut se démontrer directement, en utilisant seulement l'existence du corps de rupture d'un polynôme, et alors on a une autre preuve d'existence d'un corps fini de cardinal pⁿ (qui suppose connus les résultats de base sur les polynômes cyclotomiques usuels)^[25]. En fait tout polynôme cyclotomique se décompose sur F_p en facteurs irréductibles de même degré^[26].

Il peut y avoir d'autres polynômes irréductibles de degré n que les polynômes primitifs. Par exemple dans F₉, on a

et X² + 1, bien qu'irréductible, n'est le polynôme minimal d'aucun des 4 éléments primitifs (voir aussi ci-dessous l'exemple de F₁₆).

Remarque : on peut définir directement le polynôme cyclotomique d'indice r sur un corps fini K de caractéristique p pour r qui n'est pas un multiple de p, à partir des racines r-ième de l'unité dans une extension de K où X^r - 1 est scindé. Leur étude se mène alors de la même façon que celle des polynômes cyclotomiques usuels sur Q^[27].

Exemples

Caractéristique deux

Il existe sur F₂ exactement deux polynômes de degré 1, dont l'un — le polynôme cyclotomique d'indice 1 sur F₂ — est primitif :

${\displaystyle X\quad {\text{et}}\quad \Phi _{1,F_{2}}(X)=X-1.}$

Les racines du (ou des) polynôme(s) de degré 2 irréductibles sur F₂ sont les éléments de F_2² = F₄ qui n'appartiennent pas à F₂. Ce sont donc les 2 générateurs du groupe multiplicatif F₄* à trois éléments. Par conséquent, il existe en fait un unique polynôme irréductible de degré 2 sur F₂, il est primitif, et c'est le polynôme cyclotomique d'indice trois :

${\displaystyle \Phi _{3,F_{2}}(X)=X^{2}+X+1.}$

Les racines des polynômes de degré 3 irréductibles sur F₂ sont les éléments de F_2³ = F₈ qui n'appartiennent pas à son unique sous-corps F₂. Ce sont donc les 6 générateurs du groupe multiplicatif F₈* à sept éléments. Par conséquent, il existe exactement 6/3 = 2 polynômes irréductibles de degré 3 sur F₂, ils sont primitifs, et leur produit est le polynôme cyclotomique d'indice sept. Ce sont donc les deux facteurs de :

${\displaystyle \Phi _{7,F_{2}}(X)=X^{6}+X^{5}+X^{4}+X^{3}+X^{2}+X+1=(X^{3}+X+1)(X^{3}+X^{2}+1).}$

Les racines des polynômes de degré 4 irréductibles sur F₂ sont les éléments de F_2⁴ = F₁₆ qui n'appartiennent pas au sous-corps intermédiaire F₄. Ce sont donc, dans le groupe multiplicatif F₁₆* à quinze éléments, les 12 dont le cube n'est pas 1. Par conséquent, il existe exactement 12/4 = 3 polynômes irréductibles de degré 4 sur F₂. Parmi leurs 12 racines, 8 sont d'ordre quinze (i.e. sont des générateurs du groupe) car φ(15) = 8, donc parmi ces trois polynômes, deux seulement sont primitifs et leur produit est le polynôme cyclotomique d'indice quinze. Ce sont donc les deux facteurs de :

${\displaystyle \Phi _{15,F_{2}}(X)=X^{8}+X^{7}+X^{5}+X^{4}+X^{3}+X+1=(X^{4}+X+1)(X^{4}+X^{3}+1).}$

Les 4 racines restantes sont d'ordre cinq, donc le polynôme irréductible de degré 4 non primitif est le polynôme cyclotomique d'indice cinq :

${\displaystyle \Phi _{5,F_{2}}(X)=X^{4}+X^{3}+X^{2}+X+1.}$

Caractéristique trois

Il existe sur F₃ trois polynômes unitaires de degré un, dont deux sont les polynômes cyclotomiques d'indices un et deux :

${\displaystyle X,\quad \Phi _{1,F_{3}}(X)=X-1\quad {\text{et}}\quad \Phi _{2,F_{3}}(X)=X+1.}$

L'extension d'ordre neuf contient six éléments hors du corps premier ; elle est de dimension deux, il existe donc exactement trois polynômes irréductibles. Le groupe multiplicatif est d'ordre huit et contient quatre éléments générateurs. Deux des polynômes irréductibles sont primitifs, le dernier est le polynôme cyclotomique d'ordre quatre.

${\displaystyle \Phi _{8,F_{3}}(X)=(X^{2}+X-1)(X^{2}-X-1)\quad {\text{et}}\quad \Phi _{4,F_{3}}(X)=X^{2}+1}$

L'extension d'ordre vingt-sept contient un unique sous-corps : le corps premier. Il existe donc 24 éléments hors de tout sous-corps et 24/3 = 8 polynômes irréductibles de degré 3. Le groupe multiplicatif contient vingt-six éléments dont 12 générateurs. Par conséquent, parmi les huit polynômes irréductibles de degré 3, 12/3=4 sont primitifs et ce sont les quatre facteurs de :

${\displaystyle \Phi _{26,F_{3}}(X)=(X^{3}-X+1)(X^{3}+X^{2}-X+1)(X^{3}-X^{2}+1)(X^{3}-X^{2}+X+1).}$

Les quatre polynômes irréductibles de degré 3 non primitifs sont polynômes minimaux des 12 éléments d'ordre treize du groupe multiplicatif. Ce sont donc les 12/3 = 4 facteurs de :

${\displaystyle \Phi _{13,F_{3}}=(X^{3}-X-1)(X^{3}+X^{2}+X-1)(X^{3}+X^{2}-1)(X^{3}-X^{2}-X-1).}$

Congruences et imaginaires de Galois

L'étude des corps finis premiers est traité systématiquement, sous forme de congruences, par Gauss dans ses Disquisitiones arithmeticae parues en 1801, mais beaucoup de ces propriétés avaient déjà été établies par entre autres Fermat, Euler, Lagrange et Legendre^[7].

En 1830, Évariste Galois publie^[28] ce qui est considéré comme l'article fondateur de la théorie générale des corps finis^[7]. Galois, qui déclare s'inspirer des travaux de Gauss sur les congruences entières, traite de congruences polynomiales, pour un polynôme irréductible à coefficients pris eux-mêmes modulo un nombre premier p. Plus précisément Galois introduit une racine imaginaire d'une congruence P(x) = 0 modulo un nombre premier p, où P est un polynôme irréductible modulo p. Il note i cette racine et travaille sur les expressions :

Retraduit en termes modernes, Galois montre que ces expressions forment un corps de cardinalité pⁿ, et que le groupe multiplicatif est cyclique (Kleiner 1999, I, p. 683). Il remarque également qu'un polynôme irréductible qui a une racine dans ce corps, a toutes ses racines dans celui-ci, c'est-à-dire qu'il s'agit d'une extension normale de son sous-corps premier (Lidl et Niederreiter 1997, p. 75). Il utilise l'identité donnée par ce qui a été appelé depuis l'automorphisme de Frobenius (Van der Waerden 1985, p. 111). En 1846, Liouville, en même temps qu'il fait publier le fameux mémoire de Galois sur la résolution des équations polynomiales, fait republier cet article dans son Journal de mathématiques pures et appliquées.

Il s'avère qu'en fait Gauss a mené des travaux au moins aussi complets sur le même sujet trente ans auparavant, quand il préparait ses Disquisitiones arithmeticae (cf. Frei 2007). Plutôt que d'introduire une racine imaginaire comme Galois, il travaille directement sur des polynômes, avec une double congruence, modulo p premier pour les coefficients, et modulo un polynôme irréductible (mais il mentionne que l'introduction de racines simplifierait la présentation). Il prépare un chapitre sur le sujet, qu'il met en attente pour une seconde partie qui ne paraîtra jamais de son vivant. Ce travail restera inconnu jusqu'à la parution posthume de l'édition de ses œuvres en 1863^[29]. C'est donc l'article de Galois qui est à l'origine des développements du XIX^e siècle sur les corps finis. Ainsi Serret^[30] donne une démonstration de l'existence d'un polynôme irréductible pour tout degré n et modulo tout nombre premier p, en termes modernes l'existence d'un corps fini de cardinal pⁿ (à cause de l'utilisation des imaginaires de Galois, la rigueur de celle-ci sera contestée par Dickson — cf. Dickson, p. 240). Il faut cependant mentionner également deux articles sur le sujet de Theodor Schönemann en 1845 et 1846, moins aboutis que ceux de Gauss et Galois, mais qui purent influencer Kronecker (Frei 2007, p. 72).

Théorie des corps

E. H. Moore montre en 1893 qu'un corps commutatif fini peut toujours se définir à la façon de Galois, en termes modernes, comme le corps de rupture d'un polynôme irréductible.

En 1893, le mathématicien américain E. H. Moore démontre qu'un corps (commutatif) fini est caractérisé par son cardinal^[7],[31] ; un corps fini est un ensemble de symboles, de cardinal fini s, muni des quatre opérations « sujettes aux identités ordinaires de l'algèbre abstraite^[32] », sans plus de précision. Moore montre qu'un tel corps est « la forme abstraite » d'un « champ de Galois » (en anglais : Galois field) de cardinal s = pⁿ défini à la façon de l'article de Galois, et du livre de Serret cités ci-dessus. La première présentation moderne de la théorie des corps finis est due à son ancien étudiant L. E. Dickson en 1901^[33],[7]. Joseph Wedderburn, qui séjourne à l'université de Chicago en 1904-1905, y travaille en étroite collaboration avec Dickson^[34]. Il démontre en 1905 qu'il n'existe pas de corps fini non commutatif. La structure des corps finis est entièrement élucidée.

Parallèlement, Heinrich Weber donne une première approche vraiment axiomatique de la théorie des corps (commutatifs) dans un article de 1893^[35]. Il souhaite ainsi unifier des notions apparues précédemment dans différents champs mathématiques, dont ce que nous appelons maintenant les corps finis (Kleiner 1999, II, p. 860). Le terme de corps (en allemand : Körper) est lui-même repris de Richard Dedekind^[36], qui l'avait introduit pour les sous-corps des réels ou des complexes, définis comme des sous-ensembles stables par les quatre opérations usuelles^[37]. Le traitement moderne de la théorie des corps commutatifs (avec les corps finis comme cas particuliers), fondé sur la définition axiomatique actuelle, est développé par Ernst Steinitz en 1910 dans un mémoire célèbre^[38].

Applications théoriques

Les corps finis sont, en particulier, utilisés en arithmétique, au fondement par exemple de l'arithmétique modulaire, laquelle a permis à Gauss de démontrer^[39] la loi de réciprocité quadratique. La structure de corps intervient notamment dans la résolution d'équations diophantiennes (voir section #Applications). Le petit théorème de Fermat est un exemple archétypal.

Artin utilise le fait qu'un contexte naturel des lois de réciprocité est celui des corps finis. C'est l'un des outils qui lui permettent de résoudre le neuvième problème de Hilbert. Il initie l'analyse de l'équivalent de la fonction zêta de Riemann sur les corps finis. La géométrie arithmétique se généralise sur des structures finies. Cette approche est particulièrement active durant la seconde moitié du XX^e siècle. André Weil généralise la démarche aux courbes algébriques et Pierre Deligne aux variétés algébriques. Les conjectures de Weil sur les variétés sur des corps finis, énoncées en 1940 par André Weil, font partie des problèmes importants de cette époque. Démontrées en 1974, elles ouvrent la voie au théorème de Taniyama-Shimura démontré par Andrew Wiles et ayant pour conséquence le dernier théorème de Fermat, souvent cité dans les articles de vulgarisation.

Applications pratiques

Voyager 2 utilise le code Reed-Solomon fondé sur la théorie des corps finis pour communiquer.

Après la Seconde Guerre mondiale et pour les besoins des laboratoires Bell, Claude Shannon formalise la théorie de l'information comme une branche des mathématiques^[40], posant les problématiques de la sécurité^[41] et de la fiabilité des transmissions.

La cryptologie s'appuie sur la possibilité de générer rapidement de grands nombres premiers. La confidentialité d'un message est assurée par l'insurmontable difficulté technique actuelle de casser des entiers, c'est-à-dire d'effectuer un algorithme permettant de décomposer un nombre en facteurs premiers en un temps raisonnable. Une recherche active cherche à créer de nouveaux algorithmes allant en ce sens. Ainsi, Michael Rabin publie^[42] un test de primalité se fondant sur les propriétés du groupe multiplicatif des corps premiers.

La fiabilité traite de la capacité à transmettre sans erreur un message malgré des altérations dans la communication, elle est traitée par la théorie des codes correcteurs. En 1950, Richard Hamming travaille pour les laboratoires Bell avec Shannon sur ce sujet. Il utilise^[43] des espaces vectoriels de dimension finie sur des corps finis pour formaliser un cadre opérationnel à la théorie et trouver les premiers exemples de codes correcteurs optimaux. Cette approche donne naissance à la théorie des codes linéaires.

En 1960, Raj Chandra Bose et Dwijendra Kumar Ray-Chaudhuri montrent^[44] que des idéaux de l'anneau des polynômes sur les corps finis de caractéristique 2 sont particulièrement adaptés. La théorie est généralisée^[45] par Alexis Hocquenghem et donne naissance à la famille de codes BCH. Deux autres fondateurs de la théorie, Irving Reed et Gustave Solomon, enrichissent la méthode^[46] et créent des codes à même de résister à de grosses altérations, les codes de Reed-Solomon. Les applications les plus connues sont probablement le système de communication de certaines sondes de la NASA comme Voyager ou les disques compacts. Durant les années 1970, les résultats d'arithmétique avancés sur les courbes elliptiques des corps finis trouvent leur application^[47] avec, par exemple, les codes de Goppa.

Équation diophantienne

Richard Dedekind.

Une équation diophantienne est une équation à coefficients entiers où des solutions entières sont recherchées. Pierre de Fermat s'est longuement penché sur des équations de cette nature.

Le petit théorème de Fermat stipule que, si p est premier, alors tout entier à la puissance p est congru modulo p à cet entier. Dans le contexte des corps finis, cela revient à indiquer que les points fixes de l'automorphisme de Frobenius sont les éléments du corps premier, ou que le groupe multiplicatif de ce dernier est cyclique d'ordre p – 1.

Fermat remarque que les seuls nombres premiers, somme de deux carrés, sont ceux dont la division par quatre donne un pour reste. Il remarque en effet que:

${\displaystyle 5=1^{2}+2^{2},\quad 13=2^{2}+3^{2},\quad 17=1^{2}+4^{2},\quad 29=2^{2}+5^{2},\quad 37=1^{2}+6^{2},\quad 41=4^{2}+5^{2}.}$

Il propose l'équation a² + b² = p avec p premier dans une lettre écrite à Marin Mersenne, datée du 25 décembre 1640.

Dedekind propose une démonstration^[48] dont la première partie consiste à étudier l'équation sur le corps F_p. Il utilise les propriétés du groupe multiplicatif et celles des polynômes à coefficients dans un corps. L'équation devient a² + b² = 0. Si b est égal à 0 alors a l'est aussi et la solution est triviale. Dans le cas contraire. Il est possible de diviser par b car la structure sous-jacente est celle d'un corps, l'équation devient alors X² + 1 = 0. En multipliant le polynôme précédent par X² – 1, il obtient l'équation X⁴ – 1 = 0. Les propriétés du groupe multiplicatif donnent une condition nécessaire et suffisante sur p : il doit être congru à 1 modulo 4. La fin de la démonstration n'utilise pas les corps finis ; elle est donnée dans l'article associé.

Cette méthode, consistant à réduire l'équation dans le corps premier est fréquente. Le corps possède une structure plus forte et l'on dispose de nombreux théorèmes pour conclure.

Code correcteur

Les codes correcteurs ont leur source dans un problème très concret lié à la transmission de données : dans certains cas, une transmission de données se fait en utilisant une voie de communication qui n'est pas entièrement fiable ; autrement dit, les données, lorsqu'elles circulent sur cette voie, sont susceptibles d'être altérées. L'objectif d'un code correcteur est l'apport d'une redondance de l'information de telle manière que l'erreur puisse être détectée et même corrigée.

Un message est une suite finie de lettres, qui dans le cas d'un code linéaire sont considérées comme des éléments d'un corps fini. Un message m apparaît comme un élément d'un espace vectoriel E sur un corps fini de dimension k. L'apport de la redondance est le résultat d'une application linéaire injective φ de E dans un espace F appelé code et de dimension n supérieure à k. Le mot du code transmis est l'élément φ(m). L'intérêt de transmettre φ(m) à la place de m est illustré par la figure suivante :

Illustration d'un code non correcteur et d'un code correcteur.

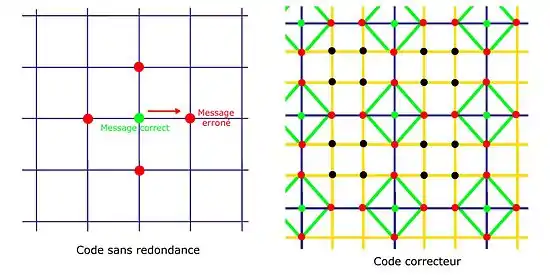
Si le message m est transmis, et si la transmission l'altère, alors le message reçu est erroné (comme illustré sur la figure de gauche) et le récepteur ne dispose d'aucun moyen pour repérer ou corriger l'erreur. Si l'application φ est astucieusement choisie, chaque point du code diffère des autres points du code par au moins d coordonnées. Cette situation est illustrée sur la figure de droite. Les points du code sont figurés en vert, la modification d'une coordonnée est symbolisée par un segment du quadrillage. On remarque sur la figure que les points du code diffèrent tous par au moins d = 3 coordonnées. Si, par exemple, l'altération porte sur une unique coordonnée, la transmission correspond à un point rouge. Le récepteur peut alors corriger l'erreur, car il n'existe qu'un seul point du code (en vert) à une distance égale à 1 du message reçu.

Illustration d'un code parfait.

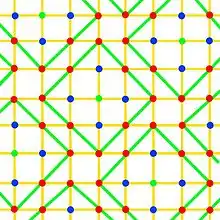
L'application qui, à deux points de F, associe le nombre de coordonnées distinctes est une distance au sens mathématique, appelée distance de Hamming. Si la distance de Hamming minimale entre deux points du code est égale à d, alors le code est à même de corriger t altérations où t est le plus grand entier strictement plus petit que d/2. Sur la figure ci-dessus, on remarque des points noirs. Ils correspondent à des redondances inutiles. Ils sont en effet à une distance égale à 2 des points du code, or une telle distance n'est pas traitable dans le cas de la figure.

L'ensemble des points corrigeables est donné par la réunion de toutes les boules de centre un point du code et de rayon t. La configuration idéale est celle où ces boules forment une partition de F. Il n'existe alors aucune redondance inutile. Cette situation est illustrée par la figure de droite. Les points du code sont illustrés en vert, la distance minimale d est égale à 5. Les boules de centre les points du code et de rayon 2 forment une partition de F. Les points à distance 1 du code sont illustrés en bleu, ceux à distance 2 en rouge. Tout message contenant au plus deux altérations peut être corrigé. Un tel code est dit parfait.

La théorie des corps finis permet de construire des codes parfaits. L'espace F est muni de la structure d'anneau F_d[X]/P(X) où P(X) = Xⁿ – 1 avec n = d^a – 1 et a est un entier strictement positif. F correspond à l'ensemble des polynômes prenant des valeurs distinctes sur le corps F_n+1. Si φ(E) est l'idéal engendré par le polynôme G(X) à coefficients dans F_d ayant pour racines α, α², ..., α^d–1, alors le code est de distance minimale d. G(X) est le produit de polynômes cyclotomiques. Le code BCH ou le code de Reed-Solomon utilise cette technique pour construire des codes parfaits. Si k est l'entier tel que n – k est égal au degré de G(X), alors l'application φ associe au message M(X) le polynôme M(X)X^k – R(X) où R(X) est le reste de la division euclidienne de M(X).X^k par G(X). Les détails et démonstrations sont donnés dans l'article code cyclique.

Géométrie arithmétique

Mathématiques

• Michel Demazure, Cours d'algèbre. Primalité Divisibilité. Codes, 2008 [détail de l’édition]
• Daniel Perrin, Cours d'algèbre, 1981 [détail des éditions]
• Pierre Samuel, Théorie algébrique des nombres [détail de l’édition]
• Jean-Pierre Serre, Cours d'arithmétique, 1970 [détail des éditions]
• André Warusfel, Structures algébriques finies, Hachette, 1971
• (en) Rudolf Lidl et Harald Niederreiter, Finite Fields, CUP, 1997, 2^e éd., 755 p. (ISBN 978-0-521-39231-0, présentation en ligne), contient également des notes historiques en fins de chapitres.

Histoire des mathématiques

• (en) Leonard Eugene Dickson, History of the Theory of Numbers [détail des éditions] livre 1, en particulier le chapitre 8 Higher congruences et p. 233 Theory of higher congruences, Galois imaginaries.
• (en) Günther Frei (de), The Unpublished Section Eight : On the Way to Function Fields over a Finite Field, p. 159-198, in (en) Catherine Goldstein, Norbert Schappacher et Joachim Schwermer (de) (éds.), The Shaping of Arithmetic after C. F. Gauss's Disquisitiones arithmeticae [détail des éditions]
• (en) Israel Kleiner, « Field Theory: From Equations to Axiomatization — Part I », Amer. Math. Monthly, vol. 106, n^o 7,‎ 1999, p. 677-684 (JSTOR 2589500) et (en) Israel Kleiner, « — Part II », ibid., n^o 9,‎ 1999b, p. 859-863 (JSTOR 2589621), republiés dans (en) Israel Kleiner, A History of Abstract Algebra, Boston, Birkhäuser, 2007, 168 p. (ISBN 978-0-8176-4684-4, lire en ligne), « History of Field Theory », p. 63-78
• (en) B. L. Van der Waerden, A History of Algebra, from Al-Khwarizmi to Emmy Noether, Springer-Verlag, 1985, 271 p. (ISBN 978-3-540-13610-1)

Articles connexes

• Factorisation des polynômes à coefficients dans les corps finis
• Algorithme de Berlekamp
• Algorithme de Cantor-Zassenhaus
• Corps quasi-algébriquement clos
• Théorème d'Artin-Zorn (en)
• Corps à un élément
• Corps quasi-fini

Liens externes

• Notices d'autorité :

  • BnF (données)
  • LCCN
  • Israël
• Notice dans un dictionnaire ou une encyclopédie généraliste :

  • Britannica
• Codes géométriques algébriques et arithmétique sur les corps finis, journées X-UPS 1993, Centre de mathématiques de l'École polytechnique
• David Madore, « Corps finis, cours » (version du 19 avril 2009 sur Internet Archive) et « TD »
• David Madore, « Factorisation de polynômes sur les corps finis » (version du 9 mai 2007 sur Internet Archive)