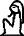| Naissance |
Vers 625-620 avant J.-C. Milet |
|---|---|
| Décès |
Vers 548-545 avant J.-C. Milet |
| École/tradition |
École milésienne |
| Principaux intérêts | |
| Idées remarquables |
Eau comme substance première, théorème de Thalès |
| Influencé par |
Philosophie égyptienne, Homère |
| A influencé |
École milésienne, Pythagore |
| Père |
Examyas (d) |
| Mère |
Cleobulina (d) |
Thalès de Milet, appelé communément Thalès (en grec ancien : Θαλῆς ὁ Μιλήσιος / Thalễs ho Milếsios), est un philosophe et savant grec, né à Milet vers 625-620 av. J.-C. et mort vers 548-545 av. J.-C. dans cette même ville[1],[2],[3].
C'est l'un des Sept sages de la Grèce antique et le fondateur présumé de l'école milésienne. Philosophe de la nature, il passe pour avoir effectué un séjour en Égypte, où il aurait été initié aux sciences égyptienne et babylonienne. On lui attribue de nombreux exploits, comme le calcul de la hauteur de la grande pyramide ou la prédiction d'une éclipse, ainsi que le théorème de Thalès. Il fut l'auteur de nombreuses recherches mathématiques, notamment en géométrie.
Personnage légendaire, qui semble n'avoir rien écrit, sa méthode d'analyse du réel en fait l'une des figures majeures du raisonnement scientifique. Il sut s'écarter des discours explicatifs délivrés par la mythologie pour privilégier une approche caractérisée par l'observation et la démonstration.
Biographie
Thalès de Milet est considéré comme le premier philosophe de la nature (φυσικὸς φιλόσοφος), scientifique et mathématicien grec. Il est d'abord commerçant et ingénieur[4] mais aussi homme politique. Son père est Examyes, sa mère Cléobuline[5]. Selon Hérodote[6], les ancêtres de Thalès étaient originaires de Phénicie.
Origine et dates
Il est difficile de situer le personnage dans le temps, même en tenant compte de la date de l'éclipse solaire qu'il est supposé avoir prédite, vraisemblablement vers 585 av. J.-C.[5]. Hérodote explique dans quelles circonstances eut lieu cette éclipse :
« Pendant cinq années la guerre dura entre les Mèdes et les Lydiens ; ils eurent alternativement de fréquents avantages, et la sixième année, il y eut une espèce de combat nocturne : car, après une fortune égale de part et d'autre, s'étant livré bataille, le jour se changea tout à coup en nuit, pendant que les deux armées en étaient aux mains. Thalès de Milet avait prédit aux Ioniens ce changement, et il en avait fixé le temps en l'année où il s'opéra. Les Lydiens et les Mèdes, voyant que la nuit avait pris la place du jour, cessèrent le combat, et n'en furent que plus empressés à faire la paix[notes 1]. »
Diogène Laërce, citant Apollodoros, a rapporté quant à lui qu'il serait né pendant la 35e olympiade (vers 640 av. J.-C.) et mort à 78 ans (vers 562 av. J.-C.) ; il cite aussi Sosicrate qui le fait vivre 90 ans, c'est-à-dire jusqu'au début de la 58e olympiade (vers 550)[notes 2]. La vie de Thalès a manifestement été idéalisée, et ce que nous connaissons de ce penseur, comme pour les autres présocratiques, nous renseigne surtout sur le type commun du sage en Grèce. Rapportant les dires d'Hérodote, Diogène raconte que Thalès serait le fils d'Examios, un marchand, et de Cléobuline, tous deux d'origine phénicienne (même s'il est plus que probable qu'il ait bien été un Grec[7]) :
« Thalès, aux dires d’Hérodote, de Douris et de Démocrite, était fils d’Examios et de Cléobuline, et membre de la famille des Thélides, Phéniciens descendant en droite ligne d’Agénor et de Cadmos, s’il faut en croire Platon[notes 3]. »
Une légende raconte en effet qu'il descend de la famille des Thélides, des rois mythiques de Phénicie de la lignée d'Agénor et de Cadmos. Plusieurs autres sources affirment pourtant qu'il était peut-être d'origine béotienne ou phénicienne et probablement contemporain de Solon et de Crésus et qu'il se serait installé à Milet en compagnie de son ami Neileôs. Il n'est donc pas sûr que Thalès soit Milésien, quoiqu'une tradition courante fasse de lui un descendant d'une famille aisée de Milet. Cependant, il faut insister sur le fait que les sources les plus fiables et complètes proviennent de Diogène Laërce et d'Hérodote. Il semble que Thalès ait commencé sa vie comme simple commerçant puis qu'il se soit orienté vers une carrière politique et économique, après un séjour en Égypte[8]. Selon ce que rapporte Diogène Laërce[9], Platon serait peut-être né à Égine, dans la maison de Phidiadas — ce Phidiadas est fils de Thalès.
Séjour en Égypte
Aétius et Proclos, ainsi que d'autres auteurs antiques, rapportent que Thalès, alors jeune, a fait un séjour en Égypte, puis qu'il s'est installé par la suite à Milet[10]. Cette ville entretenait d'ailleurs des relations étroites avec la colonie de Naucratis, en Égypte, ce qui corrobore cette thèse. Selon Jean-Paul Dumont, si Thalès n'eut pas de maître, c'est en Égypte qu'il put acquérir ses connaissances, grâce à l'enseignement des prêtres[11]. L'étude des textes évoquant cette période laisse entendre que Thalès s'y rendit alors très jeune, et qu'il y passa par conséquent son enfance[12].
Il y aurait rapporté la science de la géométrie et, en effet, nombre de ses réalisations et exploits (notamment sa théorie sur les crues du Nil) s'insèrent dans le cadre de ce pays.
Il fréquenta, selon Michel Soutif, la bibliothèque et l'observatoire fondés par Teglath-Phalasar III qui régna sur l'Assyrie de 744 à 723[13].
Toutefois, il est possible que le séjour égyptien ait été ajouté à sa légende, du fait qu'il était l'un des Sept Sages, comme Solon[14]. Pour D. R. Dicks, le séjour en Égypte serait un mythe, ainsi que les attributions de découvertes en mathématiques à Thalès par des biographes qui vécurent des siècles après sa mort[15].
Carrière politique
Doué d'une « faculté d'adaptation intellectuelle » hors du commun, Thalès a aussi été un homme d'État rapporte Hérodote[16]. En ce qui concerne sa carrière politique, Diogène Laërce dit : « Il paraît aussi avoir été un éminent conseiller politique. Ainsi il marqua son opposition, quand Crésus envoya une ambassade proposer aux Milésiens de s'engager à ses côtés ; étant donné ensuite la victoire de Cyrus, ce refus assura la survie de la Cité. » Thalès le scientifique ne doit donc pas occulter un autre Thalès, habile en affaires et prompt à dénigrer ses propres découvertes et sa fortune acquise. Il connut en effet d'abord sa renommée comme conseiller militaire et comme ingénieur. Durant la guerre entre les Perses et les Lydiens, il aurait détourné le cours du fleuve Halys pour faire passer l'armée de Crésus selon Hérodote, légende qui semble très vraisemblable[16] :
« Cyrus tenait donc prisonnier Astyages, son aïeul maternel, qu'il avait détrôné pour les raisons que j'exposerai dans la suite de cette histoire. Crésus, irrité à ce sujet contre Cyrus, avait envoyé consulter les oracles pour savoir s'il devait faire la guerre aux Perses. Il lui était venu de Delphes une réponse ambiguë, qu'il croyait favorable, et là dessus il s'était déterminé à entrer sur les terres des Perses. Quand il fut arrivé sur les bords de l'Halys, il le fit, à ce que je crois, passer à son armée sur les ponts qu'on y voit à présent ; mais, s'il faut en croire la plupart des Grecs, Thalès de Milet lui en ouvrit le passage. Crésus, disent-ils, étant embarrassé pour faire traverser l'Halys à son armée, parce que les ponts qui sont maintenant sur cette rivière n'existaient point encore en ce temps-là, Thalès, qui était alors au camp, fit passer à la droite de l'armée le fleuve, qui coulait à la gauche. Voici de quelle manière il s'y prit. Il fit creuser, en commençant au-dessus du camp, un canal profond en forme de croissant, afin que l'armée pût l'avoir à dos dans la position où elle était. Le fleuve, ayant été détourné de l'ancien canal dans le nouveau, longea derechef l'armée, et rentra au-dessous de son ancien lit. Il ne fut pas plutôt partagé en deux bras, qu'il devint également guéable dans l'un et dans l'autre. Quelques-uns disent même que l'ancien canal fut mis entièrement à sec ; mais je ne puis approuver ce sentiment. Comment en effet Crésus et les Lydiens auraient-ils pu traverser le fleuve à leur retour[notes 4] ? »
Il apparaît alors comme le conseiller de l'alliance entre Lydiens et Ioniens, contre le royaume mède. Cette réputation, après la chute de Crésus, lui permit de convaincre les cités-États (ou polis) d'Ionie de se regrouper en fédération pan-ionienne, selon Hérodote[8] :
« Quoique accablés de maux, les Ioniens ne s'en assemblaient pas moins au Panionion. Bias de Priène leur donna, comme je l'ai appris, un conseil très avantageux, qui les eût rendus les plus heureux de tous les Grecs, s'ils eussent voulu le suivre. Il les exhorta à s'embarquer tous ensemble sur une même flotte, à se rendre en Sardaigne, et à y fonder une seule ville pour tous les Ioniens. Il leur fit voir que, par ce moyen, ils sortiraient d'esclavage, qu'ils s'enrichiraient, et qu'habitant la plus grande de toutes les îles, les autres tomberaient en leur puissance; au lieu que, s'ils restaient en Ionie, il ne voyait pour eux aucune espérance de recouvrer leur liberté. Tel fut le conseil que donna Bias aux Ioniens, après qu'ils eurent été réduits en esclavage ; mais, avant que leur pays eût été subjugué, Thalès de Milet, dont les ancêtres étaient originaires de Phénicie, leur en donna aussi un qui était excellent. Ce fut d'établir à Téos, au centre de l'Ionie, un conseil général pour toute la nation, sans préjudicier au gouvernement des autres villes, qui n'en auraient pas moins suivi leurs usages particuliers que si elles eussent été autant de cantons différents[notes 5]. »
Cependant, il semble que Thalès ait décidé de traiter séparément avec Cyrus, peut-être pour des raisons commerciales[8].
Activités scientifiques
Grâce à son séjour en Égypte, Thalès put mettre en œuvre ses connaissances en mathématiques, particulièrement en géométrie, domaines dans lesquels il fit quelques découvertes fondamentales[notes 6], comme déterminer qu'un cercle est partagé en deux parties égales par tout diamètre ou que les angles à la base d'un triangle isocèle sont égaux (voir infra). Ses découvertes astronomiques permirent d'aider à la navigation en haute mer en repérant certaines étoiles ou en déterminant les éphémérides (voir infra). Il est probable que Thalès ait consigné ses découvertes par écrit afin d'en diffuser l'utilité, même s'il ne demeure à ce jour aucun texte de sa main[17].
Selon Proclos, dans ses Commentaires sur le premier livre des éléments d’Euclide (65, 3), Thalès usait d’approches variées, « tantôt plus universelles, tantôt plus empiriques ». « Les mathématiques, au sens propre du mot, n'ont commencé à exister que quelque temps après Thalès » note John Burnet[18].
Jean Voilquin, dans son ouvrage sur les présocratiques, crédite Thalès d'avoir cherché à « remplacer l'explication mythique » des phénomènes « par une explication physique », et il est en cela « un des précurseurs de la science grecque »[19].
Mort et modèle de sagesse

Passionné de gymnastique, Thalès passe pour avoir été retrouvé dans les gradins, mort par déshydratation lors d'une compétition à laquelle il assistait, selon Diogène Laërce : « Thalès le Sage mourut en assistant à une rencontre sportive, du fait de la faim, de la soif, et de la faiblesse de l'âge ». Ce dernier aurait écrit une épigramme à ce propos, rapportée au premier livre de son ouvrage Épigrammes (Pammétros) :
Tandis qu'il contemplait une lutte sportive,
Zeus Solaire, tu as, hors du stade, ravi
Thalès dont la sapience avait fait le renom.
Je te loue de l'avoir rappelé près de toi,
Car il était très vieux, et depuis cette terre,
La force lui manquait pour observer les astres.
Selon Apollodore, sa mort survint lors de la chute de Sardes[5], lors des 58e Olympiades, à l'âge de 78 ans ou, 90 ans selon Sosicrate, rapporte Diogène Laërce[notes 7]. Selon Diogène Laërce une épitaphe inscrite sur la tombe de Thalès rappelle qu'il fut un grand homme :
« Ce tombeau, certes est bien petit – mais la renommée de l’homme est allée au ciel. C’est celui de Thalès le très sage[notes 8]. »
Le portrait de Thalès relève d’une catégorie cultuelle, celle du Sage. Il est en effet le premier du genre et apparaît dans toutes les listes de sages connues notamment chez Apulée (Florides, 18) ou chez Platon (Protagoras, 343 a)[20]. Sa renommée se fonde essentiellement sur certaines anecdotes comme l’épisode du puits rapporté par Platon (et repris par Jean de La Fontaine dans ses Fables, dans la 13e, intitulée L’Astrologue qui se laisse tomber dans un puits au Livre II) :
« Socrate : L’exemple de Thalès te le fera comprendre, Théodore. Il observait les astres et, comme il avait les yeux au ciel, il tomba dans un puits. Une servante de Thrace, fine et spirituelle, le railla, dit-on, en disant qu’il s’évertuait à savoir ce qui se passait dans le ciel, et qu’il ne prenait pas garde à ce qui était devant lui et à ses pieds[notes 9]. »
Thalès est devenu pour les Grecs un « symbole d'ingéniosité », à tel point qu'un personnage du théâtre d'Aristophane, dans sa pièce Les Oiseaux, dit, en parlant de l'urbaniste Méton d'Athènes, qu'il pourrait être « un Thalès ». Platon quant à lui le compare à Anacharsis dans sa République[16]. Selon la tradition, c'est Anaximène qui a continué les travaux de Thalès[21].
Diogène Laërce raconte que Thalès fut nommé, après sa mort, « Sage » par l'archonte d'Athènes Damasias l'un des « Sept sages »[22]. Selon Karin Mackowiak, « la vie de Thalès peut être issue d’une mise en forme mythique analogue à celle qui concerne la vie de Pythagore »[23]. Par la suite, Aristote (Métaphysique, I, 3, 983 b) en fait un connaisseur des lois du monde et « le place au plus haut degré de la sagesse en qualité d’initiateur de la philosophie spéculative et de moraliste »[20].
Théories
Cosmologie
L'eau, principe supérieur
| La pensée de Thalès : | |
|
ἐκ τοῦ ὕδατός φησι συνεστάναι πάντα (« L'eau est la cause matérielle de toutes choses ») |

La philosophie de la nature de Thalès, connue surtout grâce à Aristote[24] — qui la tient lui-même de sources intermédiaires[25] — fait de l'eau le principe matériel (αρχή : arche) explicatif de l'univers, d'où procèdent les autres éléments : air, feu et terre. Accordant une vitalité à cette matière unique et universelle, il estime que l'eau est le principe de toutes choses. Ainsi, l’air, le feu et la terre ne sont que différentes formes prises par l’eau : la terre de l’eau condensée, l’air de l’eau raréfiée et le feu nourri par l’air ; tout se résout en eau. Aristote résume ainsi la pensée de Thalès et la prépondérance donnée à l'eau au sein de celle-ci[26] :
« Thalès, le fondateur de cette manière de philosopher, prend l'eau pour principe, et voilà pourquoi il a prétendu que la terre reposait sur l'eau, amené probablement à cette opinion parce qu'il avait observé que l'humide est l'aliment de tous les êtres, et que la chaleur elle-même vient de l'humide et en vit ; or, ce dont viennent les choses est leur principe. C'est de là qu'il tira sa doctrine, et aussi de ce que les germes de toutes choses sont de leur nature humides, et que l'eau est le principe des choses humides. Plusieurs pensent que dès la plus haute antiquité, bien avant notre époque, les premiers théologiens ont eu la même opinion sur la nature : car ils avaient fait l'Océan et Téthys auteurs de tous les phénomènes de ce monde, et ils montrent les dieux jurant par l'eau que les poètes appellent le Styx. En effet, ce qu'il y a de plus ancien est ce qu'il y a de plus saint ; et ce qu'il y a de plus saint, c'est le serment. Y a-t-il réellement un système physique dans cette vieille et antique opinion ? C'est ce dont on pourrait douter. Mais pour Thalès on dit que telle fut sa doctrine[notes 10]. »
La raison de ce choix pour l'eau provient semble-t-il de l'importance de celle-ci dans la croissance et la nutrition des choses vivantes, de son rôle central dans le quotidien des Milésiens et des observations qu'on prétend qu'il a faites en Égypte quant à l'importance du Nil et des autres fleuves qui faisaient l'objet de cultes[27]. Cependant, l'originalité de Thalès est de faire de cette explication mythologique un principe de connaissance physique mais aussi métaphysique ; en effet, l'unité de l'élément eau est aussi l'unité du monde comme le résume le doxographe Aetius : « Thalès et son école : le monde est un ». L'eau comme principe universel d'explication n'est présent que dans la pensée de Thalès ; « on n'en trouve pas d'écho dans le monde grec », si bien qu'il s'agit certainement d'une conception rapportée des pays à l'Est de la Grèce[28].
Entreprise de rationalisation

La thèse de Thalès est une innovation d'importance car elle suppose l'affirmation de vérités, non à partir de quelques objets singuliers, comme c'était le cas avant lui pour les Égyptiens ou les Babyloniens, mais pour une infinité d'objets contenus dans le monde et pour le monde lui-même. Il énonce donc des vérités concernant une classe entière d'êtres. Ainsi, selon l'helléniste allemand Eduard Zeller, au XIXe siècle, l'apport majeur de Thalès est d'avoir généralisé et conceptualisé ses observations, d'être parvenu au concept de l'« Un » sans se perdre dans l'accumulation d'observations disparates . On attribue parfois à Thalès une conception de l'univers assez séduisante : celui-ci serait un genre de bulle d'air hémisphérique formée par la concavité du ciel et la surface plane de la Terre, qui flotte elle-même sur l'eau. Le mouvement de la Terre sur l'eau expliquerait les tremblements de terre rapporte Sénèque[28],[notes 11]. Thalès « place donc l'eau (ὕδωρ) en tant que principe, sans contexte mythique, à l'origine des choses. » Nietzsche, dans La naissance de la philosophie à l'époque de la tragédie grecque, a dit qu'à travers l'eau, Thalès a su discerner l'unité de l'être[29], c'est-à-dire un principe explicatif rationnel.
Toutefois, la thèse de Thalès n'étant connue que par l'intermédiaire d'Aristote et des péripatéticiens, le risque d'une déformation est non négligeable. Il est possible que Thalès n'ait pas pensé que tout était explicable par l'eau mais qu'il en fasse seulement l'élément originel[21]. Il a su utiliser une analogie, le concept d'« archè », pour expliquer l'essence de chaque être. Ce discours pré-scientifique a permis une rationalisation du monde. Thalès est, selon Leopoldo Iribarren, « le premier penseur archaïque à vaincre les résistances sémantiques posées par le discours mythique aux tentatives de régularisation du monde sous un principe explicatif unique ». L’affirmation de Thalès « opère la délimitation d’un horizon idéal des affirmations au-delà des situations énonciatives de la poésie inspirée »[30]. Au sein de l'histoire de la philosophie, Thalès reste donc « une figure de transition entre l’interprétation universalisante des grands mythes et l’argumentation d’une compréhension du monde »[31].
« Eudème, dans ses livres Sur l’astronomie raconte qu’Œnopide a trouvé le premier l’obliquité du zodiaque et reconnu l’existence de la grande année : d’après lui, Thalès a fait voir que les éclipses de soleil et les retours de cet astre aux solstices n’arrivent pas toujours après le même temps ; Anaximandre prétend que la terre est suspendue dans l’espace et se meut autour du centre du monde ; Anaximène a montré que la lune reçoit la lumière du soleil et de quelle manière elle s’éclipse. D’autres ont ajouté de nouvelles découvertes à celles-là : que les étoiles se meuvent autour de l’axe immobile qui passe par les pôles, que les planètes se meuvent autour de l’axe perpendiculaire au zodiaque ; et que l’axe des étoiles et celui des planètes s’écartent l’un de l’autre, du côté du pentadécagone, et par conséquent d’un angle de 24 degrés »[32].
Influence égyptienne et phénicienne
| L'eau primordiale (« Noun ») en hiéroglyphes. | |||||
| |||||
Theodor Gomperz énumère les influences possibles de la philosophie de Thalès. L'eau comme élément primitif dans sa cosmogonie est d'origine incertaine, peut-être phénicienne et égyptienne. La conception d'une terre flottante, comme un disque de bois reposant sur l'eau évoluant dans un univers rempli de matière primordiale, c'est-à-dire envisagé comme une masse liquide, s'accorde en effet, dans une certaine mesure, avec l'idée égyptienne de l'eau primordiale (« Noun »), surface divisée en deux masses séparées, selon Paul Tannery[33]. Selon Théophile Obenga, la conception de l'eau chez Thalès est en effet très proche de celle du Noun des Égyptiens, « matière-esprit destinée à l'évolution »[29].
Les anciens Babyloniens admettaient également l'idée d'un océan supérieur et d'un océan inférieur, montre Fritz Hommel[34]. Il existe aussi selon Gomperz des similitudes avec le livre de la Genèse (I, 7). La concordance entre la doctrine fondamentale de Thalès et celle de la secte judéo-chrétienne des Sampséens reste cependant à préciser selon lui[35]. La tendance actuelle est de considérer Thalès comme un simple intermédiaire entre étrangers et Grecs ; cette tendance a pourtant contre elle la façon dont la meilleure autorité, Eudème, parle des travaux géométriques de Thalès et du rapport dans lequel ils se trouvent avec la mathématique égyptienne conclut Theodor Gomperz[36].
Animisme et religion
Selon Diogène Laërce, Chérilos de Samos a soutenu que Thalès de Milet avait le premier proclamé l’immortalité de l’âme. Diogène rapporte également que Thalès pensait que toute chose avait une âme et que cette âme participait de tout l'univers, en conséquence de quoi il considérait que toutes les choses étaient remplies de dieux (c'est l'hylozoïsme). Cette dernière proposition lui permit de dire que l'âme est immortelle. L'assertion concernant la participation de l'âme au cosmos proviendrait de l'observation des propriétés magnétiques de certaines pierres et de l'ambre. Toutefois, il est possible qu'Hippias, puis Aristote, aient mal compris cette théorie. Aristote aurait notamment généralisé la thèse de Thalès au point de faire de l'âme la seule force motrice. Thalès semble, avec cette théorie, puiser aux sources de la pensée primitive pré-verbale[37]. En cela, il affirme l'unité de la matière[38].
Mathématiques
Thalès est la première personnalité des mathématiques ayant laissé la trace de son nom dans l'Histoire[39]. Il a formulé plusieurs propriétés géométriques qu'il tenait peut-être des Égyptiens et dont les premières traces de démonstration connues sont bien ultérieures[notes 12] mais, ce faisant, il pose les premiers jalons du raisonnement sur des figures idéales.
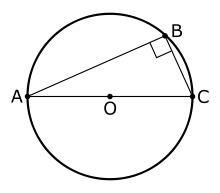
Théorème de Thalès
Deux théorèmes de géométrie très différents ont été appelés « théorème de Thalès » dans l'enseignement, à partir de la toute fin du XIXe siècle[40].
- Dans certains pays, à commencer par l'Allemagne, mais pas ou peu en France[40], le « théorème de Thalès » porte sur l'angle inscrit dans un demi-cercle : si un triangle est inscrit dans un cercle avec un côté du triangle pour diamètre du cercle, alors ce triangle est rectangle d'hypoténuse ce diamètre[41] - [42]. L'attribution à Thalès est tardive, elle repose sur un auteur du IIIe siècle apr. J.-C., Diogène Laërce, qui évoque également une autre paternité :
« Pamphila raconte, de son côté, qu’il [Thalès] avait appris la géométrie des Égyptiens ; que le premier il inscrivit dans le cercle un triangle rectangle, et qu’il immola un bœuf à cette occasion. Apollodore le calculateur et quelques autres mettent cela sur le compte de Pythagore[43]. »
Quoi qu'il en soit, pour une majorité d'historiens, la pratique des mathématiques de l'époque ne permettait pas à Thalès de fournir une démonstration logique comparable à celle que l'on trouve en Grèce deux ou trois siècles plus tard. Ses énoncés mathématiques et ceux de l'école Ionienne devaient plutôt relever de l'intuition empirique[44].
- En France et dans d'autres pays (comme l'Italie), le « théorème de Thalès » désigne un autre théorème, sur les rapports de longueurs dans un triangle coupé par une droite parallèle à l'un des côtés, ou une généralisation de ce résultat[40]. Le théorème, formulé dans un triangle quelconque, apparait effectivement, trois siècles après Thalès, dans le Livre VI (proposition 2) des Éléments d'Euclide. Sa démonstration repose alors sur la proportionnalité d'aires de triangles de même hauteur.
Ces deux dénominations apparaissent à une époque, la fin du XIXe siècle et le début du XXe siècle, où l'enseignement secondaire se développe. Toutes deux semblent avoir un sens plus didactique qu'historique : il s'agit d'abord de mettre en valeur un théorème considéré comme important à un certain niveau d'enseignement. Des traditions différentes de l'enseignement de la géométrie, en particulier entre la France et l'Allemagne, expliquent ces choix divergents[40].
La seconde dénomination renvoie à la mesure de la hauteur des pyramides d'Égypte par la mesure de leur ombre. Elle est rapportée par Pline l'Ancien, Plutarque et Diogène Laërce[45]. Pour Pline et pour Diogène Laërce, Thalès attend que son ombre soit égale à sa taille pour mesurer l'ombre de la pyramide[45]. Il en déduit alors de manière empirique donc, et non théorique, qu'il doit en être de même pour la pyramide[46]. Diogène Laërce écrit au IIIe siècle mais cite sa source, Hieronymus de Rhodes un disciple d'Aristote, qui est probablement également celle de Pline[45].

Plutarque donne une version romancée dans Le Banquet des Sept Sages (147a) qui, elle, fait bien intervenir des rapports de proportionnalité[47] :
« Ainsi, vous, Thalès, le roi d'Égypte vous admire beaucoup, et, entre autres choses, il a été, au-delà de ce qu'on peut dire, ravi de la manière dont vous avez mesuré la pyramide sans le moindre embarras et sans avoir eu besoin d'aucun instrument. Après avoir dressé votre bâton à l'extrémité de l'ombre que projetait la pyramide, vous construisîtes deux triangles par la tangence d'un rayon, et vous démontrâtes qu'il y avait la même proportion entre la hauteur du bâton et la hauteur de la pyramide qu'entre la longueur des deux ombres[48]. »
Pour Robert Baccou[49], « on peut interpréter l’étonnement du roi comme l’introduction d’une méthode entièrement nouvelle qui surpasse la science somme toute embryonnaire et empirique des Égyptiens »[50]. Cependant Maurice Caveing fait remarquer qu'« il est peu vraisemblable que le souverain d'un pays qui, plus de 1000 ans avant Thalès, connaissait le calcul du seq'd, ait ignoré comment mesurer la hauteur des pyramides »[45].
La version de Diogène Laërce et de Pline (celle où l'ombre de Thalès égale sa hauteur), qui est la plus simple mathématiquement, est donc très certainement celle d'origine[47]. La mesure de l'ombre pose tout de même une difficulté, d'une part l'ombre du sommet de la pyramide doit être à l'extérieur de la base de la pyramide, d'autre part la mesure doit partir du centre de la pyramide[51]. Elle peut être résolue facilement quand l'alignement du Soleil et du sommet de la pyramide est parallèle avec un côté de la base, ce qui, sachant aussi que l'ombre doit égaler la hauteur, arrive deux fois par an. Au moment où l'ombre d'un bâton égale sa hauteur, il suffit alors d'ajouter la longueur de l'ombre au sol avec la moitié de la longueur du côté de la pyramide pour obtenir la hauteur du bâtiment[51],[52].
Denis Guedj, développe et agrémente cette légende dans Le Théorème du Perroquet[53].
Autres propriétés
D'autres propriétés géométriques sont attribuées à Thalès par Proclus notamment, commentateur d'Euclide, dans son Commentaire sur le premier livre d'Euclide[42] :
- un cercle est partagé en deux parties égales par tout diamètre ;
- les angles à la base d'un triangle isocèle sont égaux ;
- les angles opposés par le sommet sont égaux lorsque deux droites se coupent ;
- deux triangles sont égaux s'ils ont deux angles et le côté compris égaux.
Astronomie
Découvertes
Thalès est considéré comme l'un des fondateurs de l’astronomie : il décrivit notamment la Petite Ourse et conseilla aux marins de s’en servir pour se guider, calcula la durée de l’année et des intervalles des solstices aux équinoxes, évalua le diamètre apparent du Soleil et les grandeurs relatives de cet astre et la Lune, sans doute en s'aidant d'un instrument tel qu'un gnomon ou un bâton vertical lui permettant de mesurer la portée de l'ombre du soleil[54]. L'intérêt de Thalès de Milet pour l'astronomie le poussa à faire de nombreuses observations sur les constellations. Il aurait été le premier à noter le voyage du soleil entre les deux tropiques. Il établit aussi que certaines étoiles n'étaient pas toutes fixes par rapport aux autres. On dit même qu'il parvint à en répertorier les éphémérides. Il fut aussi le premier à constater que l'année ne comptait pas 365 jours, mais 365 et un quart. On lui attribue aussi des observations des Hyades et le calcul de la position des Pléiades (calcul d'ailleurs correct depuis le sol égyptien, mais pas depuis la Grèce)[17]. Selon Diogène, Thalès aurait également calculé l'inclinaison du zodiaque, or il est impossible à cette époque de réaliser une telle avancée[54]. Thalès savait aussi tirer profit de ses observations astronomiques. Aristote raconte que Thalès, prévoyant une abondante récolte d'olives, aurait monopolisé les pressoirs pour spéculer sur leurs services ; il voulait ainsi montrer que le sage est capable de faire fortune mais qu'il ne s'en préoccupe pas, préférant la contemplation, la recherche scientifique et la vie honnête[notes 13].
L'éclipse du 28 mai 585
On rapporte qu'il prédit l'éclipse solaire du 585 av. J.-C. qui survint lors d'un combat entre les Mèdes et les Lydiens, la bataille de l'Éclipse[55]. Mais cette prédiction, rapportée par Hérodote (I, 74), relève très certainement de la légende[56]. Elle a été probablement permise par de nombreuses observations empiriques et non par une théorie réelle des éclipses[57]. En effet, à cette époque, la prédiction des éclipses lunaires était relativement connue puisqu'elles se répètent sur un cycle de dix-huit ans (c'est le saros). Une éclipse lunaire est également visible de toute la partie de la Terre orientée vers la Lune. Il en va cependant autrement pour les prédictions des éclipses solaires qui ne sont visibles que pendant quelques minutes sur une portion réduite du globe terrestre. Il semble que Thalès n'avait pas les connaissances requises pour faire de telles prévisions. Cela demande non seulement des moyens géométriques puissants mais aussi des calculs trigonométriques complexes, ainsi que des tables très élaborées, construites à partir d'éphémérides anciennes. Tous ces moyens ne seront mis à la disposition des astronomes que par Hipparque (190 à 120 av. J.-C.) grâce à sa théorie des épicycles. Les Babyloniens possédaient, certes, des éphémérides remontant au moins au VIIIe siècle, mais les autres éléments leur manquaient[58], même s'il est possible d'envisager le fait que Thalès connaissait les observations babyloniennes[59].
Physique

Thalès a également réalisé des constatations physiques ; il est même considéré comme le premier « physicien[5] ».
On lui doit notamment la première connaissance de l'électricité, grâce à deux expériences. Il remarqua d'abord que l'ambre avait la propriété d'attirer les matériaux légers comme le tissu. Le mot « électricité » (ἤλεκτρον, elektron en grec ancien) est par ailleurs donné en référence à l'ambre jaune. Une autre expérience réalisée en Magnésie, vers -600, lui permet de mettre en évidence les propriétés d'aimantation de l'oxyde de fer[60].
Thalès et l'école de Milet
Le fondateur
Thalès passe pour avoir fondé, de retour à Milet, l'école milésienne, qui fait partie de l'école ionienne. Milet était alors la plus puissante cité maritime d'Asie Mineure, dans la région de la Carie, et ce depuis le VIIIe siècle avant notre ère[61]. Selon Jacques Brunschwig (Études sur les philosophies hellénistiques, 1995), l'école de Milet a innové en matière de représentation mentale car elle fait primer la perception visuelle à distance dans l'édification de la connaissance. « Savoir c'est d'abord voir » résume Jacques Brunschwig, qui explique que la perception donne ensuite naissance à la pratique (τέχνη : tekhnè) puis au théorique (ἐπιστήμη : épistémè), processus cognitif que les philosophes de l'école de Milet, dont Thalès, appliquent au questionnement portant sur l'univers[62]. Aétius s'arrête sur cette tendance de Thalès à naturaliser les phénomènes naturels : « Thalès disait que les astres sont faits de terre, mais qu'ils sont embrasés » (Opinions, II, XIII, I).
Thalès est le promoteur d'une « science fondamentalement ouverte, lui permettant de jongler entre ce que nous considérons aujourd’hui comme des disciplines scientifiques diverses et spécialisées ». Selon Karin Mackowiak, il se distingue fondamentalement par sa méthode fondée sur l’acte de « graphein » (γράφειν). C’est en effet « l’écriture qui constitue le point de base primordial, presque individualisée comme discipline en soi, permettant l’érection d’une série de savoirs tous liés les uns aux autres ». Le Milésien utilisait en effet l'écriture sur deux plans : pour le traçage des figures, principal instrument de démonstration en géométrie comme en astronomie, et dans sa maîtrise d’une certaine forme de calcul. « Ces méthodes variées montrent combien la science thalésienne fut conçue non pas comme une fin en soi, censée viser l’accumulation des savoirs, mais comme une pratique instrumentale de l’écriture orientée vers la démonstration de l’existence d’un ordre cosmique et la volonté d’en comprendre le fonctionnement »[63].
Thalès et la pensée milésienne
| L'école ionienne, par Abel Rey[64] | |
|
« Voici le grand tournant… Voici l’entrée en scène de la science, conçue dans son universalité, sous son aspect logique et rationnel. Ce qu’a laissé l’école en résultats positifs : rien. Ce qu’elle a ébauché et légué comme esprit, méthode, pensée : tout ; l’Ionie a fondé une science qui est devenue notre science occidentale, notre civilisation intellectuelle. Elle est la première réalisation du miracle grec et elle en est la clef. » |
Thalès est représentatif de la philosophie de l'école de Milet. Sa théorie de la nature (φύσις : physis), comme ne procédant pas d'une cause exogène (divine par exemple) mais interne, inhérente au vivant, est un trait commun à toutes les figures qui composent cette école. Cette conception, la première de la biologie, est proprement physiologiste[65]. Les membres de l'école ionienne sont ainsi nommés les « physiologues ». Anaximandre et Anaximène sont considérés comme ses successeurs (même si le type de lien qui unit Anaximandre à Thalès varie selon le doxographe : il est son « successeur et élève » pour Simplicios de Cilicie, son « auditeur » pour Hippolyte ou encore son « compagnon » pour Plutarque, note Leopoldo Iribarren[31]). Thalès semble cependant n'avoir rien écrit. On sait cependant que, au sein de cette école, il aurait prononcé les célèbres maximes : « Connais-toi toi-même »[66] et « Ne te porte jamais caution ».
L'école de Milet réalise par ailleurs deux grandes avancées fondatrices : d'une part, elle inaugure la distinction entre le naturel et le surnaturel. De façon plus exacte, ils ne chassent pas le divin de la connaissance du monde, mais la mythologie, en cherchant des causes naturelles aux phénomènes. Ce changement d'attitude fait succéder l'explication naturaliste à l'explication divine classique. D'autre part, les Milésiens mettent en place la discussion des arguments défendus. Admettre la discussion scientifique est une nécessité de l'avancée scientifique et une qualité de la rationalité. Pour cette école, toutes les choses peuvent s'expliquer par la dilatation ou la condensation d'un germe primordial, que ce germe soit l'eau (pour Thalès), le feu (Héraclite d'Éphèse), l'air (Anaximène, Diogène d'Apollonie) ou un principe indéterminé comme l'apeiron (απειρον (Anaximandre). L'idée de matière a ainsi peu à peu été sondée et, de là, les Milésiens lui ont reconnu un principe d'intelligence. Thalès le premier voit dans les mouvements rapides de l'onde une intelligence de la nature[67].
Influence et perception

La pensée milésienne, et en particulier celle de Thalès, a influencé la philosophie de Platon et celle d'Aristote. Pour Bernard Vitrac, comme avec Aristophane, les deux hommes vont faire de Thalès la figure emblématique du philosophe, en lui faisant jouer une fonction au sein de leurs systèmes, d'ailleurs opposés. Dans le Théétète, Thalès est montré comme un philosophe astronome étranger aux affaires de sa cité ; il serait mort en observant le ciel, à la suite d'une chute dans un puits. Au contraire, Aristote s'arrête sur son ingéniosité financière qui lui ont procuré « ses connaissances astronomico-météorologiques en prévoyant une abondante récolte d’olives »[68]. Ce dernier, Aristote, dans sa Métaphysique (A, 3) voit en Thalès « le fondateur (archêgos) d’un type nouveau de philosophie, en rupture avec le thème des généalogies divines »[30]. Pour Jaap Mansfeld, Thalès est le point de départ d'une volonté de donner un sens téléologique à la nature, volonté qui constitue les racines fondatrices de la philosophie péripatéticienne[69]. Thalès a également influencé la politique d'Aristote, qui s'est fondé sur l'école milésienne pour dépasser la pensée politique des IVe et Ve siècles[70].
Notes et références
Notes
- ↑ Hérodote, I, 74, 3-14.
- ↑ Diogène Laërce, Vies, doctrines et sentences des philosophes illustres [détail des éditions] (lire en ligne), « Vie de Thalès », Livre I, 37-38.
- ↑ Diogène Laërce, Vies, doctrines et sentences des philosophes illustres [détail des éditions] (lire en ligne), Livre I, 22.
- ↑ Hérodote, Histoires [détail des éditions] [lire en ligne], I, 75.
- ↑ Hérodote, Histoires [détail des éditions] [lire en ligne], I, 170.
- ↑ Aetius, Opinions, I, III, I.
- ↑ Diogène Laërce, Vie des philosophes illustres, I, 37.
- ↑ Diogène Laërce, Vie des philosophes illustres, Livre I, 39.
- ↑ Platon, Théétète, 174 a.
- ↑ Aristote, Métaphysique, A, III, 983 ; trad. Victor Cousin, 1838.
- ↑ Sénèque, Questions naturelles, III, 14, 1.
- ↑ Archytas de Tarente affirme près de deux siècles plus tard que « seule l'arithmétique, et non la géométrie, peut fournir des démonstrations satisfaisantes », montrant ainsi que la géométrie est encore loin de disposer de l'axiomatisation qu'en donnera Euclide avec ses Éléments.
- ↑ Aristote, Politique, Livre I, XI, 1259 a 6-19.
Références
- ↑ Lucien de Samosate 2015, p. 46, note 7.
- ↑ « Thales of Miletus », sur Encyclopaedia Britannica
- ↑ « THALÈS DE MILET (env. 625-env. 547 av. J.-C.) », sur Universalis.fr
- ↑ André Bonnard, Civilisation grecque : D'Antigone à Sophocle, t. II, Éditions Complexe, , 324 p. (ISBN 9782870274217, lire en ligne), p. 297.
- 1 2 3 4 Kirk, Raven et Schofield 1995, p. 79.
- ↑ Hérodote I, CLXX
- ↑ Kirk, Raven et Schofield 1995, p. 80.
- 1 2 3 Caveing 1997, p. 28.
- ↑ Livre III.
- ↑ Obenga 1995, p. 293-294.
- ↑ Jean-Paul Dumont, Les écoles présocratiques, Paris, Gallimard, , p. 13.
- ↑ Obenga 1995, p. 153.
- ↑ Michel Soutif, Fondements des civilisations de l'Asie : science et culture, Les Ulis, EDP Sciences, coll. « Sciences & histoires », , 372 pages (ISBN 9782759803620), p. 359.
- ↑ Kirk, Raven et Schofield 1995, p. 82.
- ↑ (en) D.R. Dicks, « Thales », Classical Quarterly, vol. 9, nos 3-4, , p. 294-309 (DOI 10.1017/S0009838800041586).
- 1 2 3 Kirk, Raven et Schofield 1995, p. 81.
- 1 2 Kirk, Raven et Schofield 1995, p. 92.
- ↑ John Burnet, L'aurore de la philosophie grecque, Paris, Payot, , p. 46.
- ↑ Jean Voilquin, Les Penseurs grecs avant Socrate. De Thalès de Milet à Prodicos, Paris, Garnier/Flammarion, , p. 46.
- 1 2 Mackowiak 2003, p. 865.
- 1 2 Kirk, Raven et Schofield 1995, p. 98.
- ↑ Obenga 2005, p. 22.
- ↑ Mackowiak 2003, p. 863.
- ↑ Thierry Houlle, 2010, Note 3, p. 101.
- ↑ Kirk, Raven et Schofield 1995, p. 94.
- ↑ Thierry Houlle, 2010, p. 97-98.
- ↑ Thierry Houlle, 2010, p. 99.
- 1 2 Kirk, Raven et Schofield 1995, p. 97.
- 1 2 Obenga 2005, p. 24.
- 1 2 Iribarren 2007, p. 13.
- 1 2 Iribarren 2007, p. 14.
- ↑ Dercyllidas, cité par Théon de Smyrne dans Des connaissances mathématiques utiles pour la lecture de Platon (L.III, XL)
- ↑ Paul Tannery, Pour l'histoire de la science hellène, Felix Alcan, 1887, pp. 70 et suiv.
- ↑ Fritz Hommel, Der babylonische Ursprung der aegyptischen Kultur, Munich, 1892, p. 8.
- ↑ Adolf Hilgenfeld, Judentum und Judenchristentum, p. 98, qui cite : Epiphan. Haeres, 19, 1 et Plutarque, « Sur les Syriens », in Quaest. Conviv., VIII 8, 4 (Mor., 891, 7 sq., Dübner).
- ↑ Theodor Gomperz, Les Penseurs de la Grèce : histoire de la philosophie antique, tome I, livre I, chapitre 1, p. 2.
- ↑ Kirk, Raven et Schofield 1995, p. 99-101
- ↑ Obenga 2005, p. 23.
- ↑ Stella Baruk, « Thalès de Milet », dans Dictionnaire de mathématiques élémentaires [détail des éditions].
- 1 2 3 4 (en) T. Patronis et D. Patsopoulos, « The Theorem of Thales: A Study of the naming of theorems in school Geometry textbooks », The International Journal for the History of Mathematics Education, vol. 1, no 1, , p. 57-68 (lire en ligne)
- ↑ (en) Ilka Agricola et Thomas Friedrich, Elementary Geometry, Providence (R.I.), AMS, , 243 p. (ISBN 978-0-821-84347-5, lire en ligne), p. 50.
- 1 2 Caveing 1997, p. 33-34.
- ↑ Traduction de Charles Zévort XIXe siècle, lire en ligne sur le site remacle.org.
- ↑ Caveing 1997, p. 74-75.
- 1 2 3 4 Caveing 1997, p. 61.
- ↑ Kirk, Raven et Schofield 1995, p. 89.
- 1 2 Caveing 1997, p. 62.
- ↑ Plutarque, Le Banquet des Sept Sages, §2, traduction Victor Bétolaud 1870 lire en ligne sur remacle.org. Il s'agit du pharaon Amasis que Plutarque a cité auparavant.
- ↑ Robert Baccou, Histoire de la science grecque de Thalès à Socrate, Paris, Aubier, , 62-63 p..
- ↑ Mackowiak 2003, p. 867.
- 1 2 Caveing 1997, p. 63.
- ↑ Jean-Marie Nicolle, Histoire des méthodes scientifiques : du théorème de Thalès au clonage, Rosny, Editions Bréal, , 156 p. (ISBN 9782749506494), p. 17-18.
- ↑ Denis Guedj, Le Théorème du Perroquet, Seuil, chap. 3.
- 1 2 Kirk, Raven et Schofield 1995, p. 87-88.
- ↑ (en) Thomas Worthen, « Herodotos's report on thales' eclipse », Electronic Antiquity, vol. 3, no 7, (ISSN 1320-3606, lire en ligne).
- ↑ Observatoire de Paris, Le manuel des éclipses, Paris, Institut de mécanique céleste et de calcul des éphémérides, , p. 12.
- ↑ Kirk, Raven et Schofield 1995, p. 85.
- ↑ Árpád Szabó (trad. Michel Federspiel), L'aube des mathématiques grecques, Paris, Vrin, coll. « Mathésis », , 384 p. (ISBN 9782711612796, lire en ligne), p. 25.
- ↑ Charles H. Kahn, Anaximander and the Origins of Greek Cosmology, 1960, Hackett, in Kirk, Raven et Schofield 1995, p. 86.
- ↑ Fred Gardiol, Électromagnétisme, vol. 3, PPUR, coll. « Traité d'électricité », , 468 p. (ISBN 978-2-880-74508-0, lire en ligne), p. 3.
- ↑ Obenga 2005, p. 21.
- ↑ Claude Meyer, Une histoire des représentations mentales : contribution à une archéologie de la société de la connaissance, Paris, L'Harmattan, coll. « Pour comprendre », , 343 pages (ISBN 9782296035379, lire en ligne), p. 23-25.
- ↑ Mackowiak 2003, p. 862.
- ↑ Abel Rey, La jeunesse de la science grecque, La Renaissance du livre, , p. 19-20.
- ↑ Hendrik (Henk) Cornelis Dirk de Wit, Histoire du développement de la biologie, vol. 1, Lausanne, PPUR presses polytechniques, coll. « Biologie », , 404 p. (ISBN 978-2-880-74233-1, lire en ligne), p. 14.
- ↑ Diogène Laërce, Vies, doctrines et sentences des philosophes illustres [détail des éditions] (lire en ligne) (ch. I, §40).
- ↑ Alfred Fouillé, La philosophie de Platon : Esthétique, morale et religion platoniciennes, vol. 2, Paris/Paris, L'Harmattan, coll. « La philosophie de Platon », , 377 p. (ISBN 978-2-357-48028-5, lire en ligne), p. 256-258.
- ↑ Vitrac 2010, p. 6.
- ↑ (en) Jaap Mansfeld, « Aristotle and others on Thales, or the beginnings of natural philosophy », Mnemosyne, no 38, , p. 109-129 (présentation en ligne).
- ↑ Sylvie Vilatte, Espace et temps : La cité aristotélicienne de la Politique, vol. 141, Presses Universitaires de Franche-Comté, coll. « Centre de recherches d'histoire ancienne », , 432 p. (ISBN 978-2-251-60552-4, lire en ligne), p. 259-264.
Annexes
Bibliographie
- Luc Brisson (dir.) et Michel Narcy (trad. du grec ancien par Michel Narcy), Théétète : Platon, Œuvres complètes, Paris, Flammarion, (1re éd. 2006), 2204 p. (ISBN 978-2081218109).
- Luc Brisson (dir.) et Frédérique Ildefonse (trad. du grec ancien), Protagoras : Platon, Œuvres complètes, Paris, Flammarion, (1re éd. 2006), 2204 p. (ISBN 978-2081218109).
- Émile Chambry, Émeline Marquis, Alain Billault et Dominique Goust (trad. du grec ancien par Émile Chambry), Lucien de Samosate : Œuvres complètes, Paris, Éditions Robert Laffont, coll. « Bouquins », , 1248 p. (ISBN 9782221109021).
Sources historiographiques
- Hérodote, Histoires [détail des éditions] [lire en ligne] (I, 74-75 et 170 ; II, 20 et 109)
- Platon, Théétète (174 a) et Protagoras (343 a)
- Aristote, Politique (I, XI, 1259 a 6 [8] - [13]), Métaphysique (A, III, 983 b 6), Du ciel (II, XIII, 294 a, 28), De l'âme (I, V, 411 a 7 et I, II, 405 a 19) et Scolie à Platon, La République (X, 600 a)
- Callimaque de Cyrène, Iambes (fr. 94)
- (en) Clément d'Alexandrie, Stromates (lire en ligne) (I, 65)
- Tatien le Syrien, Discours aux Grecs (41)
- Eusèbe de Césarée, Chronographie, Contre Julien
- Cicéron, De divinatione [détail des éditions] [lire en ligne] (I, 49, 111, 112), De natura deorum [détail des éditions] [lire en ligne] (I, X, 25)
- Sénèque, Questions naturelles (lire en ligne) (III, 13 et 14, IV, 2, 22 ; VI, 6, 1)
- Plutarque de Chéronée, Vies parallèles [détail des éditions] [lire en ligne], Solon (2 ; 12), Isis et Osiris (34), Le Banquet des Sept Sages (2), Pourquoi la prophétesse Pythie ne rend plus les oracles en vers ? (18, 402, E)
- Hippolyte de Rome, Réfutation de toutes les hérésies (I, 1)
- Diogène Laërce, Vies, doctrines et sentences des philosophes illustres [détail des éditions] (lire en ligne) (I, 22-40)
- Pline l'Ancien, Histoire naturelle [détail des éditions] [lire en ligne] (II, 53, XVIII, 213, XXXVI, 82)
- Proclus, Commentaire sur le premier livre d'Euclide (65, 3)
- Flavius Josèphe, Contre Apion (I, 2)
- Aetius, Opinions (I, III, I)
- (en + grc) Souda (lire en ligne)
- Jamblique, Vie pythagorique (12)
- Simplicios de Cilicie, Commentaire sur la Physique d'Aristote (23, 21 et 458, 23)
- Apulée, Florides (18)
- Julien, Discours (III, 162, 2)
- Galien, Sur les humeurs d'Hippocrate (I, I)
- Ausone, Le Jeu des Sept Sages
Fragments et témoignages
Études
Monographies
- Maurice Caveing, « La percée des Ioniens », dans Maurice Caveing, La figure et le nombre: recherches sur les premières mathématiques des Grecs, vol. 2, Presses Universitaires du Septentrion, coll. « Histoire des sciences », , 424 p. (ISBN 978-2-859-39494-3, lire en ligne)
- (en) Theodor Gomperz (trad. Auguste Reymond), Les Penseurs de la Grèce : histoire de la philosophie antique, t. 1, Payot, , « 1, II »
- Thierry Houlle, L'eau et la pensée grecque : Du mythe à la philosophie, Paris, L'Harmattan, coll. « L'ouverture philosophique », , 216 p. (ISBN 978-2-296-11219-3, lire en ligne), chap. 2 (« L'eau-origine »)
- Geoffrey Stephen Kirk, John Earle Raven et Malcolm Schofield, Les philosophes présocratiques : Une histoire critique avec un choix de textes, vol. 16, Fribourg, Saint-Paul, coll. « Vestigia », , 562 p. (ISBN 978-2-204-05263-4, lire en ligne)
- Robert Lahaye, La Philosophie ionienne. L'École de Milet, Paris, Édition du Cèdre,
- Geoffrey Lloyd, Les débuts de la science grecque : De Thalès à Aristote, La Découverte, , 189 p. (ISBN 978-2-707-11943-8)
- Théophile Obenga, La géométrie égyptienne : contribution de l'Afrique antique à la mathématique mondiale, vol. 1, L'Harmattan, coll. « Travaux de l'Institut d'Egyptologie Cheikh Anta Diop », , 338 p. (ISBN 978-2-738-42977-3, lire en ligne), « Appendice II : Thalès et la science égyptienne : témoignages anciens »
- Théophile Obenga, L'Égypte, la Grèce et l'école d'Alexandrie : Histoire interculturelle dans l'antiquité, aux sources égyptiennes de la philosophie grecque, L'Harmattan, , 261 p. (ISBN 978-2-747-59199-7, lire en ligne)
Articles
- Leopoldo Iribarren, « Du muthos au logos : Le détour par la pragmatique des discours », Labyrinthe, no 28, (lire en ligne)
- Karin Mackowiak, « Les savoirs de Thalès et de Kadmos : Histoire et représentations religieuses en Grèce ancienne », Annales. Histoire, Sciences Sociales, no 4, , p. 859-876 (DOI 10.1017/S0395264900005096, lire en ligne)
- Paul Tannery, « Thalès et ses emprunts à l'Égypte », Revue philosophique de la France et de l'étranger, vol. IX, , p. 299 à 318
- Bernard Vitrac, « Figures du mathématicien et représentations des mathématiques en Grèce ancienne (VIe-IVe s. avant notre ère) », dans Actes du Colloque International « Le savoir public » organisé par A. Macé à l’Université de Franche-Comté de Besançon, les 8-10 octobre 2008, Centre Louis Gernet de recherches comparées sur les sociétés anciennes, CNRS, EHESS, (lire en ligne)
- Pierre-Jean Dessertine, « La leçon de Thalès sur le sens des premières cosmologies », Comité de liaison enseignants et astronomes#Les Cahiers Clairaut, no 82, (lire en ligne)
- (en) « Thales of Miletus (c. 620 BCE – c. 546 BCE) », dans Internet Encyclopedia of Philosophy (lire en ligne)
Articles connexes
- Cosmologie
- Figure de la Terre dans l'Antiquité
- Sciences grecques
- Théorème de Thalès
Liens externes
- Ressources relatives aux beaux-arts :
- (en) British Museum
- (de + en + la) Sandrart.net
- Ressource relative à l'astronomie :
- Ressource relative à la santé :
- Ressource relative à la recherche :
- Notices dans des dictionnaires ou encyclopédies généralistes :

![N1 [pt] pt](https://img.franco.wiki/i/hiero_N1.png.webp)
![N35 [n] n](https://img.franco.wiki/i/hiero_N35.png.webp)