Loi log-normale

Loi Log-normale
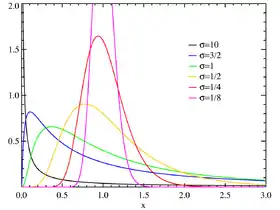Densité de probabilité μ=0


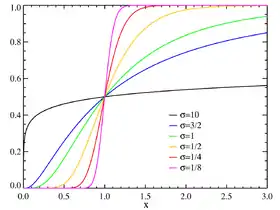Fonction de répartition μ=0

Paramètres	$\sigma >0$ $-\infty <\mu <\infty$
Support	$]0;+\infty [\!$
Densité de probabilité	${\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {\left[\ln(x)-\mu \right]^{2}}{2\sigma ^{2}}}\right)$
Fonction de répartition	${\frac {1}{2}}+{\frac {1}{2}}\mathrm {erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]$
Espérance	$\mathrm {e} ^{\mu +\sigma ^{2}/2}$
Médiane	$\mathrm {e} ^{\mu }$
Mode	$\mathrm {e} ^{\mu -\sigma ^{2}}$
Variance	$(\mathrm {e} ^{\sigma ^{2}}\!\!-1)\mathrm {e} ^{2\mu +\sigma ^{2}}$
Asymétrie	$(\mathrm {e} ^{\sigma ^{2}}\!\!+2){\sqrt {\mathrm {e} ^{\sigma ^{2}}\!\!-1}}$
Kurtosis normalisé	$\mathrm {e} ^{4\sigma ^{2}}\!\!+2\mathrm {e} ^{3\sigma ^{2}}\!\!+3\mathrm {e} ^{2\sigma ^{2}}\!\!-6$
Entropie	${\frac {1}{2}}+{\frac {1}{2}}\ln(2\pi \sigma ^{2})+\mu$

En théorie des probabilités et statistique, une variable aléatoire X est dite suivre une loi log-normale de paramètres $\mu$ et $\sigma ^{2}$ si la variable $Y=\ln(X)$ suit une loi normale d'espérance $\mu$ et de variance $\sigma ^{2}$ .

Cette loi est parfois appelée loi de Galton. Elle est habituellement notée $\operatorname {Log-{\mathcal {N}}} (\mu ,\,\sigma ^{2})$ dans le cas d'une seule variable ou $\operatorname {Log-{\mathcal {N}}} (\mu ,\,\Sigma )$ dans un contexte multidimensionnel.

Une variable peut être modélisée par une loi log-normale si elle est le résultat de la multiplication d'un grand nombre de petits facteurs indépendants^[1].

Caractérisation

Densité

La loi log-normale de paramètres $\mu$ et $\sigma$ admet pour densité de probabilité

f_{X}(x;\mu ,\sigma )={\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}\right)={\frac {1}{x}}f_{Y}(\ln(x);\mu ,\sigma )

pour $x>0$ . Les paramètres $\mu$ et $\sigma$ sont l'espérance et l'écart type du logarithme de la variable (puisque par définition, le logarithme de la variable est distribué selon une loi normale d'espérance $\mu$ et d'écart-type $\sigma$ ).

Fonction de répartition

Par intégration de la fonction de densité, il vient que la fonction de répartition s'exprime en fonction de la fonction d'erreur $erf$ :

F_{X}(x;\mu ,\sigma )={\frac {1}{2}}+{\frac {1}{2}}\mathrm {erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]=F_{Y}(\ln(x);\mu ,\sigma ).

Moments

Tous les moments existent et sont donnés par :

\mu _{k}=\mathrm {e} ^{k\mu +k^{2}\sigma ^{2}/2}.

Espérance et écart-type

L'espérance est

\mathrm {E} (X)=\mathrm {e} ^{\mu +\sigma ^{2}/2}

et la variance est

\mathrm {Var} (X)=(\mathrm {e} ^{\sigma ^{2}}-1)\mathrm {e} ^{2\mu +\sigma ^{2}}.\,

Des relations équivalentes permettent d'obtenir $\mu$ et $\sigma$ étant données l'espérance et l'écart-type :

\left\{{\begin{aligned}\mu &=\ln(\mathrm {E} (X))-{\frac {1}{2}}\sigma ^{2}\\\sigma ^{2}&=\ln \left(1+{\frac {\mathrm {Var} (X)}{(\mathrm {E} (X))^{2}}}\right)\end{aligned}}\right.

Autres relations

\mathrm {Cov} (X,Y)=\mathrm {E} (X)\,\sigma ^{2}(Y)

\mathrm {Cov} (X,Z)=\mathrm {E} (X)\,\mathrm {Cov} (Y,Z)

\mathrm {Cor} (X,Z)=\mathrm {Cor} (Y,Z)\,\sigma (Y)\,(\mathrm {e} ^{\sigma ^{2}(Y)}-1)^{-1/2}

où $Z$ est une variable normale quelconque de variance $\sigma ^{2}(Z)$ .

Pour deux variables log-normales, les relations sont indiquées dans le contexte multidimensionnel ci-dessous.

Comportement de la densité

Il suffit de dériver la densité de la loi log-normale pour vérifier les résultats suivants :

En x = 0, la singularité de la densité n’est qu’apparente car elle satisfait

\lim _{x\to 0+}f_{X}(x;\mu ,\sigma )=0.

La fonction peut ainsi être prolongée en 0 de manière continue en lui attribuant la valeur 0.

Lorsque la valeur du mode est très faible (

\mu =0\,

\sigma =10\,

comme dans le cartouche ci-dessus), le graphe de la densité semble diverger en 0, ce qui n’est formellement pas le cas.

Comme l’indique son mode, la densité admet un maximum en $x_{m}=\exp(\mu -\sigma ^{2})$ où sa valeur atteint

f_{X}(x_{m};\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\,\exp \left({\frac {\sigma ^{2}}{2}}-\mu \right).

Loi log-normale multidimensionnelle

Un vecteur aléatoire ${\boldsymbol {X}}$ est dit suivre une loi log-normale multidimensionnelle de paramètres ${\boldsymbol {\mu }}\in \mathbb {R} ^{N}$ et ${\boldsymbol {\Sigma }}\in {\mathcal {M}}_{N}(\mathbb {R} )$ si le vecteur ${\boldsymbol {Y}}=\ln({\boldsymbol {X}})$ (composante par composante) suit une loi normale multidimensionnelle dont le vecteur des espérances est ${\boldsymbol {\mu }}$ et la matrice de covariance est ${\boldsymbol {\Sigma }}$ .

Cette loi est habituellement notée $\operatorname {Log-{\mathcal {N}}} ({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }})$ .

La densité de probabilité et la fonction de répartition sont les suivantes :

f_{{\boldsymbol {X}},{\boldsymbol {\mu }},{\boldsymbol {\Sigma }}}\left({\boldsymbol {x}}\right)={\frac {1}{\prod _{i=1}^{N}x_{i}}}\;f_{{\boldsymbol {Y}},{\boldsymbol {\mu }},{\boldsymbol {\Sigma }}}\left(\ln({\boldsymbol {x}})\right)

où

f_{{\boldsymbol {Y}},{\boldsymbol {\mu }},{\boldsymbol {\Sigma }}}()

est la densité de

{\boldsymbol {Y}}

F_{{\boldsymbol {X}},{\boldsymbol {\mu }},{\boldsymbol {\Sigma }}}\left({\boldsymbol {x}}\right)=F_{{\boldsymbol {Y}},{\boldsymbol {\mu }},{\boldsymbol {\Sigma }}}\left(\ln({\boldsymbol {x}})\right)

où

F_{{\boldsymbol {Y}},{\boldsymbol {\mu }},{\boldsymbol {\Sigma }}}()

est la fonction de répartition de

{\boldsymbol {Y}}

Les espérances et covariances sont données par les relations (valables également dans le cas dégénéré) :

\operatorname {E} \left([{\boldsymbol {X}}]_{i}\right)=\mathrm {e} ^{{\boldsymbol {\mu }}_{i}+{\frac {1}{2}}{\boldsymbol {\Sigma }}_{ii}},

\operatorname {Cov} \left([{\boldsymbol {X}}]_{i},[{\boldsymbol {X}}]_{j}\right)=\operatorname {E} \left([{\boldsymbol {X}}]_{i}\right)\operatorname {E} \left([{\boldsymbol {X}}]_{j}\right)\;(\mathrm {e} ^{{\boldsymbol {\Sigma }}_{ij}}-1).

Eléments de justification

Une évaluation de la densité de ${\boldsymbol {X}}$ peut se baser sur la définition informelle de la densité, en exploitant celle de ${\boldsymbol {Y}}$ (loi normale multidimensionnelle) après avoir effectué le changement de variable

[{\boldsymbol {X}}]_{i}=\exp {\left([{\boldsymbol {Y}}]_{i}\right)}.

Les expressions relatives à l’espérance et à la covariance se déduisent de la fonction génératrice des moments de la loi normale multidimensionnelle, soit

M_{\boldsymbol {Y}}({\boldsymbol {t}})=\exp \left({\boldsymbol {\mu }}^{\top }{\boldsymbol {t}}+{\frac {1}{2}}{\boldsymbol {t}}^{\top }{\boldsymbol {\Sigma }}{\boldsymbol {t}}\right).

A l’aide du même changement de variable, on obtient respectivement

avec $t_{k}=\delta _{ik}$ (symbole de Kronecker) : $\operatorname {E} \left([{\boldsymbol {X}}]_{i}\right)=\exp \left({\boldsymbol {\mu }}_{i}+{\frac {1}{2}}{\boldsymbol {\Sigma }}_{ii}\right)$
avec $t_{k}=\delta _{ik}+\delta _{jk}$ : $\operatorname {E} \left([{\boldsymbol {X}}]_{i}\,[{\boldsymbol {X}}]_{j}\right)=\exp \left({\boldsymbol {\mu }}_{i}+{\boldsymbol {\mu }}_{j}+{\frac {1}{2}}{\boldsymbol {\Sigma }}_{ii}+{\frac {1}{2}}{\boldsymbol {\Sigma }}_{jj}+{\boldsymbol {\Sigma }}_{ij}\right).$ La conclusion découle de $\operatorname {Cov} \left([{\boldsymbol {X}}]_{i},[{\boldsymbol {X}}]_{j}\right)=\operatorname {E} \left([{\boldsymbol {X}}]_{i}\,[{\boldsymbol {X}}]_{j}\right)-\operatorname {E} \left([{\boldsymbol {X}}]_{i}\right)\operatorname {E} \left([{\boldsymbol {X}}]_{j}\right).$

Remarques :

Attention : la matrice de terme générique $\mathrm {e} ^{{\boldsymbol {\Sigma }}_{ij}}$ n’a rien à voir avec l’exponentielle de la matrice ${\boldsymbol {\Sigma }}.$
${\boldsymbol {\Sigma }}$ peut être singulière (cas dégénéré) sans nécessairement impliquer que $C$ le soit. Exemple : ${\boldsymbol {\Sigma }}={\begin{pmatrix}1&-0,5&0,5\\-0,5&1&0,5\\0,5&0,5&1\\\end{pmatrix}}.$
À toute matrice semi-définie positive, on peut associer un vecteur normal dont elle est la covariance. Par contre, il n’existe pas nécessairement un vecteur log-normal dont elle soit la covariance. En effet, avec la relation $C_{ij}=\mathrm {e} ^{{\boldsymbol {\Sigma }}_{ij}}-1$ , toute matrice ${\boldsymbol {\Sigma }}$ semi-définie positive conduit à une matrice $C$ semi-définie positive, mais l’inverse n’est généralement pas vrai. Un contre-exemple où $C$ est définie positive alors que ${\boldsymbol {\Sigma }}$ ne l’est pas : $C={\begin{pmatrix}1&-0,5&0,9\\-0,5&1&-0,5\\0,9&-0,5&1\\\end{pmatrix}}.$

Positivité de la covariance

Les relations caractérisant les espérances et les covariances pouvant se déduire de la fonction génératrice des moments de la loi normale multidimensionnelle, la matrice de covariance doit naturellement être semi-définie positive. Ce résultat est ici présenté de manière directe.

Puisque les espérances $\operatorname {E} \left([{\boldsymbol {X}}]_{i}\right)$ sont strictement positives, $\operatorname {Cov} \left([{\boldsymbol {X}}]_{i},[{\boldsymbol {X}}]_{j}\right)$ est semi-définie positive si et seulement si $\mathrm {e} ^{{\boldsymbol {\Sigma }}_{ij}}-1$ l’est : il suffit alors de considérer uniquement cette dernière matrice. Puisque la positivité de ${\boldsymbol {\Sigma }}$ est la seule propriété qui est exploitée, on notera cette matrice $A$ qui ne fait plus référence à une covariance.

Lemme — Soit $A$ une matrice semi-définie positive et $p$ un entier positif. Alors la matrice $A^{(p)}$ définie par $(A^{(p)})_{ij}=(A_{ij})^{p}$ l’est également.

Proposition 1 — Si $A$ est semi-définie positive, alors $C_{ij}=\mathrm {e} ^{A_{ij}}-1\,$ l’est également.

Résultats relatifs au spectre de $C$ indiquant des bornes pour ses valeurs propres :

Proposition 2 — Soit $A$ semi-définie positive et notons

$0\leq d_{-}\leq d_{+}$ les valeurs extrêmes des coefficients diagonaux $A_{ii}$ ,
$0\leq \lambda _{-}\leq \lambda _{+}$ les valeurs propres extrêmes de $A$ ,
$0\leq \lambda _{-}^{(p)}\leq \lambda _{+}^{(p)}$ les valeurs propres extrêmes de $A^{(p)}$ ,
$0\leq \mu _{-}\leq \mu _{+}$ les valeurs propres extrêmes de $C_{ij}=\mathrm {e} ^{A_{ij}}-1.$

Alors

$\lambda _{-}^{(p)}\,d_{-}\leq \lambda _{-}^{(p+1)}\leq \lambda _{+}^{(p+1)}\leq \lambda _{+}^{(p)}\,d_{+},$
$\lambda _{-}\,\mathrm {e} ^{d_{-}}\leq \mu _{-}\leq \mu _{+}\leq \lambda _{+}\,\mathrm {e} ^{d_{+}}.$

Preuves

Preuve du Lemme :

Puisque $A$ est diagonalisable, elle peut s’écrire sous la forme $A=ODO^{T}$ où $O$ est une matrice orthogonale (dont les colonnes sont les vecteurs propres de $A$ ) et où $D$ est une matrice diagonale dont les coefficients sont précisément les valeurs propres de $A$ .

Supposons par induction sur $p$ que $A^{(p)}$ soit positive. Pour tout vecteur $x$ , on peut ainsi écrire

x^{T}A^{(p+1)}x=\sum _{ij}(A_{ij})^{p+1}x_{i}x_{j}=\sum _{ij}(A_{ij})^{p}A_{ij}\,x_{i}x_{j}=\sum _{ijk}(A_{ij})^{p}\,(O_{ik}D_{k}O_{jk})\,x_{i}x_{j}=

=\sum _{k}D_{k}\sum _{ij}(A_{ij})^{p}\,(O_{ik}x_{i})\,(O_{jk}x_{j})=\sum _{k}\,D_{k}\,(y^{(k)})^{T}\,A^{(p)}\,y^{(k)}\geq 0

où $y^{(k)}$ est un vecteur défini par $y_{i}^{(k)}=O_{ik}\,x_{i}.$

L’inégalité découle de la positivité de $A$ (impliquant $D_{k}\geq 0$ ) et de celle de $A^{(p)}$ par hypothèse d’induction.

Cette inégalité montre que la positivité se préserve de proche en proche.

Preuve de la Proposition 1 :

Il suffit de remarquer que $C$ est une somme de matrices semi-définies positives par la relation

C=\sum _{p\geq 1}{\frac {1}{p!}}A^{(p)}.

Preuve de la Proposition 2 :

En repartant de l’égalité du Lemme où $x$ est un vecteur propre de $A^{(p)}$ de norme 1 pour la plus petite valeur propre $\lambda _{-}^{(p+1)}$ , on en tire

\lambda _{-}^{(p+1)}=\sum _{k}\,D_{k}\,(y^{(k)})^{T}\,A^{(p)}\,y^{(k)}\geq \lambda _{-}^{(p)}\sum _{k}\,D_{k}\,\left\|y^{(k)}\right\|^{2}=\lambda _{-}^{(p)}\sum _{i}\,A_{ii}\,(x_{i})^{2}\geq \lambda _{-}^{(p)}\,d_{-}.

Le même procédé s’appliquant pour $\lambda _{+}^{(p+1)}$ , on en déduit le point 1.

Finalement, il suffit de reprendre le développement de $C$ indiqué dans la preuve de la proposition 1 pour montrer le point 2.

Remarque : au vu des minorations (majorations) brutales (en particulier celles de la seconde inégalité), les bornes obtenues ne sont pas optimales.

Loi de Gibrat

Historiquement nommée loi de l'effet proportionnel, puis parfois loi log-normale à 3 paramètres, cette loi est une généralisation de la loi log-normale obtenue par l’ajout d’une simple translation en posant

Y=\ln(X-X_{0})

Elle est notée $\operatorname {Log-{\mathcal {N}}} (X_{0},\,\mu ,\,\sigma ^{2})$ et ne concerne que des valeurs $X>X_{0}.$ Son utilisation devrait se limiter aux situations où cette borne inférieure possède un sens physique et dont la valeur est connue.

Domaines d'application

Marchés financiers

La loi log-normale est souvent utilisée en analyse quantitative pour représenter les cours des instruments financiers (notamment les actions, cours de change, taux d'intérêt). Avec la loi multidimensionnelle, il est possible d’envisager des modèles susceptibles de considérer différents titres et leurs corrélations, ce qui permet ainsi d’appréhender et de quantifier les risques d'un portefeuille.

Les cours n’étant pas négatifs, il est pertinent d'exprimer leurs variations sous forme relative (en pourcentage) et, en première approximation, les cours sont décrits par une loi log-normale.

D’autre part, une raison plus profonde réside dans l’estimation de la volatilité du cours d’une action qui peut être définie par l’écart-type du rendement :

Si le prix d’une cotation passe de P1 à P2 durant une période d’un jour, le rendement journalier est r = P2 / P1 -1 et, à ce rythme, l’expression continue du rendement R annuel satisfait (T = 365 jours) :

\mathrm {e} ^{R}=(1+r)^{T}=(P_{2}/P_{1})^{T},\;ie\;R=T\,[\ln(P_{2})-\ln(P_{1})].

On voit alors apparaître le lien entre la volatilité $\sigma (R)$ et la variable aléatoire qui affecte le logarithme du cours.

Autres domaines

Le nombre de mots dans une phrase peut être modélisé par une loi log-normale^[2].
La répartition des revenus dans la population peut également être approchée par une loi log-normale.
En biologie, on peut l'utiliser pour modéliser le poids des organismes vivants.
En hydrologie, les débits mensuels de petits bassins versants à régimes pluviaux.
En génomique, il a été observé que les taux de mutations varient le long des chromosomes et leur distribution peut être approximée par une loi log-normale.
En mécanique des fluides, la loi log-normale donne une bonne approximation de la fonction de distribution en taille de gouttes à la sortie d'un aérosol ou d'un jet pulvérisé.

Notes et références

↑ Bernard Delmas, Statistique descriptive, Paris, Nathan, 1996, p. 143.
↑ Stéphane Tufféry, Data mining et statistique décisionnelle : l'intelligence des données, p. 347 sur Google Livres.