En théorie des probabilités, une variable aléatoire à densité est une variable aléatoire réelle, scalaire ou vectorielle, pour laquelle la probabilité d'appartenance à un domaine se calcule à l'aide d'une intégrale sur ce domaine.

Calcul de la probabilité d’un intervalle [a,b]
pour une variable X de densité f.
La fonction à intégrer est alors appelée « fonction de densité » ou « densité de probabilité », égale[1] (dans le cas réel) à la dérivée de la fonction de répartition.
Les densités de probabilité sont les fonctions essentiellement positives et intégrables d'intégrale 1 sur  .
.
Informellement, une densité de probabilité peut être vue comme la limite d'un histogramme : si on dispose d'un échantillon suffisamment important de valeurs d'une variable aléatoire à densité, représenté par un histogramme des fréquences relatives des différentes classes de valeurs, alors cet histogramme va ressembler à la densité de probabilité de la variable aléatoire, pourvu que les classes de valeurs soient suffisamment étroites.
Variable aléatoire réelle
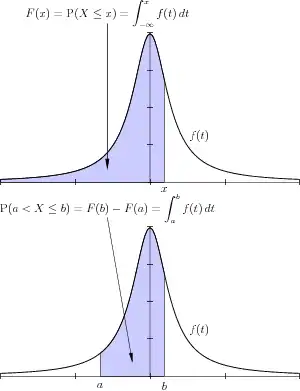
Lien entre la densité, f et la fonction de répartition (haut), et, plus généralement, les probabilités (bas).
Une variable aléatoire réelle X est dite à densité s'il existe une fonction f positive et intégrable sur  ,
appelée fonction de densité, telle que pour tout
,
appelée fonction de densité, telle que pour tout  on ait
on ait  .
.
Dans ce cas, pour tout réel a on trouve  . En outre, la fonction de répartition
. En outre, la fonction de répartition  est continue et même presque partout dérivable, et sa dérivée est alors presque partout égale à la fonction de densité.
est continue et même presque partout dérivable, et sa dérivée est alors presque partout égale à la fonction de densité.
On obtient aussi  , ce qui correspond à la somme des probabilités élémentaires pour une variable aléatoire discrète, mais la fonction de densité peut très bien avoir des valeurs strictement supérieures à 1.
, ce qui correspond à la somme des probabilités élémentaires pour une variable aléatoire discrète, mais la fonction de densité peut très bien avoir des valeurs strictement supérieures à 1.
Le support d'une variable aléatoire à densité est l'adhérence de l'ensemble des réels pour lesquels la fonction de densité est essentiellement non nulle, c'est-à-dire le complémentaire de la réunion des intervalles ouverts sur lesquels la fonction de répartition est constante.
En traçant la représentation graphique de la densité de probabilité, la probabilité  se lit comme l'aire sous la courbe sur l'intervalle [a , b].
se lit comme l'aire sous la courbe sur l'intervalle [a , b].
Exemples
On peut classer les lois à densité selon leur type de support : borné, semi-infini ou infini. Chacune d'elles représente en général une famille de lois dépendant d'un ou plusieurs paramètres.
Parmi les lois à densité à support borné, on trouve notamment les lois uniforme, triangulaire, ou la loi bêta.
Beaucoup de lois à densité ont pour support l'ensemble  , comme la loi exponentielle, le χ² (« khi-deux »), la loi Gamma ou la loi de Pareto.
, comme la loi exponentielle, le χ² (« khi-deux »), la loi Gamma ou la loi de Pareto.
D'autres ont pour support l'ensemble  comme la loi normale et la loi de Cauchy.
comme la loi normale et la loi de Cauchy.
Critères d'existence d'une densité
En vertu d'un théorème dû à Lebesgue[2], la fonction de répartition d'une variable aléatoire réelle X étant croissante, elle est dérivable presque partout sur  , et la dérivée ainsi obtenue est positive et intégrable sur
, et la dérivée ainsi obtenue est positive et intégrable sur  , d'intégrale inférieure ou égale à 1.
, d'intégrale inférieure ou égale à 1.
Une variable aléatoire réelle est à densité si et seulement si l'un des critères équivalents suivants est satisfait :
- Sa fonction de répartition est absolument continue ;
- L'intégrale sur
 de la dérivée de sa fonction de répartition vaut 1.
de la dérivée de sa fonction de répartition vaut 1.
La continuité de la fonction de répartition exclut les variables aléatoires discrètes mais ne suffit pas pour définir une fonction de densité, comme dans le cas d'une variable aléatoire dont la fonction de répartition est l'escalier de Cantor. Une telle loi est dite diffuse, mais la dérivée de la fonction de répartition est presque partout nulle.
On dispose également d'une condition suffisante souvent utilisée dans les cas pratiques : une variable aléatoire réelle dont la fonction de répartition est continue et de classe  par morceaux sur
par morceaux sur  est une variable à densité.
est une variable à densité.
Espérance, variance et moments
Soit X une variable aléatoire réelle ayant une densité de probabilité f. D'après le théorème de transfert, X possède un moment d'ordre k si et seulement si l'intégrale

est finie. On a dans ce cas

En particulier, lorsque le moment d'ordre 2 existe :

et, d'après le théorème de König-Huyghens,

La définition qui suit est une reformulation de la définition intégrale proposée en début d'article. C'est la définition utilisée en général par les physiciens, en particulier ceux issus du domaine de la physique statistique.
Si dt est un nombre réel positif infiniment petit, alors la probabilité que X soit inclus dans l'intervalle [t , t + dt] est égale à f (t) dt soit :

Cette « définition » est très utile pour comprendre intuitivement à quoi correspond une densité de probabilité, et elle est correcte dans beaucoup de cas importants. On peut tracer une analogie avec la notion de densité de masse, ou encore avec la notion de densité de population. Une formulation plus mathématique serait

ce qui permet de comprendre en quoi la définition donnée en physique n'est pas complètement rigoureuse :

et il est alors facile de vérifier que si f possède une limite à droite en t, qu'on note f(t+), on a alors :

ce qui corrobore la définition physique lorsque f est continue à droite en t, mais la met en défaut quand f(t) ≠ f(t+). Bien sûr, les densités de probabilités usuelles sont continues à droite sauf éventuellement en un nombre fini (et en un petit nombre) de points.
Ce genre d'interprétation infinitésimale (ou issue de la physique) s'étend aux dimensions d ≥ 2 (voir la section suivante).
Densité de la médiane de 9 variables i.i.d. :
Soit  une suite de 9 v.a.r. i.i.d. de même densité f et de même fonction de répartition F. Notons M la médiane de cette suite. Alors :
une suite de 9 v.a.r. i.i.d. de même densité f et de même fonction de répartition F. Notons M la médiane de cette suite. Alors :

On peut voir cela comme une suite de 9 expériences aléatoires indépendantes faites dans les mêmes conditions, avec à chaque fois trois issues : « Xi ≤ t », « t < Xi < t + dt » et « t + dt ≤ Xi », de probabilités respectives F(t), f(t) dt et 1 – F(t + dt), donc la probabilité ci-dessus est donnée par la loi multinomiale de paramètres 3, 9 et (F(t) , f(t) dt , 1 – F(t + dt)). Ainsi :

et la densité de M est

Cette méthode est détaillée dans le livre de David[3]. Un résultat plus général se trouve dans Statistique d'ordre.
Densité de la médiane de 9 variables i.i.d. (bis) :
Pour le calcul de la densité de la médiane de 9 variables i.i.d., une solution plus rigoureuse que celle de la section précédente, mais plus lourde, est de calculer la fonction de répartition de la médiane, puis de la dériver. On reconnait un schéma de Bernoulli : le nombre d'indices i tels que {Xi ≤ t } suit une loi binomiale de paramètres 9 et F(t).
![{\displaystyle {\begin{array}{rl}\mathbb {P} \left(M\leq t\right)&=F_{M}(t)=\mathbb {P} \left({\text{au moins 5 des 9 }}X_{i}{\text{ sont }}\leq t\right)\\[5pt]&={\displaystyle \sum _{j=5}^{9}{9 \choose j}F(t)^{j}(1-F(t))^{9-j}.}\end{array}}}](https://img.franco.wiki/i/23d866de48c73c8f7a0f939561acffa0d0ed54e5.svg)
En dérivant, on trouve :

Après quelques manipulations sur les coefficients binomiaux, tous les termes de cette somme se télescopent, sauf une partie du premier terme, ce qui donne :

puis

Pour les deux dernières égalités, se référer aux pages sur la fonction bêta et sur la fonction gamma. Il en découle que fM satisfait le critère 1. CQFD.
On pourra consulter le livre de David[3] (pages 8-13) pour plus de détails.
Densité de probabilité d'un vecteur aléatoire
Cette définition est en particulier valable pour d = 1 et est donc équivalente à la première définition, dans le cas particulier d = 1. Il existe une définition (équivalente) en termes d'espérance mathématique :
Théorème — Soit une variable aléatoire X à valeur dans  , de densité f, et soit φ une fonction borélienne de
, de densité f, et soit φ une fonction borélienne de  dans
dans  Alors, dès qu'un des deux termes de l'égalite suivante
Alors, dès qu'un des deux termes de l'égalite suivante
![{\displaystyle \mathbb {E} \left[\varphi (X)\right]=\int _{\mathbb {R} ^{d}}\ \varphi (u)\,f(u)\,\mathrm {d} u}](https://img.franco.wiki/i/683227ba234d9095d052f269e559f2d60de741ed.svg)
a un sens, alors l'autre aussi, et l'égalité a lieu. Réciproquement, si l'égalité ci-dessus a lieu pour tout φ borélien borné, alors f est une densité de X.
Si une fonction f est la densité de probabilité d'une variable aléatoire à valeur dans  , cette fonction vérifie les propriétés suivantes :
, cette fonction vérifie les propriétés suivantes :
- f est intégrable sur
 ;
;
 ;
;- f est presque partout positive ou nulle sur
 .
.
Réciproquement, si une fonction f vérifie les 3 propriétés ci-dessus, on peut construire une variable aléatoire X à valeur dans  ayant f pour densité de probabilité.
Les variables aléatoires qui possèdent une densité de probabilité sont appelées parfois variables à densité, parfois variables continues.
ayant f pour densité de probabilité.
Les variables aléatoires qui possèdent une densité de probabilité sont appelées parfois variables à densité, parfois variables continues.
Existence
En vertu du théorème de Radon-Nikodym, le vecteur aléatoire Z possède une densité si et seulement si, pour chaque borélien A de  dont la mesure de Lebesgue est nulle, on a
dont la mesure de Lebesgue est nulle, on a

Ce critère est rarement employé dans la pratique pour démontrer que Z possède une densité, mais il est en revanche utile pour démontrer que certaines probabilités sont nulles. Par exemple, si le vecteur aléatoire Z = (X , Y) possède une densité, alors
 ,
, ,
,
ou bien encore, plus généralement,
 ,
, ,
,
pour des fonctions φ et ψ suffisamment régulières[4], parce que la mesure de Lebesgue (c'est-à-dire la surface) de la 1re bissectrice (resp. du cercle unité, du graphe de la fonction φ, ou de la courbe d'équation ψ = 0) sont nulles.
Le critère de Radon-Nikodym peut aussi être utilisé pour démontrer qu'un vecteur aléatoire ne possède pas de densité : par exemple, si

où Θ désigne une variable aléatoire à valeur dans [0 , 2π] (par exemple, si Z est tiré au hasard uniformément sur le cercle unité, c'est-à-dire si Θ suit la loi uniforme sur [0 , 2π]), alors Z ne possède pas de densité car

Cas des variables aléatoires réelles à densité
En spécialisant à d = 1, on note que, parmi les boréliens A de  dont la mesure de Lebesgue est nulle, figurent en particulier les parties finies de
dont la mesure de Lebesgue est nulle, figurent en particulier les parties finies de  Donc une variable aléatoire réelle X à densité vérifie, en particulier :
Donc une variable aléatoire réelle X à densité vérifie, en particulier :

pour tout nombre réel x, et, par conséquent,

Il s'ensuit que les variables aléatoires réelles à densité ont nécessairement une fonction de répartition continue sur  La continuité de la fonction de répartition n'est pas, toutefois, une propriété caractéristique des variables aléatoires réelles à densité, comme le montre l'exemple de la loi de Cantor, dont la fonction de répartition est l'escalier de Cantor.
La continuité de la fonction de répartition n'est pas, toutefois, une propriété caractéristique des variables aléatoires réelles à densité, comme le montre l'exemple de la loi de Cantor, dont la fonction de répartition est l'escalier de Cantor.
Non-unicité de la densité de probabilité
Si f et g sont deux densités de probabilités de la même variable aléatoire X alors f et g sont égales presque partout. Réciproquement, si g est presque partout égale à une densité de probabilité de X, alors g est une densité de probabilité de X.
Ainsi une variable aléatoire à densité possède-t-elle toujours une infinité de densités de probabilité : par exemple, en perturbant l'une des densités de X de manière arbitraire en un nombre fini de points, on obtient encore une densité de X.
En revanche, la densité de probabilité est par conséquent unique modulo l'égalité presque partout.
Densité jointe de plusieurs variables aléatoires réelles
La fonction g définie de  dans
dans  est une densité jointe de la suite de variables aléatoires réelles (Z1, Z2, ... , Zd) si g est une densité de probabilité du vecteur aléatoire Z à valeurs dans
est une densité jointe de la suite de variables aléatoires réelles (Z1, Z2, ... , Zd) si g est une densité de probabilité du vecteur aléatoire Z à valeurs dans  défini par
défini par

On peut alors calculer la probabilité d'événements concernant les variables aléatoires réelles (Z1, Z2, ... , Zd) de la manière suivante :
Exemple :
Si d = 2,  s'écrit
s'écrit  où A désigne le demi-plan sous la première bissectrice
où A désigne le demi-plan sous la première bissectrice  On a alors, par définition de la densité,
On a alors, par définition de la densité,

Si par exemple Z1 et Z2 sont indépendants et ont même densité de probabilité f, alors une densité de Z est g = f ⊗ f, c'est-à-dire une densité de Z est g défini par g(z1, z2) = f(z1)f(z2). En ce cas,
![{\displaystyle {\begin{array}{rl}\mathbb {P} (Z_{2}\leqslant Z_{1})&=\int _{\mathbb {R} ^{2}}\,1_{z_{2}\leqslant z_{1}}f(z_{1})f(z_{2})\,\mathrm {d} z_{1}\,\mathrm {d} z_{2},\\&=\int _{\mathbb {R} }\,\left(\int _{-\infty }^{z_{1}}f(z_{2})\,\mathrm {d} z_{2}\right)f(z_{1})\,\mathrm {d} z_{1},\\&=\int _{\mathbb {R} }F(z_{1})f(z_{1})\,\mathrm {d} z_{1}\\&={\frac {1}{2}}\left[F^{2}\right]_{-\infty }^{+\infty }={\frac {1}{2}}.\end{array}}}](https://img.franco.wiki/i/85de21d29043671d3295ada1178db56ed7a6b9d8.svg)
Si par contre Z2 = Z1 p.s., le vecteur (Z1,Z2) a les mêmes lois marginales (Z1 et Z2 ont f pour densité de probabilité), mais n'a pas la même loi jointe, puisqu'alors  Ainsi la donnée des densités marginales de Z1 et Z2, seules, ne permet pas de calculer la probabilité d'événements faisant intervenir à la fois Z1 et Z2, comme l'évènement {Z2 ≤ Z1 }. Pour effectuer le calcul, on utilise ordinairement la loi jointe de Z1 et Z2, définie dans le cas ci-dessus par leur densité jointe.
Ainsi la donnée des densités marginales de Z1 et Z2, seules, ne permet pas de calculer la probabilité d'événements faisant intervenir à la fois Z1 et Z2, comme l'évènement {Z2 ≤ Z1 }. Pour effectuer le calcul, on utilise ordinairement la loi jointe de Z1 et Z2, définie dans le cas ci-dessus par leur densité jointe.
Densité marginale
Soit Z un vecteur aléatoire à valeurs dans  de densité fZ et pour ω ∈ Ω soit X(ω) et Y(ω) les deux coordonnées de Z(ω). On notera
de densité fZ et pour ω ∈ Ω soit X(ω) et Y(ω) les deux coordonnées de Z(ω). On notera

Alors
Propriété — Les variables aléatoires réelles X et Y possèdent toutes deux des densités, notons-les respectivement fX et fY, et ces densités sont données par

Les densités de probabilités fX et fY sont appelées les densités marginales de fZ.
Démonstration
Calculons ![\,{\mathbb {E}}\left[\varphi (X)\right],](https://img.franco.wiki/i/294ddb466ab05115e5f88a69b0b1c3226314159d.svg) où φ est une fonction borélienne bornée. Pour cela on peut voir φ(X) comme une fonction de Z, qu'on notera ψ(Z), où ψ = ϕ ∘ pr1 et pr1 désigne la projection sur la première coordonnée.
Alors
où φ est une fonction borélienne bornée. Pour cela on peut voir φ(X) comme une fonction de Z, qu'on notera ψ(Z), où ψ = ϕ ∘ pr1 et pr1 désigne la projection sur la première coordonnée.
Alors
![{\displaystyle {\begin{array}{rl}\mathbb {E} \left[\varphi (X)\right]&=\mathbb {E} \left[\psi (Z)\right]\\[5pt]&=\displaystyle \int _{\mathbb {R} ^{2}}\ \psi (z)\,f_{Z}(z)\,\mathrm {d} z\\[5pt]&=\displaystyle \int _{\mathbb {R} ^{2}}\ \psi (x,y)\,f_{Z}(x,y)\,\mathrm {d} x\,\mathrm {d} y\\[5pt]&=\displaystyle \int _{\mathbb {R} }\left(\int _{\mathbb {R} }\ \psi (x,y)\,f_{Z}(x,y)\,\mathrm {d} y\right)\,\mathrm {d} x\\[5pt]&=\displaystyle \int _{\mathbb {R} }\left(\int _{\mathbb {R} }\ \varphi (x)\,f_{Z}(x,y)\,\mathrm {d} y\right)\,\mathrm {d} x\\[5pt]&=\displaystyle \int _{\mathbb {R} }\varphi (x)\,\left(\int _{\mathbb {R} }\ f_{Z}(x,y)\,\mathrm {d} y\right)\,\mathrm {d} x.\end{array}}}](https://img.franco.wiki/i/9ce847b7820a66edceb988101b6d6ea628ae6b4d.svg)
Cela a lieu pour tout φ borélien borné, car ψ(Z)=φ(X) est borné donc intégrable, et ![\,{\mathbb {E}}\left[\psi (Z)\right]\](https://img.franco.wiki/i/f8d8cb2b25566c272b20f5d6f22779024239e38b.svg) est donc bien définie. En comparant le premier et le dernier terme de la série d'égalités ci-dessus, on voit que la marginale
est donc bien définie. En comparant le premier et le dernier terme de la série d'égalités ci-dessus, on voit que la marginale  satisfait la condition requise pour être une densité de probabilité de X. CQFD.
satisfait la condition requise pour être une densité de probabilité de X. CQFD.
Le cas de Y peut être traité de la même manière.
Plus généralement, si f définie de  dans
dans  est une densité jointe de :
est une densité jointe de :

on peut calculer une densité g de (par exemple) Y=(Z2, Z5, Z6) de la manière suivante (si d = 8 par exemple) :

c'est-à-dire en intégrant par rapport à toutes les coordonnées qui ne figurent pas dans le triplet Y.
La fonction g est elle aussi appelée « densité marginale » ou « marginale » de f. Une formulation générale serait lourde. La démonstration générale est calquée sur la démonstration de la propriété ci-dessus.
Densité de la médiane de 9 variables i.i.d. (ter) :
La densité jointe des 9 statistiques d'ordre[5], notées ici (Zi){1 ≤ i ≤ 9} de l'échantillon (Xi){1 ≤ i ≤ 9} est donnée par :

Par définition des statistiques d'ordre, la médiane M est aussi la 5e statistique d'ordre, Z5 On a donc :

Ainsi, de proche en proche,
![{\displaystyle {\begin{array}{rl}\displaystyle \int _{\mathbb {R} }g(z)\,\mathrm {d} z_{1}&=\displaystyle 9!\ F(z_{2})\ \prod _{i=2}^{9}f(z_{i})\ 1_{z_{2}<z_{3}<\dots <z_{9}},\\[5pt]\displaystyle \int _{\mathbb {R} ^{2}}g(z)\,\mathrm {d} z_{1}\,\mathrm {d} z_{2}&=\displaystyle {\frac {9!}{2!}}\ F(z_{3})^{2}\ \prod _{i=3}^{9}f(z_{i})\ 1_{z_{3}<\dots <z_{9}},\\[5pt]\displaystyle \int _{\mathbb {R} ^{4}}g(z)\,\mathrm {d} z_{1}\,\mathrm {d} z_{2}\,\mathrm {d} z_{3}\,\mathrm {d} z_{4}&=\displaystyle {\frac {9!}{4!}}\ F(z_{5})^{4}\ \prod _{i=5}^{9}f(z_{i})\ 1_{z_{5}<\dots <z_{9}},\\[5pt]\displaystyle \int _{\mathbb {R} ^{4}}g(z)\,\mathrm {d} z_{1}\,\mathrm {d} z_{2}\,\mathrm {d} z_{3}\,\mathrm {d} z_{4}\,\mathrm {d} z_{9}&=\displaystyle {\frac {9!}{4!\times 1!}}\ F(z_{5})^{4}\ \left(1-F(z_{8})\right)\ \prod _{i=5}^{8}f(z_{i})\ 1_{z_{5}<\dots <z_{8}},\\&\dots \\{f}_{M}(z_{5})&=\displaystyle {\frac {9!}{4!\times 4!}}F(z_{5})^{4}\left(1-F(z_{5})\right)^{4}f(z_{5}).\end{array}}}](https://img.franco.wiki/i/c53bd2c2d00b526d310f01a1f6353f25872cc205.svg)
Indépendance des variables aléatoires à densité
Soit une suite X = (X1, X2, ... ,Xn) de variables aléatoires réelles définies sur le même espace de probabilité 
Théorème —
- Si X possède une densité de probabilité
 qui s'écrit sous forme « produit » :
qui s'écrit sous forme « produit » :

- où les fonctions gi sont boréliennes et positives ou nulles, alors X est une suite de variables indépendantes. De plus, la fonction fi définie par

- est une densité de la composante Xi.
- Réciproquement, si X est une suite de variables aléatoires réelles indépendantes de densités de probabilité respectives fi alors X possède une densité de probabilité, et la fonction f définie par

- est une densité de probabilité de X.
Démonstration dans le cas de deux variables
- Sens direct
Comme la densité f est sous forme produit, on a

et par suite
![{\displaystyle {\begin{array}{rl}f(x_{1},x_{2})&=g_{1}(x_{1})\,g_{2}(x_{2})\\[3pt]&=\displaystyle {\frac {g_{1}(x_{1})}{\int _{\mathbb {R} }g_{1}(u)\,\mathrm {d} u}}\ {\frac {g_{2}(x_{2})}{\int _{\mathbb {R} }g_{2}(v)\,\mathrm {d} v}}\\&=f_{1}(x_{1})\,f_{2}(x_{2}).\end{array}}}](https://img.franco.wiki/i/1d80433a5814dc18ba7713337fd38cb2096e3738.svg)
Par construction les fonctions fi sont d'intégrale 1, donc

Ainsi les fonctions fi sont les densités de probabilités marginales des deux composantes de X. Par suite, pour tout couple de fonctions φ et ψ tel que le premier terme ci-dessous ait un sens, on a
![{\displaystyle {\begin{array}{rl}\mathbb {E} [\varphi (X_{1})\psi (X_{2})]&=\displaystyle \int \int \varphi (x_{1})\psi (x_{2})f(x_{1},x_{2})\,\mathrm {d} x_{1}\,\mathrm {d} x_{2}\\[3pt]&=\displaystyle \int \int \varphi (x_{1})f_{1}(x_{1})\psi (x_{2})f_{2}(x_{2})\,\mathrm {d} x_{1}\,\mathrm {d} x_{2}\\[3pt]&=\displaystyle \int \varphi (x_{1})f_{1}(x_{1})\,\mathrm {d} x_{1}\int \psi (x_{2})f_{2}(x_{2})\,\mathrm {d} x_{2}\\[3pt]&=\displaystyle \mathbb {E} [\varphi (X_{1})]\mathbb {E} [\psi (X_{2})]\end{array}}}](https://img.franco.wiki/i/78ed97eece13e6450ed3c1ec22b25d6f3905a551.svg)
ce qui entraine l'indépendance des variables X1 et X2.
- Sens réciproque
Il suffit de montrer que

où  est la loi de X et où μ est la mesure ayant pour densité (x1, x2) → f1(x1) f2(x2). Or
est la loi de X et où μ est la mesure ayant pour densité (x1, x2) → f1(x1) f2(x2). Or

où  est la classe des pavés boréliens :
est la classe des pavés boréliens :

En effet
![{\displaystyle {\begin{array}{rl}\mathbb {P} _{X}(A_{1}\times A_{2})&=\mathbb {P} (X_{1}\in A_{1}{\text{ et }}X_{2}\in A_{2})\\&=\mathbb {P} (X_{1}\in A_{1})\mathbb {P} (X_{2}\in A_{2})\\[3pt]&=\displaystyle \left(\int _{\mathbb {R} }1_{A_{1}}(x_{1})f_{1}(x_{1})\,\mathrm {d} x_{1}\right)\left(\int _{\mathbb {R} }1_{A_{2}}(x_{2})f_{2}(x_{2})\,\mathrm {d} x_{2}\right)\\[3pt]&=\displaystyle \int _{\mathbb {R} ^{2}}1_{A_{1}\times A_{2}}(x_{1},x_{2})f_{1}(x_{1})f_{2}(x_{2})\,\mathrm {d} x_{1}\,\mathrm {d} x_{2}\\&=\mu (A_{1}\times A_{2})\end{array}}.}](https://img.franco.wiki/i/afc043de63635544b9311843f96fd590c3ff6e45.svg)
On remarque alors que  est un π-système et que la tribu engendrée par
est un π-système et que la tribu engendrée par  est
est  donc, en vertu du lemme d'unicité des mesures de probabilités,
donc, en vertu du lemme d'unicité des mesures de probabilités,

Fonction de variables aléatoires à densité
Dans cette section, on considère la question suivante : étant donné une variable aléatoire X de densité fX et une fonction g, quelle est la loi de la variable aléatoire Y = g(X) ? En particulier, sous quelles conditions Y possède-t-elle aussi une densité de probabilité fY ? Et comment peut-on la calculer ? Une réponse rapide est que, localement, on doit pouvoir appliquer à la fonction g le théorème d'inversion locale sauf sur un ensemble de points de mesure de Lebesgue nulle). Le calcul de fY se résume alors à un changement de variable dans une intégrale simple ou multiple, comme cela est illustré dans les quelques exemples ci-dessous.
Somme de variables aléatoires indépendantes
La densité de probabilité de la somme de deux variables aléatoires indépendantes U et V, chacune ayant une densité fU et fV, est donnée par une convolution de ces densités :

Démonstration
Dans cet exemple, X =(U , V), fX(u,v) = fU(u)fV(v), g(u,v) = u + v, et Y = g(X) = U + V. Alors, pour toute fonction φ mesurable bornée,
![{\displaystyle {\begin{array}{rl}\mathbb {E} [\varphi (Y)]&=\mathbb {E} [\varphi (U+V)]=\int _{\mathbb {R} ^{2}}\varphi (u+v)f_{X}(u,v)dudv\\&=\int _{\mathbb {R} ^{2}}\varphi (y)f_{X}(t,y-t)\ |J(y,t)|\ dydt,\end{array}}}](https://img.franco.wiki/i/21d83ecc8019ad84df106b16e8ee3c60460aad3b.svg)
où J(y,t) désigne le déterminant jacobien correspondant au changement de variable

c'est-à-dire

Donc, pour toute fonction φ mesurable bornée,
![{\displaystyle {\begin{array}{rl}\mathbb {E} [\varphi (Y)]&=\int _{\mathbb {R} }\varphi (y)\left(\int _{\mathbb {R} }f_{X}(t,y-t)dt\right)\ dy\\&=\int _{\mathbb {R} }\varphi (y)\left(\int _{\mathbb {R} }f_{U}(t)f_{V}(y-t)dt\right)\ dy\\&=\int _{\mathbb {R} }\varphi (y)\ (f_{U}\ast f_{V})(y)\ dy.\end{array}}}](https://img.franco.wiki/i/a57a899d1c997acf23bb7a12d63a365ef4d10315.svg)
CQFD
Pour déterminer la loi de la somme de variables indépendantes, on peut aussi passer par la fonction génératrice des moments ou par la fonction caractéristique d'une variable aléatoire[6]. C'est ainsi qu'est démontré le théorème central limite.
La densité de probabilité de la moyenne de deux variables aléatoires indépendantes U et V, chacune ayant une densité fU et fV, s'obtient alors en utilisant la fonction suivante :

Fonction d'une variable aléatoire réelle à densité
Notons fX la densité de la variable aléatoire réelle X. Il est possible de considérer un changement de variable, dépendant de x. La transformation est la suivante : Y = g(X) où la fonction g est strictement monotone et dérivable, de dérivée qui ne s'annule nulle part. La densité fY(y) de la transformée est
Théorème — 
où g−1 représente la fonction réciproque de g et g' la dérivée de g.
Démonstration
Ce résultat découle du fait que les probabilités sont invariantes par changement de variable. Supposons par exemple que g est décroissante :

En différenciant, on obtient

qui s'écrit encore

Le cas où g est croissante se traite de manière analogue.
Pour une transformation g non monotone, la densité de probabilité de Y est

où n(y) est le nombre de solutions en x de l'équation g(x) = y, et g-1
k(y) sont les solutions. La fonction g doit vérifier certaines hypothèses, toutefois : essentiellement on doit pouvoir lui appliquer le théorème d'inversion locale sauf sur un ensemble de points de mesure de Lebesgue nulle. Par exemple un ensemble d'hypothèses peu limitatif mais simple à vérifier serait : g est de classe C1 et l'ensemble des zéros de la dérivée g' est localement fini. Il s'agit d'exclure entre autres (mais pas seulement) le cas où g est constante sur un ensemble de mesure non nulle pour la loi de X, cas où g(X) n'a pas une loi à densité, car la loi de g(X) peut alors avoir une partie discrète.
Exemples :

- En effet, si, par exemple, a est strictement négatif, on obtient, via le changement de variable u = ax + b
![{\displaystyle {\begin{array}{cl}\mathbb {E} [\varphi (Y)]&=\displaystyle \mathbb {E} [\varphi (aX+b)]=\int _{\mathbb {R} }\varphi (ax+b)f_{X}(x)\,\mathrm {d} x\\[7pt]&=\displaystyle \int _{+\infty }^{-\infty }\varphi (u)f_{X}\left({\frac {u-b}{a}}\right)\ {\frac {\mathrm {d} u}{a}}\\[7pt]&=\displaystyle \int _{-\infty }^{+\infty }\varphi (u)\ \left({\frac {1}{-a}}\ f_{X}\left({\frac {u-b}{a}}\right)\right)\,\mathrm {d} u,\end{array}}}](https://img.franco.wiki/i/8306969f4be101311035ab14e06357315322aba1.svg)
- ceci pour toute fonction φ mesurable bornée. CQFD.
- Prenons l'exemple du carré d'une variable aléatoire ; on sait que, si Y = X2
![{\displaystyle {\begin{array}{rl}\mathbb {E} [\varphi (Y)]&=\displaystyle \mathbb {E} [\varphi (X^{2})]=\int _{\mathbb {R} }\varphi (x^{2})f_{X}(x)\,\mathrm {d} x\\[7pt]&=\displaystyle \int _{-\infty }^{0}\varphi (x^{2})f_{X}(x)\,\mathrm {d} x+\int _{0}^{+\infty }\varphi (x^{2})f_{X}(x)\,\mathrm {d} x\\[7pt]&=\displaystyle \int _{+\infty }^{0}\varphi (u)f_{X}(-{\sqrt {u}})\ \left(-{\frac {\mathrm {d} u}{2{\sqrt {u}}}}\right)+\int _{0}^{+\infty }\varphi (u)f_{X}({\sqrt {u}})\ \left({\frac {\mathrm {d} u}{2{\sqrt {u}}}}\right)\\[7pt]&=\displaystyle \int _{\mathbb {R} }\varphi (u)\ {\frac {1}{2{\sqrt {u}}}}\left[f_{X}({\sqrt {u}})+f_{X}(-{\sqrt {u}})\right]1_{\mathbb {R} _{+}}(u)\,\mathrm {d} u,\end{array}}}](https://img.franco.wiki/i/3be6f405873155a498db40df7e00c1447c7eac89.svg)
- ceci pour toute fonction φ mesurable bornée. Ainsi, on trouve que
![f_{Y}(y)={\frac {1}{2{\sqrt {y}}}}\left[f_{X}({\sqrt {y}})+f_{X}(-{\sqrt {y}})\right]1_{{{\mathbb {R}}_{+}}}(y)](https://img.franco.wiki/i/4ef71191ace0199850683f0ebab3a7ea02be509f.svg)
- ce qui est conforme à la formule.
- Autre solution : on sait que,


- En dérivant, on trouve à nouveau
![f_{Y}(y)={\frac {1}{2{\sqrt {y}}}}\left[f_{X}({\sqrt {y}})+f_{X}(-{\sqrt {y}})\right]1_{{{\mathbb {R}}_{+}}}(y).](https://img.franco.wiki/i/60eade58e6ea1f7cddfdbf6c309e42b49af926c7.svg)
Contre-exemple :
Prenons X uniforme sur [0 ; 2] et g(x) = min (x,1). Alors
![{\displaystyle \mathbb {P} _{Y}(\mathrm {d} y)={\tfrac {1}{2}}\ 1_{[0;1]}(y)\,\mathrm {d} y\ +\ {\tfrac {1}{2}}\ \delta _{1}(\mathrm {d} y).}](https://img.franco.wiki/i/54203ac5ec465b2797d034a13230bc1ca0947624.svg)
Autrement dit, la loi de Y a une partie à densité, mais aussi un atome en 1.























![{\displaystyle {\begin{array}{rl}\mathbb {P} \left(M\leq t\right)&=F_{M}(t)=\mathbb {P} \left({\text{au moins 5 des 9 }}X_{i}{\text{ sont }}\leq t\right)\\[5pt]&={\displaystyle \sum _{j=5}^{9}{9 \choose j}F(t)^{j}(1-F(t))^{9-j}.}\end{array}}}](https://img.franco.wiki/i/23d866de48c73c8f7a0f939561acffa0d0ed54e5.svg)








![{\displaystyle \mathbb {E} \left[\varphi (X)\right]=\int _{\mathbb {R} ^{d}}\ \varphi (u)\,f(u)\,\mathrm {d} u}](https://img.franco.wiki/i/683227ba234d9095d052f269e559f2d60de741ed.svg)


















![{\displaystyle {\begin{array}{rl}\mathbb {P} (Z_{2}\leqslant Z_{1})&=\int _{\mathbb {R} ^{2}}\,1_{z_{2}\leqslant z_{1}}f(z_{1})f(z_{2})\,\mathrm {d} z_{1}\,\mathrm {d} z_{2},\\&=\int _{\mathbb {R} }\,\left(\int _{-\infty }^{z_{1}}f(z_{2})\,\mathrm {d} z_{2}\right)f(z_{1})\,\mathrm {d} z_{1},\\&=\int _{\mathbb {R} }F(z_{1})f(z_{1})\,\mathrm {d} z_{1}\\&={\frac {1}{2}}\left[F^{2}\right]_{-\infty }^{+\infty }={\frac {1}{2}}.\end{array}}}](https://img.franco.wiki/i/85de21d29043671d3295ada1178db56ed7a6b9d8.svg)




![\,{\mathbb {E}}\left[\varphi (X)\right],](https://img.franco.wiki/i/294ddb466ab05115e5f88a69b0b1c3226314159d.svg)
![{\displaystyle {\begin{array}{rl}\mathbb {E} \left[\varphi (X)\right]&=\mathbb {E} \left[\psi (Z)\right]\\[5pt]&=\displaystyle \int _{\mathbb {R} ^{2}}\ \psi (z)\,f_{Z}(z)\,\mathrm {d} z\\[5pt]&=\displaystyle \int _{\mathbb {R} ^{2}}\ \psi (x,y)\,f_{Z}(x,y)\,\mathrm {d} x\,\mathrm {d} y\\[5pt]&=\displaystyle \int _{\mathbb {R} }\left(\int _{\mathbb {R} }\ \psi (x,y)\,f_{Z}(x,y)\,\mathrm {d} y\right)\,\mathrm {d} x\\[5pt]&=\displaystyle \int _{\mathbb {R} }\left(\int _{\mathbb {R} }\ \varphi (x)\,f_{Z}(x,y)\,\mathrm {d} y\right)\,\mathrm {d} x\\[5pt]&=\displaystyle \int _{\mathbb {R} }\varphi (x)\,\left(\int _{\mathbb {R} }\ f_{Z}(x,y)\,\mathrm {d} y\right)\,\mathrm {d} x.\end{array}}}](https://img.franco.wiki/i/9ce847b7820a66edceb988101b6d6ea628ae6b4d.svg)
![\,{\mathbb {E}}\left[\psi (Z)\right]\](https://img.franco.wiki/i/f8d8cb2b25566c272b20f5d6f22779024239e38b.svg)





![{\displaystyle {\begin{array}{rl}\displaystyle \int _{\mathbb {R} }g(z)\,\mathrm {d} z_{1}&=\displaystyle 9!\ F(z_{2})\ \prod _{i=2}^{9}f(z_{i})\ 1_{z_{2}<z_{3}<\dots <z_{9}},\\[5pt]\displaystyle \int _{\mathbb {R} ^{2}}g(z)\,\mathrm {d} z_{1}\,\mathrm {d} z_{2}&=\displaystyle {\frac {9!}{2!}}\ F(z_{3})^{2}\ \prod _{i=3}^{9}f(z_{i})\ 1_{z_{3}<\dots <z_{9}},\\[5pt]\displaystyle \int _{\mathbb {R} ^{4}}g(z)\,\mathrm {d} z_{1}\,\mathrm {d} z_{2}\,\mathrm {d} z_{3}\,\mathrm {d} z_{4}&=\displaystyle {\frac {9!}{4!}}\ F(z_{5})^{4}\ \prod _{i=5}^{9}f(z_{i})\ 1_{z_{5}<\dots <z_{9}},\\[5pt]\displaystyle \int _{\mathbb {R} ^{4}}g(z)\,\mathrm {d} z_{1}\,\mathrm {d} z_{2}\,\mathrm {d} z_{3}\,\mathrm {d} z_{4}\,\mathrm {d} z_{9}&=\displaystyle {\frac {9!}{4!\times 1!}}\ F(z_{5})^{4}\ \left(1-F(z_{8})\right)\ \prod _{i=5}^{8}f(z_{i})\ 1_{z_{5}<\dots <z_{8}},\\&\dots \\{f}_{M}(z_{5})&=\displaystyle {\frac {9!}{4!\times 4!}}F(z_{5})^{4}\left(1-F(z_{5})\right)^{4}f(z_{5}).\end{array}}}](https://img.franco.wiki/i/c53bd2c2d00b526d310f01a1f6353f25872cc205.svg)






![{\displaystyle {\begin{array}{rl}f(x_{1},x_{2})&=g_{1}(x_{1})\,g_{2}(x_{2})\\[3pt]&=\displaystyle {\frac {g_{1}(x_{1})}{\int _{\mathbb {R} }g_{1}(u)\,\mathrm {d} u}}\ {\frac {g_{2}(x_{2})}{\int _{\mathbb {R} }g_{2}(v)\,\mathrm {d} v}}\\&=f_{1}(x_{1})\,f_{2}(x_{2}).\end{array}}}](https://img.franco.wiki/i/1d80433a5814dc18ba7713337fd38cb2096e3738.svg)

![{\displaystyle {\begin{array}{rl}\mathbb {E} [\varphi (X_{1})\psi (X_{2})]&=\displaystyle \int \int \varphi (x_{1})\psi (x_{2})f(x_{1},x_{2})\,\mathrm {d} x_{1}\,\mathrm {d} x_{2}\\[3pt]&=\displaystyle \int \int \varphi (x_{1})f_{1}(x_{1})\psi (x_{2})f_{2}(x_{2})\,\mathrm {d} x_{1}\,\mathrm {d} x_{2}\\[3pt]&=\displaystyle \int \varphi (x_{1})f_{1}(x_{1})\,\mathrm {d} x_{1}\int \psi (x_{2})f_{2}(x_{2})\,\mathrm {d} x_{2}\\[3pt]&=\displaystyle \mathbb {E} [\varphi (X_{1})]\mathbb {E} [\psi (X_{2})]\end{array}}}](https://img.franco.wiki/i/78ed97eece13e6450ed3c1ec22b25d6f3905a551.svg)





![{\displaystyle {\begin{array}{rl}\mathbb {P} _{X}(A_{1}\times A_{2})&=\mathbb {P} (X_{1}\in A_{1}{\text{ et }}X_{2}\in A_{2})\\&=\mathbb {P} (X_{1}\in A_{1})\mathbb {P} (X_{2}\in A_{2})\\[3pt]&=\displaystyle \left(\int _{\mathbb {R} }1_{A_{1}}(x_{1})f_{1}(x_{1})\,\mathrm {d} x_{1}\right)\left(\int _{\mathbb {R} }1_{A_{2}}(x_{2})f_{2}(x_{2})\,\mathrm {d} x_{2}\right)\\[3pt]&=\displaystyle \int _{\mathbb {R} ^{2}}1_{A_{1}\times A_{2}}(x_{1},x_{2})f_{1}(x_{1})f_{2}(x_{2})\,\mathrm {d} x_{1}\,\mathrm {d} x_{2}\\&=\mu (A_{1}\times A_{2})\end{array}}.}](https://img.franco.wiki/i/afc043de63635544b9311843f96fd590c3ff6e45.svg)



![{\displaystyle {\begin{array}{rl}\mathbb {E} [\varphi (Y)]&=\mathbb {E} [\varphi (U+V)]=\int _{\mathbb {R} ^{2}}\varphi (u+v)f_{X}(u,v)dudv\\&=\int _{\mathbb {R} ^{2}}\varphi (y)f_{X}(t,y-t)\ |J(y,t)|\ dydt,\end{array}}}](https://img.franco.wiki/i/21d83ecc8019ad84df106b16e8ee3c60460aad3b.svg)


![{\displaystyle {\begin{array}{rl}\mathbb {E} [\varphi (Y)]&=\int _{\mathbb {R} }\varphi (y)\left(\int _{\mathbb {R} }f_{X}(t,y-t)dt\right)\ dy\\&=\int _{\mathbb {R} }\varphi (y)\left(\int _{\mathbb {R} }f_{U}(t)f_{V}(y-t)dt\right)\ dy\\&=\int _{\mathbb {R} }\varphi (y)\ (f_{U}\ast f_{V})(y)\ dy.\end{array}}}](https://img.franco.wiki/i/a57a899d1c997acf23bb7a12d63a365ef4d10315.svg)







![{\displaystyle {\begin{array}{cl}\mathbb {E} [\varphi (Y)]&=\displaystyle \mathbb {E} [\varphi (aX+b)]=\int _{\mathbb {R} }\varphi (ax+b)f_{X}(x)\,\mathrm {d} x\\[7pt]&=\displaystyle \int _{+\infty }^{-\infty }\varphi (u)f_{X}\left({\frac {u-b}{a}}\right)\ {\frac {\mathrm {d} u}{a}}\\[7pt]&=\displaystyle \int _{-\infty }^{+\infty }\varphi (u)\ \left({\frac {1}{-a}}\ f_{X}\left({\frac {u-b}{a}}\right)\right)\,\mathrm {d} u,\end{array}}}](https://img.franco.wiki/i/8306969f4be101311035ab14e06357315322aba1.svg)
![{\displaystyle {\begin{array}{rl}\mathbb {E} [\varphi (Y)]&=\displaystyle \mathbb {E} [\varphi (X^{2})]=\int _{\mathbb {R} }\varphi (x^{2})f_{X}(x)\,\mathrm {d} x\\[7pt]&=\displaystyle \int _{-\infty }^{0}\varphi (x^{2})f_{X}(x)\,\mathrm {d} x+\int _{0}^{+\infty }\varphi (x^{2})f_{X}(x)\,\mathrm {d} x\\[7pt]&=\displaystyle \int _{+\infty }^{0}\varphi (u)f_{X}(-{\sqrt {u}})\ \left(-{\frac {\mathrm {d} u}{2{\sqrt {u}}}}\right)+\int _{0}^{+\infty }\varphi (u)f_{X}({\sqrt {u}})\ \left({\frac {\mathrm {d} u}{2{\sqrt {u}}}}\right)\\[7pt]&=\displaystyle \int _{\mathbb {R} }\varphi (u)\ {\frac {1}{2{\sqrt {u}}}}\left[f_{X}({\sqrt {u}})+f_{X}(-{\sqrt {u}})\right]1_{\mathbb {R} _{+}}(u)\,\mathrm {d} u,\end{array}}}](https://img.franco.wiki/i/3be6f405873155a498db40df7e00c1447c7eac89.svg)
![f_{Y}(y)={\frac {1}{2{\sqrt {y}}}}\left[f_{X}({\sqrt {y}})+f_{X}(-{\sqrt {y}})\right]1_{{{\mathbb {R}}_{+}}}(y)](https://img.franco.wiki/i/4ef71191ace0199850683f0ebab3a7ea02be509f.svg)


![f_{Y}(y)={\frac {1}{2{\sqrt {y}}}}\left[f_{X}({\sqrt {y}})+f_{X}(-{\sqrt {y}})\right]1_{{{\mathbb {R}}_{+}}}(y).](https://img.franco.wiki/i/60eade58e6ea1f7cddfdbf6c309e42b49af926c7.svg)
![{\displaystyle \mathbb {P} _{Y}(\mathrm {d} y)={\tfrac {1}{2}}\ 1_{[0;1]}(y)\,\mathrm {d} y\ +\ {\tfrac {1}{2}}\ \delta _{1}(\mathrm {d} y).}](https://img.franco.wiki/i/54203ac5ec465b2797d034a13230bc1ca0947624.svg)