1 − 2 + 3 − 4 + ···

رسم توضيحي يظهر أول 15000 مجموع جزئي من سلسلة 0 + 1 − 2 + 3 − 4 + · · ·، وتظهر الأرقام الموجبة إلى اليمين والأرقام السالبة إلى اليسار.

في الرياضيات، تشير صيغة 1 − 2 + 3 − 4 + ··· إلى متسلسة غير منتهية والتي تكون حدودها أعداد صحيحة موجبة ذات إشارة متناوبة.^[1] وباستخدام صيغة مجموع سيغما، يكون مجموع الحدود m الأولى من هذه المتسلسة معطى بالعلاقة :

${\displaystyle \sum _{n=1}^{m}n(-1)^{n-1}}$

هذه المتسلسلة هي متسلسلة متباعدة، لأن المجاميع الجزئية لهذه المتسلسلة (1، -1، 2، -2، ...) لا تؤول إلى قيمة محدودة. على الرغم من ذلك فإن أويلر كتب في القرن الثامن عشر مفارقة تنص بأن المجموع الكلي لهذه المتسلسة هو 1/4 بالشكل :

${\displaystyle 1-2+3-4+\cdots ={\frac {1}{4}}}$

وظلت تلك المفارقة بدون إثبات لمدة طويلة. ومنذ عام 1890، قام إرنست سيزارو و إيميل بوريل وآخرون بدراسة طرق محددة لتعيين مجاميع عامة للمتسلسلات المتباعدة تتضمن تفسيرات جديدة لمحاولة أويلر. الكثير من تلك الطرق تحقق أن مجموع متسلسلة 1 − 2 + 3 − 4 + ... هو القيمة ¹⁄₄. كانت طريقة "مجموع سيزارو" من الطرق القلائل التي لم تعطي مجموعا لمتسلسلة 1 − 2 + 3 − 4 + ...، ولذلك تعد هذه المتسلسلة مثالا على المتسلسلات التي تحتاج إلى طريقة أقوى مثل مجموع آبل.

متسلسلة 1 − 2 + 3 − 4 + ... مرتبطة ب متسلسلة غراندي 1 − 1 + 1 − 1 + .... تعامل أويلر مع هاتين المتسلسلتين كحالة خاصة من ( 1 − 2ⁿ + 3ⁿ − 4ⁿ + ...) لقيم اختيارية للمتغير n، وهناك أبحاث لتعميم عمله على معضلة بازل تؤدي إلى معادلة دالية لما يُعرف بـ دالة إيتا لدركليه و دالة زيتا لريمان.

التباعد

حدود المتسلسلة (1, −2, 3, −4, ...) لا تؤول إلى 0، وبالتالي فإن 1 − 2 + 3 − 4 + ... تتباعد وفق اختبار الحد النوني. وفقا للتعريف فإن تقارب أو تباعد متسلسلة محدودة يمكن تحديده من  تقارب أو تباعد مجاميعها الجزئية. المجاميع الجزئية لـ 1 − 2 + 3 − 4 + ... هي:^[2]

1 = 1,

1 − 2 = −1,

1 − 2 + 3 = 2,

1 − 2 + 3 − 4 = −2,

1 − 2 + 3 − 4 + 5 = 3,

1 − 2 + 3 − 4 + 5 − 6 = −3,

...

يُلاحظ أن كل عدد صحيح (Integer) يظهر مرة واحدة فقط، حتى الـ0 في حالة المجموع الجزئي الفارغ ( empty partial sum) وبالتالي فهو مجموعة قابلة للعد للمجموعة ${\displaystyle \mathbb {Z} }$ (أعداد صحيحة).^[3] متتالية المجاميع الجزئية توضح أن المتسلسلة لا تتقارب إلى رقمٍ ما (لأي نهاية مفترضة x، يمكن إيجاد نقطة تالية بحيث أن المجاميع الجزئية التالية لها تقع جميعها خارج الفترة [x−1, x+1])، لذلك فإن المتسلسلة 1 − 2 + 3 − 4 + ... متباعدة.

الاستدلال على الجمع

الاستقرار والخطية

حيث أن العناصر 1, −2, 3, −4, 5, −6, ... تتبع نظام بسيط، فإن المتسلسلة 1 − 2 + 3 − 4 + ... يمكن التعامل معها بإزاحة العناصر واحدا واحدا ثم الجمع لإيجاد قيمة لها. إذا قلنا أن ... + s = 1 − 2 + 3 − 4 ، فالطريقة التالية توضح أن  s = ¹⁄₄ : ^[4]

${\displaystyle {\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+(1-2)+(3-4+5-6\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}-1+(3-4+5-6\cdots )\\&=&1+&(1-2+3-4+\cdots )&{}+(-2+3-4+5+\cdots )&{}+(-2+3-4+5+\cdots )&{}+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&{}+(-2+3+3-4)&{}+(3-4-4+5)&{}+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}}$

بجمع 4 نسخ من 1 − 2 + 3 − 4 + ..., بعد عمل إزاحة والجمع ينتج 1. كل واحدة من الناحيتين اليمين واليسار تبين جمع نسختين من 1 − 2 + 3 − 4 + ... لاحظ أن ناتج الجمع هو 1 − 1 + 1 − 1 + ....

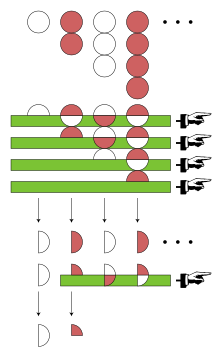
أي أن  ${\displaystyle s={\frac {1}{4}}}$. ويمكن توضيح ذلك بالرسم المقابل.

رغم أن 1 − 2 + 3 − 4 + ... ليس لها مجموع بمجرد النظر، إلا أن s = 1 − 2 + 3 − 4 + ... = ¹⁄₄  يمكن دعمها إذا أردنا تعريف ذلك المجموع. هناك العديد من الطرق (بعضها مذكور أدناه) للتعامل مع مجموع متسلسلة متباعدة. ومن المفضل لتلك الطرق أن يكون لها بعض خصائص جمع المتسلسلات العادية. وباستخدام أية طريقة للجمع (خطية ومستقرة) فإن مجموع  1 − 2 + 3 − 4 + ... هو ¹⁄₄.^[5]

وحيث أن:

${\displaystyle {\begin{array}{rcllll}2s&=&&(1-2+3-4+\cdots )&+&(1-2+3-4+\cdots )\\&=&1+{}&(-2+3-4+\cdots )&{}+1-2&{}+(3-4+5\cdots )\\&=&0+{}&(-2+3)+(3-4)+(-4+5)+\cdots \\2s&=&&1-1+1-1\cdots \end{array}}}$

فهذه الطريقة يمكن استخدامها لإثبات أن مجموع متسلسلة غراندي 1 − 1 + 1 − 1 + ... = ¹⁄₂.^[5]

مضروب كوشي

في عام 1891، أعطى إيرنست سيزارو أملا في إيجاد حلولا رياضية للمتسلسلات المتباعدة، فمثلا (1 − 1 + 1 − 1 + ...)² = 1 − 2 + 3 − 4 + ... وكلا الطرفان يساوي ¹⁄₄.^[6] وكان ذلك تطبيقا لنظرية نشرها سيزارو في العام السابق، والتي تُعد أول نظرية في التاريخ لجمع المتسلسلات المتباعدة.^[7] وبيان ذلك الجمع كالتالي:  الفكرة المحورية هي أن 1 − 2 + 3 − 4 + ... هي مضروب كوشي (التفاف رقمي) لكلا من 1 − 1 + 1 − 1 + ... مع 1 − 1 + 1 − 1 + ....

يمكن تعريف مضروب كوشي لمتسلسلتين لا نهائيتين حتى لو كانت كلتاهما متباعدة. ففي حالة ما إذا كان a_n = b_n = (−1)ⁿ، فإن عناصر مضروب كوشي تُعطى بمجموع الأقطار المحدود

${\displaystyle {\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}}$

وبالتالي فإن متسلسلة الضرب هي:

${\displaystyle \sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .}$

فطريقة الجمع التي توافق مضروب كوشي لمتسلسلتين، والتي أثبتت أن مجموع المتسلسلة 1 − 1 + 1 − 1 + ...هو 1/2 يمكنها أيضا أن تثبت أن مجموع المتسلسلة 1 − 2 + 3 − 4 + ... هو 1/4. مما سبق فهناك توافق بين طرق جمع 1 − 1 + 1 − 1 + ... و 1 − 2 + 3 − 4 + ... مع الطرق الخطية المستقرة التي تحقق مضروب كوشي.

وتعد نظرية سيزارو مثالا واضحا لذلك. المتسلسلة 1 − 1 + 1 − 1 + ... قابلة للجمع (وفق سيزارو) بأقل درجة، وتسمى قابلة للجمع-(C, 1) بينما المتسلسلة 1 − 2 + 3 − 4 + ... تحتاج شكل أقوى من نظريات سيزارو،^[8]  هي قابلة للجمع-(C, 2). وحيث أن كل أشكال نظرية سيزارو هي خطية ومستقرة، فإن نتائج الجمع هي كما أسلفنا.

طرق خاصة

سيزارو وهولدر

بيانات عن مجموع (H, 2)  والناتج  ¹⁄₄

لإيجاد مجموع سيزارو(C, 1) للمتسلسلة 1 − 2 + 3 − 4 + ...، إذا كان موجودا، يجب حساب المتوسطات الحسابية للمجاميع الجزئية للمتسلسلة. المجاميع الجزئية هي:

1 ، −1 ، 2 ، −2 ، 3 ، −3 ، ...،

والمتوسطات الحسابية لتلك المجاميع الجزئية هي:

1 ، 0 ، ²⁄₃، 0 ، ³⁄₅، 0 ، ⁴⁄₇، ....

وهذه المتوسطات لا تتقارب، ولذلك فالمتسلسلة   1 − 2 + 3 − 4 + ... ليست قابلة للجمع وفق سيزارو.

هناك تعميمان مشهوران لجمع سيزارو: أبسطهما هو طرق (H, n) للأعداد الطبيعية n. حيث (H, 1) هو مجموع سيزارو، والطرق الأعلى تُكرر حساب المتوسطات. كما نرى -أعلاه- فإن المتوسطات الزوجية تتقارب إلى ¹⁄₂، بينما المتوسطات الفردية جميعها يساوي 0، وبذلك يكون متوسط المتوسطات يتقارب إلى 0  و ¹⁄₂، أي ¹⁄₄.^[9] وبالتالي يمكن القول أن 1 − 2 + 3 − 4 + ... هي قابلة للجمع(H, 2) وتؤول إلى ¹⁄₄.

الرمز "H" يعود للعالِم Otto Hölder، والذي يُعد أول من أثبت في عام 1882 ما يعتبره الرياضاتيون الآن الرابط بين "مجموع آبل" ومجموع (H, n); المتسلسلة  1 − 2 + 3 − 4 + ... كانت أول مثال.^[10] حقيقة أن ¹⁄₄ هي مجموع (H, 2) للمتسلسلة 1 − 2 + 3 − 4 + ... أكدت أنها هي "مجموع آبل" أيضا، وسيتم أثبات ذلك لاحقا.

التعميم الآخر لجمع سيزارو هو طرق (C, n). حيث ثبت أن جمع (C, n) وجمع (H, n) دائما يعطيان نفس النتائج، لكن لهما خلفيات مختلفة. في عام 1887، اقترب سيزارو من وضع تعريف جمع (C, n) ، لكنه أعطى أمثلة قليلة. فقد ذكر أن مجموع المتسلسلة 1 − 2 + 3 − 4 + ...، هو القيمة ¹⁄₄ بطريقة يمكن اعتبارها قريبة من طريقة جمع (C, n) لكنها لم يتم تحقيقها في ذلك الوقت. وقد قام بصياغة طريقة جمع (C, n) في عام 1890 لينص على أن مضروب كوشي لمتسلسة قابلة للجمع-(C, n) ومتسلسلة قابلة للجمع-(C, m) هو متسلسلة قاببة للجمع- (C, m + n + 1).^[11]

مجموع آبل

في عام 1749، قرر أويلر أن المتسلسلة تتباعد لكنه حاول إيجاد مجموع لها بأية طريقة:

قدَّم أويلر عدة تعميمات لكلمة "جمع". في حالة المتسلسلة  1 − 2 + 3 − 4 + ...تُعد فكرته مشابهة لما يُعرف بـ "مجموع آبل":

ليس هناك شك في أن مجموع المتسلسلة 1 − 2 + 3 − 4 + 5 هو 1⁄4، لأنها تأتي من مفكوك المعادلة ${\displaystyle {\frac {1}{(1+1)^{2}}}.}$ والتي قيمتها 1⁄4. ويمكن توضيح الفكرة باعتبار المتسلسلة العامة (${\displaystyle 1-2x+3x^{2}-4x^{3}+\cdots }$). والتي تظهر في مفكوك ${\displaystyle {\frac {1}{(1+x)^{2}}}.}$، الذي يساوي هذه المتسلسلة عندما نضع x = 1.^[13]

هناك طرق عديدة لبيان ذلك، على الأقل للقيم المطلقة ${\displaystyle |x|<1.}$، فإن أويلر على صواب في ذلك:

${\displaystyle 1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}.}$

يمكن إيجاد مفكوك تايلور للجانب الأيمن من المعادلة أو تطبيق طريقة القسمة المطولة لكثيرات الحدود. بدءاً بالجانب الأيسر، يمكن متابعة الحل أعلاه ويمكن الضرب في (1 + x) مرتين أو تربيع المتسلسلة الهندسية ${\displaystyle 1-x+x^{2}-\cdots }$. اقترح أويلر أيضا اشتقاق المتسلسلة الأخيرة عنصرا عنصرا.^[14]

وفقا للنظرة الحديثة فإن المتسلسلة ${\displaystyle 1-2x+3x^{2}-4x^{3}\cdots }$ ليست مُعرفة كدالة عند  x = 1، وبالتالي لا يمكن التعويض بهذه القيمة في تلك العلاقة. وحيث أن الدالة مُعرفة عند كل ${\displaystyle |x|<1.}$، يمكننا أخذ النهاية عندما x تؤول إلى 1، وهذا هو تعريف "مجموع آبل":

${\displaystyle \lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.}$

أويلر وبوريل

مجموع أويلر لـ ¹⁄₂ − ¹⁄₄

طبق أولير طريقة أخرى على تلك المتسلسلة: تحويل أويلر هو واحد من ابتكاراته، ولحساب تحويل أويلر نبدأ بالحدود الموجبة للمتسلسلة وهي 1 ، 2 ، 3 ، 4 ، .... ونعطي التسمية a₀ للعنصر الأول.

ثم نحسب الفروق المحدودة (forward differences) لهذه الأرقام 1 ، 2 ، 3 ، 4 ، ...، والتي هي 1 ، 1 ، 1 ، 1 ، .... نسمي أول عنصر منها Δa₀. يعتمد تحويل أويلر على "فروق الفروق"، لكن كل الفروق لـ 1 ، 1 ، 1 ، 1 ، ... هي 0. وبالتالي فإن تحويل أويلر لـ 1 − 2 + 3 − 4 + ... يمكن تعريفه أنه:

${\displaystyle {\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}.}$

أو يمكن القول أن 1 − 2 + 3 − 4 + ... قابلة للجمع "وفق أويلر" وقيمتها ¹⁄₄.

قابلية الجمع عند أويلر تتضمن أن 1 − 2 + 3 − 4 + ... هو 

${\displaystyle \sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1),}$

وهي المعادلة المرتبطة بالمتسلسلات المتقاربة

${\displaystyle a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k+1}}{(k+1)!}}=x\sum _{k=0}^{\infty }{\frac {(-x)^{k}}{k!}}=e^{-x}x.}$

"مجموع بوريل" للمتسلسلة  1 − 2 + 3 − 4 + ...هو:^[15]

${\displaystyle \int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}x\,dx=-{\frac {\partial }{\partial \beta }}{\bigg |}_{2}\int _{0}^{\infty }e^{-\beta x}\,dx=-{\frac {\partial }{\partial \beta }}{\bigg |}_{2}\beta ^{-1}={\frac {1}{4}}.}$

فصل المقاييس Separation of scales

توصل سيتشيف وويكشينسكي إلى أن 1 − 2 + 3 − 4 + ... = ¹⁄₄ بتطبيق مبدأين فقط هما: (infinitesimal relaxation) و (separation of scales). وكان هذان المبدأن سببا لتعريف طرق عديدة أطلقا عليها اسم ("φ-summation methods")، وجميعها أعطى نفس النتيجة بأن مجموع هذه المتسلسلة هو ¹⁄₄:

• إذا كان (φ(x هي دالة بحيث أن المشتقتين الأولى والثانية لها متصلتان وقابلتان للتكامل على الفترة (0, ∞)، بحيث أن φ(0) = 1 ونهايات (φ( x و (xφ(x عند +∞ هي 0، فإن^[16]

${\displaystyle \lim _{\delta \rightarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}.}$

هذه النتيجة تعتبر تعميم لمجموع آبل، والذي يمكن الحصول عليه عند تساوي كلا من (φ(x و (exp(-x. ويمكن إثبات هذا التعميم بأخذ أزواج من عناصر المتسلسلة على m وتحويلها إلى تكامل ريمان. وفق الخطوة الأخيرة فإن الإثبات المناظر لمتسلسلة غراندي 1 − 1 + 1 − 1 + ... يُطبق مبرهنة القيمة الوسطى، لكننا نحتاج صيغة لاجرانج الأقوى من مبرهنة تايلور.

تعميم

Excerpt from p.233 of the E212 — Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum. Euler sums similar series, ca. 1755.

مضروب كوشي الثلاثي (threefold) للمتسلسلة 1 − 1 + 1 − 1 + ... هو 1 − 3 + 6 − 10 + ...، وهي متسلسلة مترددة من الأعداد المثلثية، والتي مجموعها وفق "آبل" و "أويلر" هو ¹⁄₈.^[17] مضروب كوشي الرباعي (fourfold)  لـ 1 − 1 + 1 − 1 + ... هو 1 − 4 + 10 − 20 + ...، وهي متسلسلة مترددة من الأعداد الهرمية الثلاثية. ومجموع آبل لها هو ¹⁄₁₆.

تعميم آخر للمتسلسلة 1 − 2 + 3 − 4 + ... بطريقة أخرى للمتسلسلة ${\displaystyle 1-2^{n}+3^{n}-\cdots }$ لقيم أخرى لـ n.

لقيم n الصحيحة، يكون لهذه المتسلسة مجاميع آبل التالية:^[18]

${\displaystyle 1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}}$

حيث B_n هي أعداد بيرنولي.

لقيم n الزوجية، يُختصر ذلك إلى

${\displaystyle 1-2^{2k}+3^{2k}-\cdots =0.}$

وهذا المجموع الأخير كان مثارا للسخرية من آبل في عام  1826، حيث قال: المتسلسلات المتباعدة هي من عمل الشيطان، وإنه لمن العار أن يجرؤ أحد للبحث عن إثبات لها. يمكن للمرء أن يُخرج منها ما يريده إذا استخدمهم، وهي التي تجلب الكثير من التعاسة والكثير من المفارقات. هل يمكن للمرء أن يفكر في أي شيء أكثر رعبا من القول بأن ${\displaystyle 1-2^{n}+3^{n}-\cdots =0}$، حيث n هو رقم موجب. إنه شيء يدعو للضحك يا أصدقائي.^[19]

كان أوجين شارل كاتالان، مُعلم سيزارو، يستخف بالمتسلسلة المتباعدة. وبتأثير كاتالان، أشار سيزارو في البداية إلى "الصيغ التقليدية" للمتسلسلة ${\displaystyle 1-2^{n}+3^{n}-\cdots }$ هي "معادلات سخيفة"، وفي عام 1883 أعرب سيزارو عن وجهة نظر نموذجية لذلك الوقت بأن تلك الصيغ كانت خطأ ولكنها لا تزال بطريقة أو بأخرى مفيدة رسميا. وأخيرا، في عام 1890، اتخذ سيزارو نهجا حديثا بدءا من التعاريف، وقام بنشره في (Sur la multiplication des séries).^[20]

تم دراسة المتسلسلات لقيم n غير الصحيحة، فنتج عنها دالة إيتا لدركليه. كانت المعادلة الدالية لـ"دالة إيتا" هي أحد دوافع أويلر لدراسة المتسلسلات المتعلقة بـ 1 − 2 + 3 − 4 + ...، والتي أدت مباشرةً إلى المعادلة الدالية لـ دالة زيتا لريمان. فقد أصبح أويلر مشهورا بإيجاد قيم هذه الدوال عند الأعداد الصحيحة الزوجية (بما في ذلك معضلة بازل)، وحاول إيجاد القيم عند الأعداد الصحيحة الفردية (بما في ذلك ثابتة أبيري) أيضا، وهي مشكلة لم تحل حتى الآن. يمكن التعامل مع دالة إيتا بسهولة بطرق أويلر لأن متسلسلة دركليه قابلة للجمع وفق آبل; بينما دالة زيتا لدركليه يصعب جمعها إذا كانت متباعدة.^[21] على سبيل المثال فإن المقابل للمتسلسلة 1 − 2 + 3 − 4 + ... في دالة زيتا هي المتسلسلة (غير المترددة) 1 + 2 + 3 + 4 + ..., والتي لها تطبيقات هامة في الفيزياء الحديثة لكنها تحتاج طرق أكثر قوة لجمعها.

المراجع

المصادر

موسوعات ذات صلة :

• موسوعة رياضيات
• موسوعة تحليل رياضي