
En thermodynamique, un équilibre thermodynamique correspond à l'état d'un système ne subissant aucune évolution à l'échelle macroscopique. Les grandeurs intensives caractérisant ce système (notamment la pression, la température et les potentiels chimiques) sont alors homogènes dans l'espace et constantes dans le temps. Cet équilibre est stable s'il n'est pas susceptible d'évoluer sur une échelle de temps infinie, ou sous le coup d'une perturbation extérieure ou d'une fluctuation locale interne.
Tout système évolue selon les premier et deuxième principes de la thermodynamique, qui définissent les fonctions d'état énergie interne et entropie. Un équilibre thermodynamique est stable lorsque le système ne peut plus évoluer, car cela impliquerait une diminution de l'entropie contraire au deuxième principe. L'équilibre thermodynamique d'un système isolé (qui n'échange ni travail, ni chaleur, ni matière avec l'extérieur) est caractérisé par un maximum de l'entropie et un minimum de l'énergie interne. L'équilibre d'un système fermé (qui n'échange pas de matière avec l'extérieur) sous contrainte est caractérisé par le minimum d'un potentiel thermodynamique spécifique (qui est également une fonction d'état) correspondant à un maximum de l'entropie globale du système et de son extérieur.
L'entropie et les potentiels thermodynamiques possèdent en conséquence des caractéristiques de concavité ou de convexité qui déterminent le signe de certains coefficients calorimétriques et thermoélastiques, ainsi que certaines propriétés des potentiels chimiques des espèces constituant le système. D'autre part, deux systèmes en équilibre l'un avec l'autre ont atteint simultanément :
- un équilibre mécanique lorsque les deux systèmes ont la même pression ;
- un équilibre thermique lorsque les deux systèmes ont la même température ;
- un équilibre diffusif lorsque chaque espèce chimique a le même potentiel chimique dans les deux systèmes.
Les équilibres de phases et les équilibres chimiques sont des exemples d'équilibres thermodynamiques. Ces principes expliquent également la coalescence des milieux dispersés, ceux-ci tendant à minimiser leur surface.
Définitions et principes généraux
Éléments de définition d'un équilibre thermodynamique
Définition de l'équilibre thermodynamique
Les états d'équilibre sont les objets d'étude de la thermodynamique. Un processus thermodynamique est une transformation d'un système passant d'un état d'équilibre à un autre. Une transformation réversible est effectuée par l'intermédiaire d'équilibres successifs, tandis qu'une transformation irréversible est effectuée via des états hors équilibre. Dans les faits, la définition d'un état d'équilibre est bien souvent circulaire : un système à l'équilibre thermodynamique est un système qui peut être décrit par les lois de la thermodynamique, tandis qu'un échec de la thermodynamique peut être interprété comme une preuve que le système n'est pas à l'équilibre[1].
L'équilibre thermodynamique peut être défini ainsi[1],[2],[3] :
| Équilibre thermodynamique État que tout système isolé atteint après un temps suffisamment long et caractérisé macroscopiquement par un nombre fini de variables d'état. |
Les variables, ou grandeurs, décrivant le système sont extensives : en général on considère le volume , l'énergie interne et les quantités , , etc. des espèces chimiques constituant le système. Les variables décrivant l'équilibre sont intensives : en général on considère la pression , la température et les potentiels chimiques , , etc. des espèces[2],[4]. Ces grandeurs intensives ne sont définies et mesurables qu'à l'équilibre[3].
On ajoute à cette définition la nécessité pour le système d'être homogène et isotrope, c'est-à-dire le fait que les grandeurs intensives sont identiques en tout point du système et ne dépendent pas de la direction selon laquelle le système est observé. Dans les faits, un système peut être à l'équilibre sans être homogène, comme dans le cas d'une colonne de liquide dans laquelle la pression dépend de l'emplacement dans la colonne. Le critère de l'homogénéité permet de simplifier la description thermodynamique du système et de son équilibre. D'autre part, les grandeurs décrivant l'équilibre sont invariantes dans le temps : le système n'évolue plus et ne peut plus évoluer.
Cette définition est issue d'observations courantes qui montrent qu'un système isolé a tendance à évoluer vers un état indépendant de son histoire. Dans la pratique, cette définition pose certaines difficultés, notamment quant à l'établissement d'un système isolé et quant à la durée d'observation nécessaire à l'obtention de l'équilibre.
Systèmes thermodynamiques

 Un ménisque est un effet de surface.
Un ménisque est un effet de surface. Un piston est un système fermé. Son enceinte ne laisse ni entrer ni sortir la matière. Par contre elle est déformable et laisse passer la chaleur.
Un piston est un système fermé. Son enceinte ne laisse ni entrer ni sortir la matière. Par contre elle est déformable et laisse passer la chaleur. Un tube en aluminium (5 mm d'épaisseur) ayant subi une pression extérieure de 700 bar.
Un tube en aluminium (5 mm d'épaisseur) ayant subi une pression extérieure de 700 bar. Le vase de Dewar est un récipient aux parois adiabatiques.
Le vase de Dewar est un récipient aux parois adiabatiques.
Un système thermodynamique, ou système, est une portion de l'Univers délimitée par la pensée du reste de l'Univers, appelé système extérieur ou extérieur[5],[4]. La paroi, aussi appelée enceinte ou enveloppe, qui marque la frontière entre le système et l'extérieur, qui peut être virtuelle, détermine la nature du système selon les échanges qu'elle rend possibles au cours d'une transformation du système. Un système ouvert peut échanger de l'énergie (sous forme de travail et de chaleur) et de la matière avec l'extérieur. Un système fermé peut échanger de l'énergie mais pas de matière. Un système isolé n'échange ni énergie ni matière[4].
Ces divers types de système sont supposés être homogènes, ce qui signifie que les grandeurs intensives (pression, température, potentiels chimiques) qui décrivent un système sont identiques en tout point de ce système. Ceci implique que le système ne baigne pas dans un champ de force extérieur, notamment un champ électromagnétique ou gravitationnel. La gravité induit que la pression n'est pas homogène dans un système réel : dans une colonne de liquide, en raison des lois de l'hydrostatique, la pression est plus forte au fond de la colonne qu'en surface. Par exemple, 10 m de colonne d'eau induisent une différence de pression d'environ 1 bar, et la loi de Henry induit que les concentrations en gaz dissouts dans une telle colonne sont deux fois plus importantes au fond de la colonne qu'en surface. La gravité induit des gradients de pression et de concentration dans une colonne de liquide, qui n'est donc pas homogène. La gravité est un facteur moins influent pour les gaz, qui ont des masses volumiques plus faibles que les liquides. Le volume du système étudié doit par conséquent être suffisamment petit pour pouvoir, expérimentalement, négliger l'influence de champs de forces extérieurs, et notamment de la gravité.
Le volume doit toutefois rester suffisamment important pour éviter les effets de surface. En effet, la matière peut avoir un comportement altéré aux interfaces entre phases : entre un gaz et un liquide, entre les parois d'un récipient et son contenu. Des gradients de concentration peuvent, par exemple, s'établir à ces interfaces, des forces particulières (tension superficielle, etc.) peuvent y agir. Ces phénomènes sont cependant très localisés et négligeables sur des volumes suffisamment importants[6].
Un système fermé n'échange aucune matière avec l'extérieur. Sa paroi est imperméable, aucune matière ne peut la traverser. Par contre, cette paroi peut être déformable, le volume du système peut ainsi évoluer au cours de la transformation par le travail des forces de pression. De même, cette paroi peut laisser passer de la chaleur par conduction ou rayonnement. Un piston est un exemple typique de système fermé. Expérimentalement, l'obtention d'une étanchéité parfaite est le point le plus délicat d'un tel système. De plus, la paroi elle-même ne doit pas subir de dégradation au cours du temps, sous l'effet des déformations ou de la chaleur. Son matériau doit être inerte, il ne doit pas relarguer de composants vers le système, ou absorber des composants du système, ou réagir avec le contenu.
L'absence d'échange de travail avec l'extérieur suppose, outre l'absence d'un champ de force extérieur, que les forces de pression ne peuvent pas déformer le système, et donc que son volume reste constant au cours de la transformation. La paroi du système doit pouvoir résister, le cas échéant, à un vide poussé ou à de fortes pressions, tant à l'intérieur qu'à l'extérieur du système.
L'absence d'échange de chaleur du système avec son environnement est approximativement réalisable à l'aide d'isolants thermiques. Il n'existe pas d'isolant parfait, tout matériau laissant passer, à des degrés divers, de la chaleur par conduction ou rayonnement. La capacité d'un matériau à s'opposer à un flux thermique est appelée résistance thermique ; une transformation effectuée en l'absence d'échange de chaleur avec l'extérieur est dite « adiabatique » et suppose que les parois du système isolé ont une résistance thermique infinie. De tels matériaux n'existent pas, et les déperditions thermiques du système ne peuvent être négligées que sur des temps d'observation réduits[7].
Dans la pratique, un système isolé ne peut donc être réalisé que sur de petits volumes, afin de négliger l'influence de la gravité, mais suffisamment importants pour rendre les effets de surface négligeables. Sa paroi doit être totalement imperméable et inerte vis-à-vis du contenu et de l'extérieur du système, et résister à la différence de pression entre contenu et extérieur. Elle doit de plus empêcher toute déperdition thermique. Dans les faits, un tel système est idéal et n'existe pas, mais on peut obtenir des systèmes s'en approchant sur des temps relativement courts.
Échelle macroscopique, équilibre stationnaire
 À l'échelle microscopique les molécules se déforment en permanence.
À l'échelle microscopique les molécules se déforment en permanence. À l'échelle microscopique les molécules se déplacent en permanence (mouvement brownien).
À l'échelle microscopique les molécules se déplacent en permanence (mouvement brownien). À l'échelle macroscopique aucun mouvement n'est observé.
À l'échelle macroscopique aucun mouvement n'est observé.
En thermodynamique, la matière étudiée est le plus souvent constituée de particules telles que des molécules ou des ions. Ces structures composées d'atomes se déforment en permanence selon leurs degrés de liberté internes. Dans un fluide (liquide, gaz) ces espèces chimiques se déplacent en permanence (mouvement brownien) dans l'espace. Dans un solide les atomes vibrent en permanence autour d'une position moyenne. De même, dans les équilibres chimiques des espèces se transforment en permanence, des réactifs donnant des produits et réciproquement. Dans les équilibres de phases, des particules passent en permanence d'une phase à l'autre au niveau de l'interface entre phases. À l'échelle microscopique, les composants d'un système thermodynamique quelconque ne sont donc jamais figés dans l'espace et le temps. À cette échelle, un système thermodynamique subit en permanence des fluctuations spatiales et temporelles des grandeurs qui le décrivent[1],[2].
À l'échelle macroscopique ces fluctuations et mouvements ne sont pas perceptibles directement, mais sont reflétés par des grandeurs intensives telles que la pression, la température, les potentiels chimiques des espèces chimiques, etc. Lorsque ces grandeurs sont homogènes dans l'espace et constantes dans le temps, l'état du système est décrit comme étant celui d'un équilibre[2],[4]. Cet équilibre est qualifié d'équilibre stationnaire ou d'équilibre dynamique, car à l'échelle microscopique les échanges entre particules et les mouvements de celles-ci ont toujours lieu (au contraire d'un équilibre statique).
Ce sont donc les moyennes des grandeurs intensives mesurées qui décrivent son équilibre : localement, ces grandeurs fluctuent dans le temps et l'espace[2]. Ainsi, la thermodynamique décrit les états macroscopiques de la matière et énonce les lois qui régissent les échanges d'énergie entre de grands ensembles de particules. Elle ne dit rien sur le détail des interactions et mouvements à l'échelle microscopique, dont l'étude relève d'autres domaines de la physique.
Équilibre stable

- Exemple d'équilibre de phase métastable. La perturbation appliquée à cette eau liquide à température négative, en état de surfusion, déclenche son passage à l'état solide.
Certaines transformations extrêmement lentes conduisent à l'observation d'états hors équilibre, dits équilibres instables, qui peuvent paraitre stables sur une échelle de temps relativement longue[1]. Ainsi le diamant est-il une forme instable du carbone : il tend naturellement à se transformer en graphite, qui est la forme stable dans les conditions normales de température et de pression, mais cette réaction n'est observable qu'à des échelles de temps géologiques. De même, des phénomènes de diffusion de la matière peuvent être extrêmement lents et non observables sur des temps courts, l'équilibre apparent observé est également instable.
Certains états observés sont des états hors équilibre qui perdurent dans le temps jusqu'à ce qu'une perturbation déclenche une transformation souvent violente : ces états sont dits équilibres métastables[4]. Par exemple, un mélange d'hydrogène et d'oxygène peut rester stable dans le temps, mais une simple étincelle déclenche une réaction violente qui produit de l'eau. De même, l'eau peut être maintenue liquide en dessous de 0 °C à pression atmosphérique : cet état est appelé état de surfusion, il suffit alors de l'introduction d'une poussière ou d'une fluctuation de température pour que l'eau se solidifie brutalement. Des solutions liquides peuvent contenir un soluté (gaz ou solide) dissout en état de sursaturation, c'est-à-dire à des concentrations plus importantes que celles décrites par la thermodynamique, jusqu'à ce qu'une perturbation déclenche un phénomène brutal de désaturation (respectivement un dégazage et une précipitation) permettant d'établir l'état d'équilibre stable de la solution, l'état de saturation prédit par la thermodynamique.
Un équilibre stable peut donc se définir comme étant un état non susceptible d'évoluer sur une échelle de temps infinie, ni sous le coup d'une perturbation extérieure ou d'une fluctuation locale interne[2],[8],[4].
Principes de la thermodynamique
Premier principe de la thermodynamique
Le premier principe de la thermodynamique est un principe de conservation de l'énergie interne, notée .
| Premier principe de la thermodynamique Au cours d'une transformation quelconque, la variation de l'énergie interne d'un système fermé |
En conséquence, l'énergie interne d'un système isolé ne varie pas au cours de la transformation, soit :
Si un système fermé, d'énergie interne , et son extérieur, d'énergie interne , forment ensemble un système isolé, alors l'énergie globale du système isolé est invariante : . Ainsi, l'une des deux énergies et peut varier du moment que l'autre énergie compense cette variation par une variation opposée.
Deuxième principe de la thermodynamique
Le deuxième principe de la thermodynamique est un principe d'évolution de la transformation ayant lieu dans le système. Ce principe introduit la notion d'entropie, notée .
Pour un système fermé échangeant de la chaleur avec un autre système, l'entropie est définie par l'inégalité de Clausius :
| Entropie, inégalité de Clausius : |
avec la température absolue. La transformation est[9] :
- réversible si ;
- irréversible si .
Dans un système isolé, n'échangeant pas de chaleur avec l'extérieur, soit , un processus réversible se traduit donc par et un processus irréversible par . Le deuxième principe de la thermodynamique énonce que :
| Deuxième principe de la thermodynamique Au cours d'une transformation quelconque, l'entropie d'un système isolé ne peut qu'augmenter : |
Soit un système fermé ou isolé, siège d'une transformation quelconque impliquant un échange de chaleur à température . On note[10],[11],[12] :
avec :
- la variation d'entropie du système due à la transformation ;
- la variation d'entropie due exclusivement à l'échange de chaleur avec l'extérieur ; est l'entropie d'échange ;
- la génération d'entropie (aussi appelée création ou production d'entropie), liée à l'irréversibilité de la transformation ; est l'entropie d'irréversibilité.
Le terme peut être positif (le système gagne de la chaleur), nul (processus adiabatique) ou négatif (le système perd de la chaleur). Le terme ne peut être que positif (dans une transformation irréversible) ou nul (dans une transformation réversible). On note également :
Le terme est appelé travail non compensé ou chaleur non compensée. Il ne peut être que positif ou nul[11],[12].
Si est négatif, l'entropie d'un système fermé peut diminuer, soit . On note l'entropie de l'extérieur de ce système. En vertu du deuxième principe, le système et son extérieur formant un système isolé, l'entropie globale ne peut qu'augmenter, soit . L'entropie du système peut donc diminuer si la variation d'entropie de l'extérieur compense cette diminution de telle sorte que . Si l'entropie du système fermé diminue, l'entropie de l'extérieur ne peut qu'augmenter de façon que l'entropie globale du système isolé augmente. Inversement, l'entropie de l'extérieur peut également diminuer si l'entropie du système fermé augmente et si l'entropie globale du système isolé augmente.
Potentiels thermodynamiques
Considérons un système fermé, appelé « système » par la suite, subissant une transformation quelconque. Ce système et son extérieur forment ensemble un système isolé qui possède son propre extérieur. Nous posons :
- la pression, en considérant que le système et son extérieur sont constamment à la même pression, celle-ci pouvant évoluer ;
- la température, en considérant que le système et son extérieur sont constamment à la même température, celle-ci pouvant évoluer ;
- le volume du système ;
- le volume de l'extérieur du système.
Par définition, le système isolé n'échange pas de travail avec son propre extérieur. Il n'y a donc aucune force de pression pour déformer son volume : le travail . Le volume du système étudié peut donc évoluer au cours de la transformation en respectant la contrainte :
Pour le système, nous considérons :
- qu'il produit un travail des forces de pression égal à ;
- qu'il est le siège d'une transformation potentiellement irréversible, soit ; il peut s'agir, entre autres :
- du travail d'une force utile non récupéré, qui est alors dégradé en chaleur ;
- de travaux de forces non récupérables, telles que les frottements ou la viscosité, qui sont également dégradés en chaleur ;
- d'une réaction chimique ou d'un phénomène diffusif.
On pose : . Le terme représente la variation d'énergie due à la transformation du système fermé. Ce terme doit être négatif selon le deuxième principe, il s'agit de l'opposé de la chaleur non compensée : . La variation de l'énergie interne du système vaut en conséquence :
Pour l'extérieur, nous considérons :
- qu'il produit un travail des forces de pression égal à ;
- qu'il reçoit la chaleur émise par le système et que la transformation est réversible : .
La variation de l'énergie interne de l'extérieur vaut en conséquence :
En application du premier principe, puisque le système et l'extérieur forment un système isolé, l'énergie globale est conservée :
En application du deuxième principe, puisque le système et l'extérieur forment un système isolé, l'entropie globale ne peut que croître :
À partir des relations (1), (2) et (3), on appelle potentiel thermodynamique une fonction d'état, notée de façon générique , telle que[13] :
| Potentiel thermodynamique |
On vérifie l'inégalité de Clausius : .
Les divers potentiels thermodynamiques sont créés en fixant certaines conditions de la transformation[13] :
- à volume et entropie constants : ;
- énergie libre, ou fonction de Helmholtz, :
- à volume et température constants : ;
- à pression et entropie constantes : ;
- enthalpie libre, ou fonction de Gibbs, :
- à pression et température constantes : .
Au cours de la transformation, l'une des deux entropies et peut décroître, du moment que l'entropie globale du système isolé croît. Les potentiels thermodynamiques ne peuvent que décroître.
Convexité des fonctions thermodynamiques
Concavité de l'entropie

Les variables de l'entropie sont toutes extensives : volume , énergie interne , quantité de matière , etc. On les note de façon générique À l'équilibre, l'entropie est elle-même une fonction extensive : si l'on met en contact deux systèmes et à l'équilibre, alors l'entropie globale du système résultant vaut . À contrario, si les deux systèmes fusionnés ne sont pas à l'équilibre, il y a, en vertu du deuxième principe, création d'entropie au cours du processus de fusion, et, lorsque le nouveau système a atteint l'équilibre, on a[14],[15] : .
Considérons deux systèmes thermodynamiques quelconques isolés, notés et , par exemple deux phases différentes, deux réservoirs de réactifs chimiques, deux solides à températures différentes, etc. Chacun de ces deux systèmes est à l'équilibre thermodynamique indépendamment de l'autre. Ils ont respectivement pour entropie[14],[15] :
On prélève une fraction quelconque (comprise entre 0 et 1) du système et une fraction du système . Les variables de l'entropie étant extensives, ces fractions de systèmes et sont définies respectivement par des fractions des variables initiales :
L'entropie étant elle-même extensive à l'équilibre, les entropies de ces deux fractions de systèmes sont des fractions des entropies des systèmes et initiaux et valent respectivement[14],[15] :
Ces deux fractions sont mises en contact de façon à former un nouveau système isolé . Puisque les variables de l'entropie sont toutes extensives, elles s'additionnent. En particulier, en vertu du premier principe, le nouveau système étant isolé, son énergie interne ne peut pas évoluer et ne peut qu'être égale à . Le nouveau système est par conséquent défini par les variables :
et son entropie est une fonction telle que[14],[15] :
Si les deux fractions sont déjà à l'équilibre thermodynamique entre elles au moment de leur mise en contact, alors le nouveau système n'évolue pas et a pour entropie . Si les deux fractions ne sont pas immédiatement à l'équilibre entre elles, alors le nouveau système est le siège d'une transformation (par exemple un transfert de chaleur, une diffusion de matière d'un sous-système à l'autre, une réaction chimique…). En vertu du deuxième principe, l'entropie du nouveau système ne peut qu'augmenter au cours de cette transformation et, lorsque celui-ci a atteint l'équilibre, ne peut qu'être supérieure à la somme des entropies des deux fractions. À l'équilibre de ce nouveau système on a par conséquent[14],[15] :
L'entropie est donc une fonction concave[16] par rapport à ses variables naturelles[17]. En termes mathématiques, la matrice hessienne de l'entropie est définie négative[16], d'où[14],[15],[18],[19] :
| L'entropie est une fonction concave : |
Convexité de l'énergie interne

On considère un système fermé siège d'une transformation quelconque, que l'on traduit par le terme dans la différentielle du premier ordre de [20] :
Les variables sont les mêmes pour l'énergie interne et l'entropie. Les variables de l'énergie interne (volume, entropie, quantité de matière, etc.) sont par conséquent toutes extensives. On a la différentielle du deuxième ordre de l'énergie interne :
Pour l'entropie on a, par réagencement de :
Par substitution de on obtient :
Par conséquent :
Puisque la température thermodynamique ne peut être que positive, alors et sont de signes opposés. L'entropie étant une fonction concave, l'énergie interne est une fonction convexe[16] par rapport à ses variables naturelles. En termes mathématiques, la matrice hessienne de l'énergie interne est définie positive[16], d'où[21] :
| L'énergie interne est une fonction convexe : |
Convexité des autres potentiels thermodynamiques
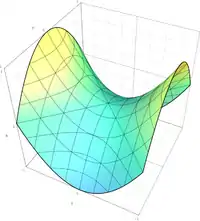
Les potentiels thermodynamiques sont des transformées de Legendre de l'énergie interne . Cette transformation remplace une variable extensive de par une variable intensive du potentiel thermodynamique résultant, tout en inversant la convexité de la fonction par rapport à cette variable. En conséquence, les potentiels thermodynamiques sont concaves par rapport à leur(s) variable(s) intensive(s) et convexes par rapport à leurs variables extensives (voir la section Notations et outils mathématiques)[22],[23] :
- l'énergie interne est convexe par rapport à toutes ses variables, qui sont toutes extensives : volume , entropie , quantité de matière , etc. ;
- l'énergie libre est concave par rapport à la température et convexe par rapport au volume , à la quantité de matière , etc. ;
- l'enthalpie est concave par rapport à la pression et convexe par rapport à l'entropie , la quantité de matière , etc. ;
- l'enthalpie libre est concave par rapport à la pression et la température , et convexe par rapport à la quantité de matière , etc.
Les potentiels thermodynamiques , et sont donc des fonctions convexes-concaves.
Conditions d'établissement d'un équilibre stable
Entropie et énergie interne
Soit un système fermé n'échangeant avec l'extérieur que le travail des forces de pression et de la chaleur . Le terme générique représente le travail de forces autres que les forces de pression, ou une réaction chimique, etc., ce travail non récupéré étant dégradé en chaleur. Les variables sont toutes extensives (par exemple les quantités des diverses espèces présentes). L'énergie interne du système varie donc selon :
et son entropie selon :
Le système évolue selon les premier et deuxième principes de la thermodynamique :
L'entropie est concave :
L'énergie interne est convexe :
Équilibre d'un système isolé
Évolution d'un système isolé
Un système isolé n'échange ni travail, soit , ni chaleur, soit , ni matière avec l'extérieur. En l'absence d'un travail de forces de pression échangé avec l'extérieur, soit , le système évolue à volume constant, soit . En l'absence de tout autre échange avec l'extérieur, l'énergie interne et l'entropie de celui-ci ne varient pas. Selon le premier principe de la thermodynamique, le système isolé évolue à énergie interne constante. On obtient :
Le système isolé évolue selon :
Les différentielles du deuxième ordre donnent :
À l'équilibre l'entropie du système n'évolue plus, soit . Ainsi, à l'équilibre :
On étudie la variation d'un paramètre quelconque du système à partir de cet équilibre.
Principe de l'entropie maximale
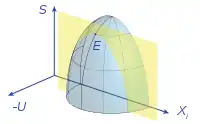
À partir du point d'équilibre stable E, à énergie interne constante (plan jaune), toute variation d'un paramètre de l'équilibre ne peut induire qu'une diminution de l'entropie : l'entropie a atteint un maximum au point E.
À l'équilibre on a et , qui se traduisent, à volume et énergie interne constants, pour toute variation d'un paramètre quelconque, par :
À l'équilibre l'entropie atteint donc un maximum (voir la figure 1). Toute variation à partir de cet équilibre, à volume et énergie interne constants, d'un paramètre quelconque ne peut que faire diminuer l'entropie, ce qu'interdit le deuxième principe de la thermodynamique. Le système ne peut plus évoluer, l'équilibre est stable, d'où le principe de l'entropie maximale[24],[25],[26] :
| Principe de l'entropie maximale L'état d'équilibre stable d'un système isolé est caractérisé par une entropie maximale : |
Principe de l'énergie interne minimale

À partir du point d'équilibre stable E, à entropie constante (plan jaune), toute variation d'un paramètre de l'équilibre ne peut induire qu'une augmentation de l'énergie interne : l'énergie interne a atteint un minimum au point E.
À l'équilibre on a et , qui se traduisent, à volume et entropie constants, pour toute variation d'un paramètre quelconque, par :
À l'équilibre, l'énergie interne correspond donc à un minimum (voir la figure 2). Toute variation à partir de cet équilibre, à volume et entropie constants, d'un paramètre quelconque ne peut que faire augmenter l'énergie interne, ce qu'interdit le premier principe de la thermodynamique. Le système ne peut plus évoluer, l'équilibre est stable, d'où le principe de l'énergie minimale[27],[28] :
| Principe de l'énergie interne minimale L'état d'équilibre stable d'un système isolé est caractérisé par une énergie interne minimale : |
Équilibre d'un système fermé sous contrainte
Évolution d'un système fermé
Un système fermé échange du travail et de la chaleur avec l'extérieur, mais pas de matière[4]. On considère qu'il forme avec l'extérieur un système isolé, aussi évolue-t-il selon :
soit :
À l'équilibre on a :
L'extérieur constitue un réservoir qui permet de maintenir constantes certaines caractéristiques du système fermé étudié. Ce réservoir est supposé suffisamment grand, en regard du système étudié, pour que les échanges avec le système ne modifient pas de façon significative ses propres caractéristiques, qui sont donc considérées comme constantes au cours de la transformation. Par exemple, un réacteur (système étudié) en équilibre de pression et de température avec l'atmosphère (extérieur) reste constamment à pression et température atmosphériques, qui ne varient pas. L'atmosphère reçoit le travail des forces de pression et la chaleur du réacteur, mais cet apport d'énergie est bien insuffisant pour modifier sa pression et sa température. L'extérieur impose donc des contraintes au système fermé étudié.
Au cours de cette transformation, l'une des deux entropies et peut décroître, du moment que l'entropie globale du système isolé croît.
À volume et entropie constants
Pour un système évoluant à volume et entropie du système constants, soit et , on a :
L'entropie du système est constante, mais l'entropie de l'extérieur augmente. Le système évolue spontanément dans le sens d'une diminution de l'énergie interne , mais l'énergie interne globale est constante. Dans ces conditions, l'énergie interne est convexe. Lorsque l'équilibre est atteint, ne varie plus, alors :
Par conséquent[28] :
| Dans une transformation à volume et entropie constants, l'énergie interne d'un système fermé diminue. L'équilibre stable est caractérisé par un minimum de . |
À volume et température constants
On introduit l'énergie libre du système :
Pour un système évoluant à volume et température constants, soit et , on a :
L'entropie globale augmente. Le système évolue spontanément dans le sens d'une diminution de l'énergie libre . Dans ces conditions, l'énergie libre est convexe. Lorsque l'équilibre est atteint, ne varie plus, alors :
Par conséquent[29] :
| Dans une transformation à volume et température constants, l'énergie libre d'un système fermé diminue. L'équilibre stable est caractérisé par un minimum de . |
À pression et entropie constantes
On introduit l'enthalpie du système :
Pour un système évoluant à pression et entropie constantes, soit et , on a :
L'entropie du système est constante, mais l'entropie de l'extérieur augmente. Le système évolue spontanément dans le sens d'une diminution de l'enthalpie . Dans ces conditions, l'enthalpie est convexe. Lorsque l'équilibre est atteint, ne varie plus, alors :
Par conséquent[30] :
| Dans une transformation à pression et entropie constantes, l'enthalpie d'un système fermé diminue. L'équilibre stable est caractérisé par un minimum de . |
À pression et température constantes
On introduit l'enthalpie libre du système :
Pour un système évoluant à pression et température constantes, soit et , on a :
L'entropie globale augmente. Le système évolue spontanément dans le sens d'une diminution de l'enthalpie libre . Dans ces conditions, l'enthalpie libre est convexe. Lorsque l'équilibre est atteint, ne varie plus, alors :
Par conséquent[31] :
| Dans une transformation à pression et température constantes, l'enthalpie libre d'un système fermé diminue. L'équilibre stable est caractérisé par un minimum de . |
Implications
Conditions de stabilité
Expression des conditions de stabilité
La concavité de l'entropie et la convexité de l'énergie interne induisent que leurs dérivées secondes, ainsi que celles des autres potentiels thermodynamiques, doivent répondre à certaines contraintes, notamment quant à leur signe (voir la section Notations et outils mathématiques). L'équilibre d'un système dans lequel l'une de ces dérivées secondes ne vérifie pas ces contraintes ne peut être stable, car il enfreint le deuxième principe de la thermodynamique. Ainsi les critères de convexité de l'entropie et des potentiels thermodynamiques induisent-ils les conditions de stabilité d'un système. Les conditions données ci-dessous sont toutefois nécessaires, mais pas suffisantes.
Dans les expressions ci-dessous, le théorème de Schwarz permet d'écrire, pour l'entropie comme pour tout potentiel thermodynamique, et pour deux variables quelconques : . Ainsi, les conditions données pour sont également valables pour .
Les conditions de stabilité relatives aux dérivées partielles secondes de l'entropie sont :
L'entropie est une fonction concave par rapport à toutes ses variables, qui sont toutes extensives[18].
Les conditions de stabilité relatives aux dérivées partielles secondes des potentiels thermodynamiques sont[23] :
Conclusions générales
En résumé, pour tout potentiel thermodynamique , étant les variables naturelles de , dont et :
- si est intensive (pression, température) :
- Les potentiels thermodynamiques sont concaves par rapport à leurs variables naturelles intensives[22],[23] ;
- si est extensive (volume, entropie, quantité de matière) :
- Les potentiels thermodynamiques sont convexes par rapport à leurs variables naturelles extensives[22],[23] ;
- si et sont simultanément intensives ou extensives :
- , soit .
- Cette contrainte donne une indication sur la valeur absolue de la dérivée croisée, mais pas sur son signe ;
- si est intensive et extensive, il n'y a pas de condition sur la dérivée croisée .
Soit la variable conjuguée[32] de :
On note la variation de induite par une modification de à constantes :
On a donc, pour toutes variables constantes :
Les conditions de stabilité donnent si est intensive, et si est extensive. Par conséquent tout système évolue, à constantes, selon :
En conclusion :
| La modification d'une variable intensive induit une modification opposée de sa variable conjuguée[32] extensive . |
La modification d'une variable extensive induit une modification dans le même sens de sa variable conjuguée intensive . |
Exemple 1 - Évolutions réciproques de la pression et du volume.
- Selon (edeV) et l'enthalpie libre , la variable conjuguée de la pression est le volume : . La pression étant une variable intensive, une augmentation de pression, à température et composition constantes, induit une diminution du volume, variable extensive. Il s'agit de la conséquence de (csG1).
- Selon (edeP) et l'énergie libre , la variable conjuguée du volume est l'opposé de la pression : . Le volume étant une variable extensive, une augmentation du volume, à température et composition constantes, induit une augmentation de , variable intensive, soit une diminution de la pression. Il s'agit de la conséquence de (csF1).
Soit une variable de différente de . On note la variation de induite par une modification de à constantes :
On a donc, pour toutes variables constantes :
et étant différentes, le signe de n'est pas imposé par les conditions de stabilité, que ces deux variables soient simultanément ou non extensives ou intensives. Le signe de n'est donc pas défini, il peut être positif ou négatif. En conclusion :
| Il est impossible de prévoir le sens de variation de en fonction d'une modification d'une autre variable du potentiel thermodynamique . |
Exemple 2 - Évolution du volume en fonction de la quantité d'un produit.
- Le signe du volume molaire partiel d'un corps dans un mélange n'est pas imposé par les conditions de stabilité. Avec (edeV), soit , on a . Il n'y a pas de contrainte de signe sur cette dérivée croisée : on ne peut prévoir la variation de en fonction de la quantité de l'espèce . Le volume molaire partiel d'un corps peut être aussi bien positif (le volume d'un mélange augmente lorsque l'on ajoute ) que négatif (le volume d'un mélange diminue lorsque l'on ajoute ), ce qui est toutefois assez rare[33]. Par exemple, lorsque l'on dissout 0,1 mole de sulfate de magnésium MgSO4 dans un litre d'eau, le volume de la solution obtenue est inférieur à un litre. Le volume se contracte par addition de MgSO4, son volume molaire partiel est donc négatif[34].
- Par ailleurs, le théorème de Schwarz donne avec la définition (mu) . Il est donc également impossible de prévoir l'évolution d'un potentiel chimique en fonction de la pression .
Coefficients calorimétriques et thermoélastiques

En raison de sa capacité thermique positive, une bouillote accumule de la chaleur lorsque sa température augmente.
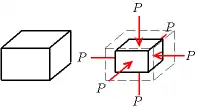
En raison de sa compressibilité positive, le volume d'un corps diminue lorsque la pression extérieure augmente.
Parmi les coefficients calorimétriques et thermoélastiques sont définis :
| (csCV) : |
- le coefficient de compressibilité isentropique ; étant donné les équations d'état (edeV) et (edeP) on a :
| (csChiS) : |
- un coefficient sans nom ; étant donné l'équation d'état (edeP) on a :
- La condition de stabilité (csU4) donne :
| (csLambda) : |
| (csCP) : |
- le coefficient de compressibilité isotherme ; étant donné les équations d'état (edeV) et (edeP) on a :
| (csChiT) : |
- le coefficient de dilatation isobare ; étant donné l'équation d'état (edeV) on a :
- La condition de stabilité (csG4) donne :
| (csAlpha) : |
Les capacités thermiques et positives correspondent aux observations communes : un corps absorbe de la chaleur lorsque sa température augmente et en restitue lorsqu'elle diminue. De même, le volume d'un corps diminue sous l'effet de la pression : les coefficients de compressibilité et sont positifs. La thermodynamique n'interdit pas que ces coefficients soient négatifs, mais un corps présentant de telles propriétés serait instable considéré seul car il diminuerait l'entropie, en contradiction avec le deuxième principe de la thermodynamique : une telle situation est donc difficilement observable. Cependant des coefficients négatifs peuvent être observés dans un contexte impliquant des phénomènes compensant cette instabilité. En physique stellaire la stabilité des étoiles est expliquée par une capacité thermique négative due à l'attraction gravitationnelle entre ses constituants. Une étoile génère par fusion nucléaire plus d'énergie qu'elle ne peut en rayonner, ce qui, avec une capacité thermique positive, induirait une telle accumulation de chaleur, et donc une telle augmentation de température, que l'étoile serait instable et mourrait rapidement. La capacité thermique négative permet d'accumuler la chaleur tout en maintenant une température stable[37]. D'autre part, des coefficients de compressibilité négatifs ont été observés sur des mousses métalliques et des cristaux composés d'eau et de méthanol, ces phénomènes étant expliqués par l'architecture des cristaux à l'échelle moléculaire[38],[39],[40].
Le volume d'un corps augmente généralement sous l'effet d'une augmentation de la température, aussi le coefficient de dilatation isobare est-il le plus souvent positif. Néanmoins, la relation (csAlpha) n'impose pas le signe de ce coefficient, qui peut donc être négatif pour un corps stable[41]. L'eau liquide en est un exemple entre 0 °C et 4 °C sous 1 atm : une augmentation de la température provoque une contraction du volume, d'où un maximum de densité à 4 °C, constituant une anomalie dilatométrique[42]. Si l'on considère la variation du volume en fonction de la pression, de la température et de la composition, on a :
Les conditions de stabilité donnent mais ne donnent pas le signe de et , qui peuvent donc être positifs ou, plus rarement, négatifs.
Potentiel chimique
Les conditions de stabilité (csU3), (csF3), (csH3), (csG3), avec les définitions (mu), donnent respectivement[43] :
Le potentiel chimique d'une espèce chimique quelconque augmente lorsque l'on augmente la quantité de cette espèce, les quantités des autres constituants restant constantes (en l'absence de réaction chimique), et ce quelles que soient les autres conditions opératoires également maintenues constantes.
Les conditions de stabilité (csU5), (csU6), (csF4) et (csH4), avec les définitions (mu), les équations d'état (edeP) et (edeT), et le théorème de Schwarz, donnent respectivement, pour toute espèce chimique :
Ces conditions montrent, entre autres, qu'il est impossible de prévoir la variation de la pression ou de la température d'un système en fonction de la variation (ajout ou extraction en l'absence de réaction) de la quantité de l'un de ses constituants . Autrement dit, lors de l'ajout d'un constituant à un système, toutes choses étant égales par ailleurs, la pression et la température peuvent indifféremment augmenter ou diminuer dans un système stable.
Les conditions de stabilité (csU7), (csF5), (csH5) et (csG5), avec les définitions (mu) et le théorème de Schwarz, donnent respectivement, pour deux espèces chimiques et quelconques :
Ces conditions montrent qu'il est impossible de prévoir l'évolution du potentiel chimique d'un constituant dans un mélange en fonction de la variation de la quantité d'un autre constituant , toutes choses étant égales par ailleurs.
Équilibre d'un système hétérogène
Conditions générales d'équilibre
On considère un système isolé hétérogène : il peut être subdivisé en plusieurs sous-systèmes ayant chacun sa propre pression, sa propre température et ses propres potentiels chimiques. Il peut s'agir par exemple de phases différentes, mais il peut également s'agir de deux zones distinctes au sein d'une même phase (par exemple une barre de métal ayant des températures différentes aux deux extrémités). Soit deux sous-sytèmes notés et . Le système global isolé subit une transformation afin d'atteindre l'équilibre. On écrit pour chacun des deux sous-systèmes la variation d'énergie interne[44] :
avec la grandeur relative au sous-système . Soit, pour le système isolé global, les fonctions globales énergie interne globale , entropie globale , volume global et quantité globale de chacun des corps . On a les relations sur le système global isolé, en l'absence de réaction chimique[44] :
- (premier principe de la thermodynamique) ;
- (deuxième principe de la thermodynamique) ;
- (absence de travail des forces de pression) ;
- pour tout (conservation de la matière).
Les grandeurs globales du système global isolé (de l'ensemble constitué par les deux sous-systèmes) sont constantes (hormis l'entropie), mais les grandeurs propres à chacun des deux sous-systèmes, elles, peuvent varier au cours de la transformation, leurs variations étant opposées. Par exemple, le volume global du système isolé, , est constant, mais les volumes des sous-systèmes et peuvent varier et .
On obtient les relations globales d'évolution du système isolé :
L'équilibre est atteint lorsque l'entropie globale du système atteint un maximum. Les variations d'entropie des deux sous-systèmes sont alors liées par : . On peut donc écrire pour le système global à l'équilibre[45],[44] :
Quand les deux sous-systèmes sont à l'équilibre, cela ne signifie pas qu'il n'y a pas d'échanges entre eux. Les deux sous-systèmes continuent à échanger de la matière et de l'énergie, mais globalement les échanges se font dans les deux sens et se compensent : l'état d'équilibre obtenu est qualifié de dynamique ou stationnaire (voir la section Échelle macroscopique, équilibre stationnaire). Les variations , et pour tout sont donc non nulles à l'équilibre. La relation précédente implique par conséquent l'homogénéité des potentiels mécanique (pression), thermique (température) et chimiques (potentiels chimiques) entre les deux sous-systèmes à l'équilibre[44] :
- ;
- ;
- pour tout .
Une autre façon d'obtenir ce résultat est de considérer que lorsque l'équilibre est atteint, c'est-à-dire lorsque l'entropie du système isolé est maximale (voir la figure 1), alors l'énergie globale du système isolé (constante) correspond à un minimum par rapport aux diverses variables du système (voir la figure 2), ce qui implique que :
- ;
- ;
- pour tout .
Les conditions d'équilibre sont donc données par[44] :
| Équilibre mécanique | homogénéité de la pression |
|---|---|
| Équilibre thermique | homogénéité de la température |
| Équilibre diffusif | homogénéité des potentiels chimiques pour tout corps : |
Si le système contient un troisième sous-système , celui-ci doit être à l'équilibre avec les sous-systèmes et : il sera par conséquent à l'équilibre aux mêmes pression, température et potentiels chimiques. Ces conditions sont donc généralisables à plus de deux sous-systèmes en équilibre (gaz-liquide-liquide ou gaz-liquide-solide par exemple, ou multiples phases liquides[46] ou solides).
Note sur l'homogénéité des potentiels chimiques
- L'homogénéité des potentiels chimiques signifie que pour le corps 1 , pour le corps 2 , … , pour le corps , mais pas que ces potentiels sont égaux entre corps différents : .
En conséquence, si deux sous-systèmes d'un système isolé ont des températures différentes, celles-ci tendent à s'homogénéiser par transfert thermique (transfert de chaleur). De même, si à un instant donné une espèce chimique quelconque a des potentiels chimiques différents en deux points de ce système, alors par diffusion les potentiels chimiques tendent à s'homogénéiser. Par exemple, au sein d'une même phase, des concentrations ou des fractions molaires ou massiques tendent à s'égaliser en tout point. Dans la plupart des cas, l'équilibre mécanique s'établit très rapidement, suivi par l'équilibre thermique. L'équilibre diffusif, ou chimique, peut être beaucoup plus lent à atteindre[44].
Le transfert thermique
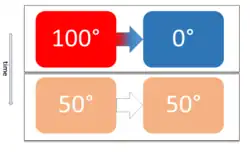
Deux corps à des températures différentes sont mis en contact. Ils échangent de la chaleur. La température la plus haute baisse, la plus basse augmente. À l'équilibre thermique les deux températures sont égales, l'échange de chaleur cesse.
Lorsqu'un milieu est hétérogène en température, celle-ci n'est pas identique en tout point du milieu. Spontanément, de la chaleur migre des zones de température élevée vers les zones de température plus basse : l'entropie du système est ainsi maximisée, conformément au deuxième principe de la thermodynamique. Ce phénomène est appelé transfert thermique.
On considère un système isolé divisé en deux compartiments, et , séparés par une paroi fixe diathermane[47],[48]. Le seul échange possible entre ces deux compartiments est donc un transfert thermique, soit un échange de chaleur. Le volume du système global ne varie pas en l'absence de travail des forces de pression avec l'extérieur, et les volumes des compartiments sont également invariants par la fixité de la paroi.
Il n'est fait aucune hypothèse quant aux pressions, compositions et phases des compartiments, qui peuvent donc être différentes d'un compartiment à l'autre. Les pressions peuvent évoluer au cours de la transformation. On suppose que les compositions sont invariantes en l'absence de réaction chimique.
La variation d'énergie de chacun des compartiments vaut, en considérant que les transformations n'impliquent que de la chaleur :
Le système étant isolé, on a les relations :
- (premier principe, énergie globale ) ;
- (deuxième principe, entropie globale ).
Les températures absolues et étant positives, la première relation induit que les entropies et des deux compartiments varient en sens inverses : . En conséquence et varient également en sens inverses : si l'une augmente, l'autre diminue. On obtient finalement :
On suppose que la température du compartiment est plus importante que celle du compartiment , soit . La température absolue étant positive et, selon le deuxième principe de la thermodynamique, l'entropie du système ne pouvant qu'augmenter, soit , alors , d'où , et : la chaleur diminue dans le compartiment et augmente dans le compartiment . En conséquence, la chaleur migre du compartiment , dans lequel la température est la plus élevée, vers le compartiment , de moindre température. Cette relation ne permet pas de déterminer les variations des températures et des deux compartiments.
Les deux compartiments évoluant à volume constant et en l'absence de réaction chimique, on a par définition des capacités thermiques isochores et respectives des deux compartiments :
La condition de stabilité (csCV) donne :
Puisque et , on a et . Dans le compartiment , où elle est la plus élevée, la température diminue. Elle augmente dans le compartiment , où elle est la plus basse. Au cours du transfert thermique, l'écart tend donc à diminuer.
Le transfert thermique cesse lorsque les températures des deux compartiments sont égales, soit , d'où . L'entropie ne varie plus et le système atteint un équilibre. Si l'entropie continuait à diminuer, alors continuerait à diminuer et à augmenter, d'où et . De même, si l'entropie augmentait à partir de cet équilibre, soit , alors augmenterait et diminuerait, d'où et . L'entropie globale , à partir de l'équilibre atteint, ne peut que diminuer, ce qui est contraire au deuxième principe de la thermodynamique : l'entropie a donc atteint un maximum et ne peut plus évoluer, cet équilibre est stable (voir la figure 1 avec ).
Si l'on considère une transformation à entropie constante (), alors :
Un raisonnement similaire à celui tenu à énergie constante montre que toute évolution de dans ces conditions à partir de l'équilibre (, d'où ) ne peut induire qu'une augmentation de l'énergie interne globale , soit , ce qui est contraire au premier principe de la thermodynamique : l'énergie interne a donc atteint un minimum, cet équilibre est stable (voir la figure 2 avec ).
Pour résumer, si deux compartiments sont mis en contact de telle sorte qu'ils ne puissent échanger que de la chaleur, la chaleur passe du compartiment de plus haute température à celui de moindre température. La température la plus haute diminue et la plus basse augmente. L'équilibre thermique est atteint lorsque les deux températures s'égalisent. L'entropie du système a alors atteint un maximum et son énergie interne un minimum.
Le principe zéro de la thermodynamique

Une paroi adiabatique ne laisse pas passer la chaleur, contrairement à une paroi diathermane. Si A et C sont initialement en équilibre thermique, ainsi que B et C, alors, après inversion des parois, A et B sont immédiatement en équilibre thermique, sans besoin d'échanger de la chaleur.
Le principe zéro de la thermodynamique énonce que[49],[50] :
| Principe zéro de la thermodynamique Si deux systèmes A et B sont en équilibre thermique stable avec un troisième C, ils sont eux-mêmes en équilibre thermique stable. |
Pour l'état initial, on a les deux équilibres, entre A et B d'une part, et B et C d'autre part :
On a alors . Lorsque l'on met en contact A et B, les deux systèmes sont immédiatement à l'équilibre, puisque :
Comme vu dans la section Le transfert thermique, à partir de cet équilibre l'entropie du système A+B ne peut que diminuer, ce qu'interdit le deuxième principe de la thermodynamique. Le système A+B est donc d'emblée à l'équilibre thermique stable, sans qu'un transfert thermique soit nécessaire pour l'établir. Ainsi le principe zéro de la thermodynamique se déduit-il des premier et deuxième principes[50].
Ce principe permet de définir la notion de température comme une grandeur caractéristique de l'état d'équilibre thermodynamique. Tous les corps à la même température sont en équilibre thermique. En conséquence, le thermomètre est un instrument qui permet de vérifier cet équilibre[51].
La diffusion de la matière
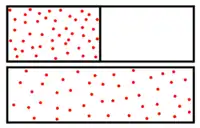
Dans un système isolé, une espèce chimique (ici en rouge) migre d'un compartiment où son potentiel chimique est élevé vers un compartiment où son potentiel est plus bas (figure supérieure). La migration cesse lorsque le potentiel chimique de l'espèce est homogène dans le système (figure inférieure).
Lorsqu'un milieu est hétérogène en composition, le potentiel chimique d'au moins une espèce chimique n'est pas identique en tout point du milieu. Spontanément, chaque espèce migre vers les lieux où son potentiel chimique est le plus bas : l'entropie du système est ainsi maximisée, conformément au deuxième principe de la thermodynamique. Ce phénomène est appelé diffusion de la matière, ou migration.
On considère un système isolé divisé en deux compartiments et séparés par une paroi. Cette paroi n'est perméable qu'à la seule espèce chimique . Elle peut être mobile : le volume de chacun des deux compartiments peut varier, mais le volume global du système, en l'absence de travail des forces de pression avec l'extérieur, est constant. Ces deux compartiments sont supposés être en permanence à l'équilibre mécanique (même pression ) et à l'équilibre thermique (même température ). On suppose enfin que la pression et la température sont constantes et que le système n'est le siège d'aucune réaction chimique.
Il n'est fait aucune hypothèse quant aux autres espèces chimiques du système, qui peuvent donc être différentes d'un compartiment à l'autre, ou à des concentrations différentes de part et d'autre de la paroi. Les deux compartiments peuvent être dans des phases différentes.
La variation d'énergie de chacun des compartiments vaut, en considérant que seule la quantité de l'espèce varie dans les compartiments :
Le système étant isolé, en l'absence de réaction, on a les relations :
- (premier principe, énergie globale ) ;
- (deuxième principe, entropie globale ) ;
- (absence de travail des forces de pression) ;
- (conservation de la matière).
Les quantités et dans les deux compartiments varient donc en sens inverses : , si l'une augmente, l'autre diminue. On obtient finalement[52] :
On suppose que le potentiel chimique de l'espèce est plus important dans le compartiment que dans le compartiment , soit . La température absolue étant toujours positive et, selon le deuxième principe de la thermodynamique, l'entropie du système ne pouvant qu'augmenter, soit , alors , d'où : la quantité de diminue dans le compartiment et augmente dans le compartiment . En conséquence, le corps migre du compartiment , dans lequel son potentiel est le plus important, vers le compartiment , de moindre potentiel. Cette relation ne permet pas de déterminer les variations des potentiels chimiques et dans les deux compartiments.
Les deux compartiments évoluant à pression et température constantes, et en l'absence de réaction chimique, on a les variations des potentiels chimiques dans les deux compartiments :
La condition de stabilité (csMu4) donne :
Puisque et , on a et . Dans le compartiment , où il est le plus élevé, le potentiel chimique diminue. Il augmente dans le compartiment , où il est le plus bas. Au cours de la migration, l'écart tend donc à diminuer.
La migration cesse lorsque les potentiels des deux compartiments sont égaux, soit , d'où . L'entropie ne varie plus et le système atteint un équilibre. Si la quantité continuait à diminuer, alors continuerait à diminuer et à augmenter, d'où et . De même, si la quantité augmentait à partir de cet équilibre, soit , alors augmenterait et diminuerait, d'où et . L'entropie globale , à partir de l'équilibre atteint, ne peut que diminuer, ce qui est contraire au deuxième principe de la thermodynamique : l'entropie a donc atteint un maximum et ne peut plus évoluer, cet équilibre est stable (voir la figure 1 avec ).

Si l'on considère une transformation à entropie constante (), alors :
Un raisonnement similaire à celui tenu à énergie constante montre que toute évolution de dans ces conditions à partir de l'équilibre (, d'où ) ne peut induire qu'une augmentation de l'énergie interne globale , soit , ce qui est contraire au premier principe de la thermodynamique : l'énergie interne a donc atteint un minimum, cet équilibre est stable (voir la figure 2 avec ).
Pour résumer, si deux compartiments sont mis en contact de telle sorte qu'ils ne puissent échanger que de la matière, une espèce chimique migre du compartiment dans lequel son potentiel chimique est le plus fort à celui de moindre potentiel. Le potentiel le plus fort diminue et le plus faible augmente. L'équilibre diffusif est atteint lorsque les deux potentiels s'égalisent. L'entropie du système a alors atteint un maximum et son énergie interne un minimum.
Équilibre de phases
Règle des phases

Les courbes représentent les équilibres de deux phases : si la température est fixée, la pression est subie, et réciproquement. Dans les domaines délimités par les courbes une seule phase est stable : on peut y faire varier la pression indépendamment de la température. Le point critique et le point triple ne peuvent être modifiés.
Soit un mélange quelconque composé de espèces chimiques réparties en phases. Les conditions d'équilibre stable d'un système hétérogène définies plus haut impliquent que :
- les pressions sont liées par les égalités :
- les températures sont liées par les égalités :
- pour chacun des constituants, les potentiels chimiques sont liés par les égalités :
Pour chaque phase, les diverses variables sont également liées par la relation de Gibbs-Duhem, soit équations supplémentaires :
On a donc un total de variables et équations. La variance indique le nombre de variables, c'est-à-dire le nombre de conditions opératoires (parmi la pression, la température et les compositions des phases), que l'opérateur peut fixer indépendamment l'une de l'autre en restant dans le domaine d'équilibre stable des phases, d'où la règle des phases[53] :
Par exemple, pour un corps pur, soit :
- en présence d'une seule phase (par exemple un liquide seul) , soit , on a : l'opérateur peut imposer la pression et la température indépendamment l'une de l'autre ;
- en présence de deux phases (par exemple un équilibre liquide-gaz), soit , on a : l'opérateur peut imposer la pression mais la température d'équilibre est subie (et inversement) ;
- en présence de trois phases (par exemple le point triple de l'équilibre solide-liquide-gaz), soit , on a : l'opérateur ne peut imposer aucune condition de l'équilibre.
Un mélange de constituants peut au plus se présenter sous phases à l'équilibre stable. Il ne peut y avoir au plus qu'une seule phase gaz, mais il peut y avoir plusieurs phases liquides et solides à l'équilibre[46].
L'entropie dans un changement d'état
On apporte, à pression et quantité de matière constantes, de la chaleur à un corps pur. Son énergie interne , en présence du travail des seules forces de pression, évolue selon :
En introduisant l'enthalpie , on a, à pression constante :
La transformation est réversible, on a par conséquent, avec l'entropie :
Les différentielles de deuxième ordre des deux fonctions sont données par (d2S) et (d2H) à pression et quantité de matière constantes :
La transformation ayant lieu à pression constante, on a par définition de la capacité thermique isobare :
La température thermodynamique est positive, et, selon (csCP), on a . En conséquence, avec (a) on obtient :
Les équations (a), (b) et (c) montrent que, à pression et composition constantes, l'entropie est une fonction croissante concave de l'enthalpie , qui est elle-même une fonction croissante convexe de l'entropie.

Sur la figure ci-contre, la courbe ABC bleue représente l'évolution, à pression et quantité de matière constantes, de l'entropie d'un corps pur solide, la courbe CDE orange celle du même corps pur liquide. Les deux courbes sont concaves : si l'on joint deux points bleus, ou deux points orange, par un segment de droite, celui-ci est en-dessous de la courbe considérée. Cependant, la courbe globale ABCDE n'est pas dérivable au point C. De plus, elle est localement convexe entre B et D : si l'on joint un point de BC à un point de CD par un segment de droite, celui-ci est au-dessus de la courbe. Entre les points B et D, le corps pur ne peut pas être en équilibre stable s'il suit la courbe BCD[54].
Pour conserver la concavité de l'entropie, le corps pur subit un changement d'état et l'entropie passe par le segment de droite BD gris. Au point B le segment gris est tangent à la courbe bleue du solide, au point D il est tangent à la courbe orange du liquide. La courbe ABDE est globalement dérivable et concave, contrairement à la courbe ABCDE. Le segment BD est la seule trajectoire qui rende l'entropie globalement dérivable et concave de A à E, tout autre point que B ou D, toute autre courbe qu'un segment de droite entre ces deux points engendrerait une courbe d'entropie localement non dérivable ou convexe. Aux basses enthalpies, en amont du point B, le corps pur est exclusivement solide. En aval du point D, aux hautes enthalpies, le corps pur est exclusivement liquide. Entre B et D, le corps pur fusionne et les deux phases, à enthalpie donnée, coexistent dans un équilibre stable[54].
Entre B et D l'entropie suit donc un segment de droite en fonction de l'enthalpie. La relation induit par conséquent que sur ce segment la température est constante, conformément à la règle des phases : puisque l'on travaille à pression constante, les deux phases du corps pur ne peuvent coexister qu'à une seule température . Ainsi, les grandeurs , , et sont établies aux mêmes pression, température et quantité de matière. La température de changement d'état (ici la température de fusion) est donnée par le rapport[54] :
L'écart rapporté à la quantité de matière totale mise en jeu est l'entropie de changement d'état du corps pur (ici l'entropie de fusion). L'écart rapporté à la quantité de matière totale mise en jeu est l'enthalpie de changement d'état du corps pur (ici l'enthalpie de fusion)[54]. L'enthalpie de changement d'état est la chaleur qu'il faut apporter à 1 mole de corps pur pour passer entièrement d'un état à l'autre.
L'équation du segment BD gris s'écrit :
Les points B et D représentant la même quantité de corps pur, on peut écrire, en introduisant les grandeurs molaires respectives :
Pour le corps pur est au point B (ici entièrement solide), pour il est au point D (ici entièrement liquide). Pour le corps pur est biphasique, entre B et D : une quantité de phase B coexiste dans un équilibre stable avec une quantité de phase D. Le paramètre est le taux de changement d'état (ici le taux de fusion), c'est-à-dire la quantité de phase D (ici de liquide) rapportée à la quantité de matière totale (ici le total de solide et de liquide) mise en jeu lors de la transformation. Autrement dit, si l'on dispose d'une part d'une quantité de corps pur à l'état B et que l'on en prélève une fraction , et d'autre part d'une quantité de corps pur à l'état D et que l'on en prélève une fraction , si l'on met en contact ces deux fractions, alors celles-ci sont d'emblée en équilibre stable, sans nécessité d'une transformation pour atteindre cet équilibre (voir la section Concavité de l'entropie)[55].
Les branches BC bleue et CD orange sont des branches de métastabilité des phases correspondantes. Si le corps pur évolue sur ces branches (y compris au-delà de C pour le solide, et en deçà de C pour le liquide), la moindre perturbation peut provoquer un brusque changement d'état, amenant l'entropie sur la courbe ABDE stable, à enthalpie constante[54]. L'état métastable du liquide non solidifié en dessous de sa température de fusion est appelé « surfusion », il s'observe de façon naturelle lors des pluies verglaçantes (voir également la vidéo présentée dans la section Équilibre stable). L'état métastable du liquide non vaporisé au-dessus de sa température d'ébullition est appelé « surébullition » ou « retard à l'ébullition », il peut s'observer dans une tasse de café chauffé au microonde qui entre en ébullition brutale lorsque l'on y ajoute du sucre[56].
Le même raisonnement peut être tenu pour tout autre changement d'état du corps pur. Il est similaire pour les changements d'état des mélanges.
Équilibre chimique
Conditions de l'équilibre chimique
Soit un système fermé siège d'une réaction chimique. Son énergie interne varie selon :
avec :
- l'affinité chimique ; ;
- l'avancement de réaction.
Pour un système isolé, à et constants, l'équilibre chimique :
- évolue selon ;
- est atteint lorsque :
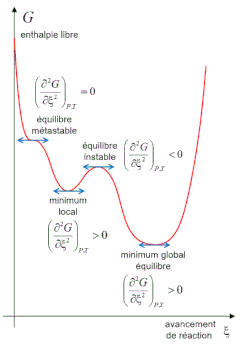
L'enthalpie libre de réaction vaut , l'opposé de l'affinité chimique. On a : .
Pour un système fermé contraint, les divers potentiels thermodynamiques donnent, selon les conditions opératoires :
- à volume et entropie constants :
- une évolution selon ;
- à l'équilibre stable et ;
- à volume et température constants :
- une évolution selon ;
- à l'équilibre stable et ;
- à pression et entropie constantes :
- une évolution selon ;
- à l'équilibre stable et ;
- à pression et température constantes :
- une évolution selon ;
- à l'équilibre stable et .
Quelles que soient les conditions opératoires, la réaction chimique évolue donc selon :
On note et les deux conditions opératoires laissées constantes. La seule variable de laissée libre est . On a par conséquent :
Ainsi, quelles que soient les conditions opératoires et maintenues constantes, on a à l'équilibre[57],[58] :
Déplacement de l'équilibre
Soit un milieu réactionnel à l'équilibre. On modifie l'une des conditions du mélange réactionnel (pression, température, quantité de l'un des constituants, etc.) en considérant dans un premier temps que toutes les autres conditions du milieu restent constantes. Soit la variable conjuguée[32] de :
La fonction est le potentiel thermodynamique dont les sont les variables naturelles, celles-ci incluant la variable modifiée et l'avancement de réaction . En l'absence de réaction, soit à constant, le système évolue selon (voir la section Conclusions générales) :
Le milieu réactionnel étant initialement à l'équilibre, son affinité chimique initiale est nulle : . La modification de induit la variation de l'affinité : . L'affinité chimique est l'opposé de la dérivée partielle du potentiel thermodynamique selon l'avancement de réaction : . Le théorème de Schwarz donne :
On note la variation de due à la réaction dans les conditions constantes :
On a par conséquent :
Après modification de , en l'absence de réaction, l'affinité chimique devient donc . L'équilibre se déplace ensuite selon le sens dicté par le deuxième principe de la thermodynamique : , d'où . On obtient finalement :
On en déduit que, par la réaction :
- une augmentation de , soit , induit une diminution de : ;
- une diminution de , soit , induit une augmentation de : .
Par conséquent :
| La modification d'une variable quelconque déplace la réaction dans le sens impliquant une variation opposée de sa variable conjuguée[32] . |
On modifie la condition d'un milieu réactionnel initialement à l'équilibre. Le système évolue à la fois par cette modification externe et par le déplacement interne de l'équilibre chimique, jusqu'à atteindre un nouvel équilibre. Les conditions opératoires laissées constantes tout au long de ce processus sont les variables de communes aux deux ensembles et , soit . Lorsque l'on modifie , la variation totale de sa variable conjuguée vaut par conséquent[59] :
On en déduit que[59],[60],[61] :
- si est intensive, sa variable conjuguée est extensive :
- une augmentation de , soit , induit que et ;
- une diminution de , soit , induit que et ;
- la variation de est plus importante avec la réaction que sans la réaction : ;
- si est extensive, sa variable conjuguée est intensive :
- une augmentation de , soit , induit que et ;
- une diminution de , soit , induit que et ;
- la variation de est moins importante avec la réaction que sans la réaction : .
| La modification d'une variable intensive induit une variation de sa variable conjuguée[32] extensive plus grande avec la réaction que sans la réaction. Autrement dit, la modification de déplace l'équilibre dans le sens qui amplifie la modification de [59],[60],[61]. |
| La modification d'une variable extensive induit une variation de sa variable conjuguée intensive plus petite avec la réaction que sans la réaction. Autrement dit, la modification de déplace l'équilibre dans le sens qui s'oppose à la modification de [59],[60],[61]. |
Applications courantes
Le tableau suivant résume les modifications de conditions opératoires les plus courantes d'un équilibre chimique[62].
| Variable modifiée | Conditions opératoires constantes | Variable conjuguée | Sans la réaction | Par la réaction | Variation globale avec la réaction et sans la réaction |
|---|---|---|---|---|---|
| (edeP) | (csF1) | ||||
| (edeV) | (csG1) | ||||
| (edeS) | (csF2) | ||||
| (edeS) | (csG2) | ||||
| (mu) | (csF3) | ||||
| (mu) | (csG3) |
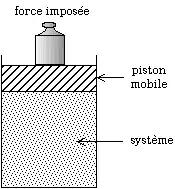
Modification du volume par déplacement du piston. Si l'on diminue le volume, la pression augmente moins avec la réaction que sans la réaction. Pour obtenir une certaine pression, il faut donc diminuer plus fortement le volume avec la réaction que sans la réaction.
Modification de la pression par les poids posés sur le piston. Si l'on augmente la pression, le volume diminue plus avec la réaction que sans la réaction. Pour obtenir un certain volume, il faut donc appliquer une pression moins forte avec la réaction que sans la réaction.
Exemple 1 - Modification du volume à température constante.
- Si l'on augmente le volume, soit , à température constante, on a :
- sans la réaction, une diminution de la pression : ;
- par la réaction, une augmentation de la pression : ;
- la variation globale de la pression : .
- Si l'on augmente le volume à température constante, la pression diminue moins avec la réaction que sans la réaction. Inversement, si l'on diminue le volume, la pression augmente moins avec la réaction que sans la réaction. Lorsque l'on modifie le volume (grandeur extensive), la réaction s'oppose à la modification de la pression (grandeur intensive).
Exemple 2 - Modification de la pression à température constante.
- Si l'on augmente la pression à température constante, le volume diminue plus avec la réaction que sans la réaction. Inversement, si l'on diminue la pression, le volume augmente plus avec la réaction que sans la réaction. Lorsque l'on modifie la pression (grandeur intensive), la réaction amplifie la modification du volume (grandeur extensive).
Exemple 3 - Modification de la température.
- Si l'on augmente la température à pression constante ou volume constant, l'entropie du système augmente plus avec la réaction que sans la réaction. Inversement, si l'on diminue la température, l'entropie diminue plus avec la réaction que sans la réaction. Lorsque l'on modifie la température (grandeur intensive), la réaction amplifie la modification de l'entropie du milieu réactionnel (grandeur extensive), c'est-à-dire l'échange de chaleur du milieu réactionnel avec l'extérieur.
- Une réaction qui augmente l'entropie du milieu réactionnel, soit , absorbe de la chaleur, elle est endothermique. Une réaction qui diminue l'entropie, soit , dégage de la chaleur, elle est exothermique. Lorsque l'on chauffe un milieu réactionnel pour atteindre une certaine température, il faut donc lui fournir plus de chaleur avec la réaction que sans la réaction, car la réaction absorbe une partie de la chaleur fournie. Si l'on fournit une certaine quantité de chaleur au milieu réactionnel, la température obtenue est moins élevée avec la réaction que sans la réaction. En augmentant la température, l'équilibre se déplace dans le sens endothermique : il amplifie l'absorption de chaleur et semble ainsi s'opposer à la modification de la température. Il s'agit de la loi de van 't Hoff.
Exemple 4 - Modification de la composition.
- Si l'on augmente la quantité d'un constituant (réactif, produit ou inerte), que ce soit à volume et température constants, ou à pression et température constantes, le potentiel chimique de ce constituant augmente moins avec la réaction que sans la réaction. Inversement, si l'on diminue la quantité d'un constituant, le potentiel chimique de ce constituant diminue moins avec la réaction que sans la réaction. Lorsque l'on modifie la quantité d'un constituant quelconque du milieu réactionnel (grandeur extensive), la réaction s'oppose à la modification du potentiel chimique de cette espèce (grandeur intensive).
- Ceci n'implique pas que la réaction se déplace dans le sens qui consomme le constituant ajouté et diminue sa quantité. Il existe en effet des cas où la réaction se déplace dans le sens qui produit le constituant ajouté et augmente donc sa quantité, son potentiel chimique étant néanmoins diminué[63].
Thermodynamique des surfaces
Surface minimale

On considère un système fermé séparé de l'extérieur par une interface formant une surface d'aire (par exemple une bulle de gaz dans un liquide). Lorsque l'on déforme cette interface, le travail de la force exercée sur sa surface vaut . La tension superficielle est une grandeur positive[64] : on doit fournir un travail au système pour agrandir sa surface. Ce travail est généralement négligeable et négligé devant le travail des forces de pression. À composition constante, l'énergie interne du système varie selon :
On a donc la condition d'évolution du système à composition constante :
| Condition d'évolution |
La tension superficielle peut ainsi être définie indifféremment par[65] :
| Tension superficielle |

Quelles que soient les conditions opératoires considérées, le système évolue donc selon : la surface de l'interface ne peut que décroître. À l'équilibre stable atteint un minimum. Toute variation d'un paramètre de l'équilibre ne peut alors que faire croître , soit ; par conséquent, à partir de l'équilibre : la surface de l'interface ne peut que croître. Quelles que soient les conditions opératoires, on a donc[66] :
| À l'équilibre thermodynamique stable, la surface de l'interface entre le système et l'extérieur est minimale. |
Une bulle de gaz dans un liquide est donc sphérique (si sa vitesse de déplacement est faible, sinon elle se déforme), de même qu'une gouttelette de liquide dans un aérosol. Un liquide dans un verre forme une interface plane avec l'air. Si l'on déforme ces interfaces, leur surface augmente. Puis, lorsque l'on supprime la perturbation, la surface tend à reprendre sa forme initiale, minimale.
La coalescence

Soit un système composé d'une phase dispersée dans une autre phase (l'extérieur). Ce système comporte un ensemble de sous-systèmes notés , de tailles variées et à l'équilibre entre eux. Chaque sous-système est caractérisé par un volume , une surface , une entropie et les quantités des constituants . Ces sous-systèmes sont aux mêmes pression , température et composition (fractions molaires), d'où pour chaque constituant le même potentiel chimique dans chacun des sous-systèmes. Puisque l'énergie interne est extensive, la variation d'énergie interne globale du système est la somme des variations d'énergie interne des sous-systèmes :
On pose le volume total du système , sa surface totale , son entropie et l'enthalpie libre . La quantité globale de chacun des constituants est invariante :

On a finalement, à pression, température et composition constantes, la condition d'évolution de la phase dispersée :
Note : le même raisonnement mené non pas à pression constante mais à volume constant, soit , conduit à l'étude de l'énergie libre à la place de . Les conclusions suivantes restent identiques.
La surface globale du système ne peut que décroître. En conséquence, lorsque deux sous-systèmes initialement séparés, de surfaces et quelconques, fusionnent pour ne plus en former qu'un, la surface du système résultant est, à l'équilibre, inférieure à la somme des deux surfaces initiales, soit . Deux gouttes d'eau sphériques qui fusionnent donnent une nouvelle goutte sphérique ; le volume est conservé, mais la surface diminue.
Ceci explique la tendance des milieux dispersés (émulsions, aérosols, mousses, etc.) à la coalescence : ils sont instables par nature. Les sous-systèmes, bulles ou gouttes, fusionnent spontanément, ce phénomène accroît l'entropie et diminue l'énergie du milieu en diminuant sa surface. Dans un empilement de bulles de savon (une mousse), les parois internes tendent à se rompre afin de ne former qu'une seule bulle. Dans une vinaigrette (une émulsion), les gouttelettes d'huile dispersées dans la phase aqueuse tendent spontanément à fusionner jusqu'à ne plus former qu'une seule phase continue : l'huile et la phase aqueuse se séparent pour atteindre l'équilibre[67].
Notations et outils mathématiques
Notations
- Alphabet latin
- l'affinité chimique ;
- la surface ;
- l'énergie libre ;
- l'enthalpie libre ;
- l'enthalpie ;
- le nombre d'espèces chimiques différentes dans le système ;
- la quantité de l'espèce chimique ;
- la pression ;
- la chaleur ;
- l'entropie du système thermodynamique étudié ;
- l'entropie de l'extérieur ;
- la température thermodynamique ;
- l'énergie interne du système thermodynamique étudié ;
- l'énergie interne de l'extérieur ;
- le volume du système thermodynamique étudié ;
- le volume de l'extérieur ;
- le travail ;
- une grandeur molaire ;
- une grandeur molaire partielle liée à l'espèce chimique ;
- , , des variables quelconques.
- Alphabet grec
- la tension superficielle ;
- l'avancement de réaction ;
- le potentiel chimique de l'espèce chimique ;
- , des fonctions quelconques ;
- la dérivée partielle de par rapport à la variable ;
- la dérivée partielle seconde de par rapport aux variables et .
Différentielles et dérivées des fonctions thermodynamiques
Série de Taylor
Soit une fonction quelconque, dont les variables sont :
On suppose cette fonction au moins fois dérivable par rapport à chacune de ses variables. Selon le théorème de Taylor, on peut poser en tout point , pour tout ensemble de variations élémentaires quelconques[68] :
Dans cette expression est la différentielle d'ordre de au point avec les variations élémentaires :
Le terme est la dérivée partielle d'ordre de la fonction par rapport à ses variables calculée au point .
On suppose que toutes les fonctions thermodynamiques, entropie et potentiels thermodynamiques , , et , sont au moins deux fois dérivables par rapport à l'ensemble de leurs variables.
Différentielle du premier ordre
La différentielle du premier ordre d'une fonction quelconque s'écrit[68],[69] :
On note toute dérivée partielle du premier ordre[69] :
on obtient :
Les différentielles du premier ordre des fonctions thermodynamiques s'écrivent, dans leurs variables naturelles :
- entropie :
- énergie libre :
- Notes
- La pression , la température et les potentiels chimiques sont des grandeurs intensives. Les fonctions , , , et , le volume et les quantités sont des grandeurs extensives.
- Les variables de l'entropie et celles de l'énergie interne sont toutes extensives.
- Dans le cas de l'entropie , les grandeurs sont intensives et le produit est homogène à une entropie : et sont « conjuguées par rapport à l'entropie ». Dans le cas des potentiels thermodynamiques , , et , les grandeurs et sont « conjuguées par rapport à l'énergie » : l'une des deux est extensive et l'autre intensive, et leur produit est homogène à une énergie[32].
Transformation de Legendre
Soit une fonction quelconque, dont les variables naturelles sont et :
avec :
On pose :
Soit la transformée de Legendre de telle que[70],[71] :
On a par conséquent :
La nouvelle fonction dépend de et des [70] :
Avec :
on obtient :
On pose [70]. On a et pour toute fonction et . Les tableaux suivants résument les relations entre les principaux potentiels thermodynamiques[70],[71].
| Potentiel | Potentiel | Variable | Variable | Variables communes |
|---|---|---|---|---|
| Énergie interne | Énergie libre | |||
| Énergie interne | Enthalpie | |||
| Énergie libre | Enthalpie libre | |||
| Enthalpie | Enthalpie libre |
- Notes
- Les transformées de Legendre de l'entropie sont les fonctions de Massieu.
- L'enthalpie libre est le résultat d'une double transformation de Legendre : .
- Les variables et sont conjuguées : l'une est extensive, l'autre est intensive, et leur produit est homogène à une énergie.
- Les variables naturelles de l'énergie interne sont toutes extensives. La transformation de Legendre remplace une variable extensive de par une variable intensive d'un autre potentiel : remplacement du volume de par la pression de et , remplacement de l'entropie de par la température de et .
| Potentiel | Relation | |
|---|---|---|
| Équations d'état | Potentiel chimique | |
| (edeP) | ||
| (edeT) | ||
| (edeS) | ||
| (edeV) | ||
- Notes
- Les équations d'état sont des relations définissant la pression (edeP), la température (edeT), l'entropie (edeS) et le volume (edeV) en tant que dérivées partielles des potentiels thermodynamiques.
- Le potentiel chimique de l'espèce chimique est défini indifféremment par :
Différentielle du deuxième ordre
La différentielle du deuxième ordre d'une fonction quelconque s'écrit[68],[72] :
On note toute dérivée partielle du deuxième ordre[72] :
d'où :
Le théorème de Schwarz permettant d'écrire, pour toutes variables et [72],[73] :
on obtient[72] :
On a par ailleurs la différentielle pour toute variable , en fonction des variables de :
on obtient :
Les différentielles du deuxième ordre des fonctions thermodynamiques s'écrivent, dans leurs variables naturelles :
- entropie (d2S) :
- énergie interne (d2U) :
- énergie libre (d2F) :
- enthalpie (d2H) :
- enthalpie libre (d2G) :
- Notes
- Avec et une autre variable quelconque, on a pour toute fonction :
- ;
- , d'où ; les conditions de stabilité n'imposent pas le signe de ces dérivées croisées ;
- , d'où ; a la même convexité par rapport à et .
- Il est donc indifférent de travailler avec ou pour déterminer la convexité de la fonction .
Critères de convexité - stabilité
Convexité et extrémums
Une fonction est convexe si sa matrice hessienne est définie positive en tout point. Entre autres méthodes, il suffit de montrer que, quelles que soient les valeurs des variables et leurs variations élémentaires , on a[16] :
Cette forme quadratique selon les est la différentielle d'ordre deux de , d'où[16] :
Si est concave, sa matrice hessienne est définie négative, d'où[16] :
Les conditions de stabilité établies ci-après à partir de ces formes quadratiques ne sont nécessaires et suffisantes, pour démontrer que la matrice hessienne est définie positive ou négative, que dans les cas de fonctions à une ou deux variables. Pour les fonctions à plus de deux variables elles ne sont que nécessaires, elles ne sont pas suffisantes.
Lorsque l'équilibre thermodynamique est atteint, la différentielle du premier ordre . Le signe de la différentielle de deuxième ordre donne la nature de l'extrémum atteint : maximum si négatif, minimum si positif. Si est nulle, il est nécessaire d'étudier les différentielles d'ordre supérieur ; ce cas n'est pas traité ici, toutefois :
- s'il existe entier naturel non nul tel que , toutes les différentielles d'ordre inférieur étant nulles, alors :
- si , alors est concave, l'extrémum est un maximum ;
- si , alors est convexe, l'extrémum est un minimum ;
- s'il existe entier naturel non nul tel que , quel que soit son signe, toutes les différentielles d'ordre inférieur étant nulles, alors le point est un point d'inflexion, l'équilibre est métastable ;
- si quel que soit entier naturel non nul , alors l'équilibre est neutre, indifférent à toute modification de ses conditions d'établissement.
Comparaison de convexités
Soient deux potentiels thermodynamiques et liés par une transformation de Legendre : . On a les différentielles du deuxième ordre :
Avec les relations , et (voir la section Transformation de Legendre), on obtient :
Si l'on connait le signe de , alors on connait le signe de sous certaines conditions. Pour cela, on fixe certaines variables de :
- à constantes, soit pour tout :
- Dans ces conditions les deux différentielles du deuxième ordre sont de signes opposés. La transformation de Legendre inverse la convexité de la fonction : si est convexe par rapport à sa variable , alors est concave par rapport à sa variable ;
- à constante, soit :
- Dans ces conditions les deux différentielles du deuxième ordre sont de même signe. Si est convexe par rapport à ses variables , alors l'est aussi, ces variables étant communes aux deux potentiels.
Si est convexe par rapport à toutes ses variables, alors est concave par rapport à la variable transformée et convexe par rapport aux variables communes , elle est convexe-concave. Pour une variable commune quelconque, les autres variables étant fixées, on a et . Si l'on connait le signe de , on ne peut en déduire celui de , qui est donc indéterminé dans ces conditions.
Les conditions de stabilité par rapport aux potentiels thermodynamiques , et s'obtiennent en comparant leur différentielle du deuxième ordre à celle de l'énergie interne que l'on sait convexe par rapport à toutes ses variables naturelles, soit . Pour un potentiel thermodynamique quelconque, il suffit de trouver dans quelles conditions . Les variables de l'énergie interne sont toutes extensives. La transformation de Legendre remplace une variable extensive de par une variable intensive de . En conséquence, les potentiels thermodynamiques sont tous concaves par rapport à leur(s) variable(s) intensive(s)[22],[23]. Les autres variables communes à et sont donc extensives. En conséquence, les potentiels thermodynamiques sont tous convexes par rapport à leurs variables extensives[22],[23].
Fonction convexe
Soit une fonction quelconque convexe par rapport à sa seule variable (toutes ses autres variables étant fixées, ) :
On obtient immédiatement la condition de stabilité :
Pour une fonction quelconque convexe par rapport à ses deux variables et (toutes ses autres variables étant fixées, ) :
- ;
- (théorème de Schwarz)
À constant on a et par conséquent la condition de stabilité . Le même raisonnement mené à constant conduit à la condition de stabilité . Par ailleurs, quelles que soient les variations élémentaires et , la différentielle ne peut pas prendre de valeur négative. On pose[74],[75] :
- ; ; ;
Le polynôme du second degré caractéristique ainsi obtenu ne peut avoir que des valeurs positives ou nulles. Il ne peut avoir par conséquent que des racines complexes (le polynôme ne s'annule jamais avec des valeurs de réelles) ou une racine réelle double (le polynôme s'annule et atteint simultanément un minimum à une racine réelle double). Son discriminant répond donc à la contrainte . On obtient la condition de stabilité : . Ce résultat est indépendant du choix de ou . Cette condition ne renseigne pas sur le signe de la dérivée croisée , mais elle donne une indication sur sa valeur absolue : . Par le théorème de Schwarz cette condition est identique pour . Pour une fonction convexe par rapport à deux variables, on a donc les conditions de stabilité (théorème de Monge)[74],[76],[75] :
Pour une fonction convexe par rapport à plus de deux variables, on revient au cas à deux variables en fixant les variables surnuméraires.
Les potentiels thermodynamiques , , et sont tous convexes par rapport à leurs variables extensives[22]. Les variables de l'énergie interne sont toutes extensives.
Fonction concave
Le raisonnement pour une fonction concave est similaire à celui pour une fonction convexe. Sa différentielle du deuxième ordre ne peut avoir que des valeurs négatives ou nulles.
Pour une fonction concave par rapport à une seule variable, on a :
Pour une fonction concave par rapport à deux variables et plus, on a (théorème de Monge)[74],[76],[75] :
La dernière condition sur les dérivées croisées est identique à celle de la fonction convexe : elle impose que le polynôme caractéristique ne puisse changer de signe.
L'entropie est concave par rapport à toutes ses variables, qui sont toutes extensives. Les potentiels thermodynamiques , et sont concaves par rapport à leurs variables intensives (l'énergie interne n'en a pas).
Fonction convexe-concave
Il est toujours possible de déterminer le signe de la dérivée seconde d'une fonction thermodynamique (entropie ou potentiel thermodynamique) ; on sait donc si la fonction est convexe ou concave par rapport à cette seule variable .
Si est convexe par rapport à , soit , et concave par rapport à , soit , alors la fonction est convexe-concave. Le polynôme caractéristique doit pouvoir changer de signe et son discriminant est tel que . On obtient[74] :
Cette dernière condition ne renseigne ni sur le signe, ni sur la valeur absolue de , puisque et .
Ce cas est rencontré si est extensive et intensive, pour les potentiels thermodynamiques énergie libre , enthalpie et enthalpie libre .
Établissement des critères de stabilité
Les conditions établies ci-après ne sont nécessaires et suffisantes, pour établir la stabilité du système thermodynamique, que dans le cas de transformations n'impliquant qu'une seule ou deux variables thermodynamiques. Pour des transformations impliquant plus de variables, elles ne sont que nécessaires à la stabilité, elles ne sont pas suffisantes.
Critères selon l'entropie
La relation (d2S) donne, à composition constante, soit pour toute espèce chimique :
En conséquence, étant donné la concavité de l'entropie, soit , on obtient immédiatement[55],[77] :
En considérant tous les autres jeux de deux variables possibles de , on obtient de la même façon, pour toutes espèces chimiques et :
L'entropie est concave par rapport à ses variables , et , qui sont toutes extensives[76].
Critères selon l'énergie interne
La relation (d2U) donne, à composition constante, soit pour toute espèce chimique :
En conséquence, étant donné la convexité de l'énergie interne, soit , on obtient immédiatement[55],[78] :
En considérant tous les autres jeux de deux variables possibles de , on obtient de la même façon, pour toutes espèces chimiques et :
L'énergie interne est convexe par rapport à ses variables , et , qui sont toutes extensives[76].
Critères selon l'énergie libre
Les relations (d2F) et (d2U) donnent, à température constante, soit :
On obtient immédiatement, pour toutes espèces chimiques et [79],[80] :
À volume et composition constants, soit et pour toute espèce chimique :
On obtient immédiatement[79],[80] :
L'énergie libre est convexe par rapport à ses variables extensives et , et concave par rapport à sa variable intensive ; on n'a donc aucune condition de stabilité concernant et [76].
Critères selon l'enthalpie
Les relations (d2H) et (d2U) donnent, à pression constante, soit :
On obtient immédiatement, pour toutes espèces chimiques et [80] :
À entropie et composition constantes, soit et pour toute espèce chimique :
On obtient immédiatement[80] :
L'enthalpie est convexe par rapport à ses variables extensives et , et concave par rapport à sa variable intensive ; on n'a donc aucune condition de stabilité concernant et [76].
Critères selon l'enthalpie libre
Les relations (d2G) et (d2U) donnent, à pression et température constantes, soit et :
On obtient immédiatement, pour toutes espèces chimiques et [43] :
À composition constante, soit pour toute espèce chimique :
On obtient immédiatement[81],[80],[82] :
L'enthalpie libre est convexe par rapport à ses variables extensives et concave par rapport à ses variables intensives et ; on n'a donc aucune condition de stabilité concernant et [76].
Notes et références
Notes
- 1 2 3 4 Callen 1991, p. 13-15.
- 1 2 3 4 5 6 Taillet et al. 2018, p. 273-274.
- 1 2 Greiner et al. 1999, p. 7.
- 1 2 3 4 5 6 7 Infelta et al. 2006, p. 1-4.
- ↑ Taillet et al. 2018, p. 706.
- ↑ Jean Briant, Phénomènes d'interface. Agents de surface : principes et modes d'action, Technip, , 340 p. (ISBN 9782710805786, lire en ligne), p. 35.
- ↑ Lucien Borel et Daniel Favrat, Thermodynamique et énergétique : De l'énergie à l'exergie, vol. 1, PPUR presses polytechniques, , 814 p. (ISBN 9782880745455, lire en ligne), p. 10-11.
- ↑ Taillet et al. 2018, p. 689.
- ↑ Pierre Infelta et Michael Graetzel, Thermodynamique : Principes et Applications, Boca Raton, Floride, BrownWalker Press, , 484 p. (ISBN 1-58112-995-5, lire en ligne), p. 36.
- ↑ Michel Feidt, Génie énergétique : Du dimensionnement des composants au pilotage des systèmes, Dunod, , 976 p. (ISBN 9782100708635, lire en ligne), p. 141.
- 1 2 Mines-ParisTech, « Deuxième principe », sur direns.mines-paristech.fr (consulté le ).
- 1 2 Daniel Fargue, Abrégé de thermodynamique : principes et applications, Presses des Mines, coll. « Les Cours », , 242 p. (ISBN 9782911762499, lire en ligne), p. 21-22.
- 1 2 Michel Feidt, Génie énergétique : Du dimensionnement des composants au pilotage des systèmes, Dunod, , 976 p. (ISBN 9782100708635, lire en ligne), p. 138-139.
- 1 2 3 4 5 6 Prestipino et al. 2003, p. 481-482.
- 1 2 3 4 5 6 Georges Gonczi, Comprendre la thermodynamique avec des exercices résolus et commentés : Licence, CPGE, Éditions Ellipses, , 2e éd., 288 p. (ISBN 9782340051706, lire en ligne), p. 93-95.
- 1 2 3 4 5 6 7 Caulier et al. 2018, p. 157-158.
- ↑ Taillet et al. 2018, p. 141.
- 1 2 Galgani et al. et 2009 p.230-231.
- ↑ Callen 1991, p. 203.
- ↑ Callen 1991, p. 38.
- ↑ Galgani et al. et 2009 p.231-232.
- 1 2 3 4 5 6 Galgani et al. et 2009 p.232-233.
- 1 2 3 4 5 6 Chen 2021, p. 168.
- ↑ Taillet et al. 2018, p. 461.
- ↑ Peliti 2011, p. 24-25.
- ↑ Chen 2021, p. 151-153.
- ↑ Greiner et al. 1999, p. 98.
- 1 2 Chen 2021, p. 153-154.
- ↑ Chen 2021, p. 155-156.
- ↑ Chen 2021, p. 154-155.
- ↑ Chen 2021, p. 156-157.
- 1 2 3 4 5 6 La variable conjuguée de s'entend ici au sens de dérivée partielle du potentiel thermodynamique par rapport à la variable , ce qui implique de tenir compte du signe de cette dérivée. Ainsi, au sens de l'énergie interne, la variable conjuguée de l'entropie est la température, selon (edeT). Mais au sens de l'énergie libre, la variable conjuguée de la température est l'opposé de l'entropie, selon (edeS).
- ↑ (en) J. P. O'Connell et J. M. Haile, Thermodynamics : Fundamentals for Applications, Cambridge University Press, , 654 p. (ISBN 9781139443173, lire en ligne), p. 93.
- ↑ Jean-Noël Foussard, Edmond Julien, Stéphane Mathé et Hubert Debellefontaine, Thermodynamique : Applications aux systèmes physicochimiques, Dunod, (ISBN 978-2-10-072894-7, lire en ligne), p. 13.
- 1 2 3 4 Callen 1991, p. 210.
- 1 2 3 4 Bonnefoy 2016, p. 50.
- ↑ Roger Balian, « Pourquoi le Soleil n’explose pas, ou les bienfaits d'une chaleur spécifique négative », Reflets de la physique, Société française de physique, no 10, , p. 14-15 (lire en ligne [PDF], consulté le ).
- ↑ A. Fortes et al., « Compressibilité négative », La Recherche, no 451, (lire en ligne).
- ↑ Maurice Mashaal, « Un matériau aux propriétés contre-intuitives », Pour la science, (lire en ligne).
- ↑ (en) Andrew B. Cairns, Jadna Catafesta, Claire Levelut et Jérôme Rouquette, « Giant negative linear compressibility in zinc dicyanoaurate », Nature Materials, vol. 12, no 3, , p. 212–216 (ISSN 1476-4660, DOI 10.1038/nmat3551, lire en ligne, consulté le ) (résumé en français).
- ↑ Le Bellac et al. 2004, p. 31.
- ↑ Cette anomalie a été utilisée en 1901 par le Bureau international des poids et mesures (BIPM) pour définir le litre comme « le volume occupé par la masse de 1 kilogramme d'eau pure, à son maximum de densité et sous la pression atmosphérique normale ». Cette définition fut abrogée en 1964, voir l'article Litre.
- 1 2 Pierre Desré et Fiqiri Hodaj, Thermodynamique des matériaux, EDP Sciences, coll. « Sciences des matériaux », , 408 p. (ISBN 9782759809288, lire en ligne), p. 47-48.
- 1 2 3 4 5 6 Greiner et al. 1999, p. 57-58.
- ↑ Jean-Luc Godet, Université d'Angers - Numéliphy, « Fonctions thermodynamiques et potentiels chimiques : Équilibre entre phases et potentiel chimique », sur res-nlp.univ-lemans.fr (consulté le ).
- 1 2 Exemple de sept phases liquides (heptane, aniline, eau, perfluorokérosène, phosphore, gallium, mercure) en équilibre à pression et température ambiantes : (en) Joel H. Hildebrand, « Seven Liquid Phases in Equilibrium. », Journal of Physical Chemistry, vol. 53, no 6, , p. 944-947 (lire en ligne).
- ↑ Informations lexicographiques et étymologiques de « diatherme » dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales.
- ↑ « Diatherme », dictionnaire Larousse.
- ↑ Taillet et al. 2018, p. 597.
- 1 2 (en) M.W. Collins, R.C. Dougal, C. Koenig et I. Ruddock, Kelvin, Thermodynamics and the Natural World, vol. 10, Witt Press, coll. « Design and Nature », , 482 p. (ISBN 9781845641498, lire en ligne), p. 331.
- ↑ Lucien Borel et Daniel Favrat, Thermodynamique et énergétique, vol. 1, PPUR presses polytechniques, , 814 p. (ISBN 9782880745455, lire en ligne), chapitre 1.2 Principe zéro de la thermodynamique, p. 8-11.
- ↑ (en) Mark W. Zemansky et Richard H. Dittman, Heat and Thermodynamics : An Intermediate Textbook, McGraw-Hill, , 7e éd., 487 p. (ISBN 0-07-017059-2, lire en ligne [PDF]), p. 295-297.
- ↑ Taillet et al. 2018, p. 559.
- 1 2 3 4 5 6 Jean-Pierre Provost et Gérard Vallée, Les maths en physique : La physique à travers le filtre des mathématiques (avec éléments d'analyse numérique), Dunod, , 384 p. (ISBN 9782100559336, lire en ligne), p. 141-143.
- 1 2 3 Prestipino et al. 2003, p. 482.
- ↑ M'hamed Ali Chaker, Yassine Khalsi et Hager Ben Mahmoud, Olympiades Nationales de Chimie, « Expérience 1 : l'eau surchauffée au four à micro-ondes. » [vidéo], sur youtube.com, (consulté le ).
- ↑ Jean-Claude Legrand, Thermodynamique chimique : les applications, Bréal, coll. « L'indispensable », (ISBN 978-2-7495-2241-8, lire en ligne), p. 85.
- ↑ Michel Soustelle, Équilibres chimiques, vol. 4, Londres, ISTE Group, coll. « Génie des procédés / Thermodynamique chimique approfondie », 2015b, 196 p. (ISBN 978-1-78405-103-7, lire en ligne), p. 62.
- 1 2 3 4 Liénard 1944, p. 38-57.
- 1 2 3 (en) J. De Heer, « The Principle of Le Châtelier and Braun », Journal of Chemical Education, vol. 34, no 8, , p. 375-380 (DOI 10.1021/ed034p375).
- 1 2 3 Callen 1991, p. 210-214.
- ↑ Liénard 1944, p. 45.
- ↑ Soustelle 2015b, p. 39-43.
- ↑ Soustelle 2016, p. 28.
- ↑ Michel Soustelle, Thermodynamique des surfaces et des systèmes capillaires, vol. 7, Londres, ISTE Group, coll. « Génie des procédés / Thermodynamique chimique approfondie », , 1re éd., 240 p. (ISBN 9781784051549, lire en ligne), p. 21-25.
- ↑ Soustelle 2016, p. 28-29.
- ↑ Encyclopædia Universalis, « Colloïdes », sur universalis.fr (consulté le ).
- 1 2 3 Bonnefoy 2016, p. 90.
- 1 2 Jean-François Caulier et Laurent Braquet, Mathématiques économiques, De Boeck Supérieur, coll. « Sup en Poche Éco », , 256 p. (ISBN 9782807315518, lire en ligne), Fiches 11 et 12, p. 144-146.
- 1 2 3 4 Infelta et al. 2006, p. 449-450.
- 1 2 Bonnefoy 2016, p. 24-28.
- 1 2 3 4 Caulier et al. 2018, p. 147-148.
- ↑ Bonnefoy 2016, p. 90-91.
- 1 2 3 4 Caulier et al. 2018, p. 160-162.
- 1 2 3 Bonnefoy 2016, p. 92.
- 1 2 3 4 5 6 7 Le Bellac et al. 2004, p. 27-30.
- ↑ Callen 1991, p. 204-206.
- ↑ Callen 1991, p. 207.
- 1 2 Prestipino et al. 2003, p. 488.
- 1 2 3 4 5 Callen 1991, p. 208.
- ↑ Prestipino et al. 2003, p. 490.
- ↑ Callen 1991, p. 209.
Articles
- (en) L. Galgani et A. Scotti, « On Subadditivity And Convexity Properties Of Thermodynamic Functions », Pure and Applied Chemistry, vol. 22, nos 3-4, (DOI 10.1351/pac197022030229, lire en ligne [PDF], consulté le ).
- Alfred-Marie Liénard, « Thermodynamique. Quelques particularités des déplacements de l’équilibre et stabilité », Annales de la faculté des sciences de Toulouse, 4e série, t. 8, , p. 1-58 (lire en ligne, consulté le ).
- (en) V. A. Lubarda, « On the Gibbs conditions of stable equilibrium, convexity and the second-order variations of thermodynamic potentials in nonlinear thermoelasticity », International Journal of Solids and Structures, vol. 45, no 1, , p. 48-63 (DOI 10.1016/j.ijsolstr.2007.07.010, lire en ligne [PDF], consulté le ).
- (en) Santi Prestipino et Paolo V. Giaquinta, « The Concavity of Entropy and Extremum Principles in Thermodynamics », Journal of Statistical Physics, vol. 111, , p. 479–493 (DOI 10.1023/A:1022233814184, lire en ligne, consulté le ).
Bibliographie
- (en) Jean-Philippe Ansermet et Sylvain D. Brechet, Principles of Thermodynamics, Cambridge University Press, , 542 p. (ISBN 9781108426091, lire en ligne), chapitre 6.
- (en) Phil Attard, Thermodynamics and Statistical Mechanics : Equilibrium by Entropy Maximisation, Academic Press, , 424 p. (ISBN 9780120663217, lire en ligne).
- (en) Franco Battaglia et Thomas F. George, Fundamentals in Chemical Physics, Kluwer Academic Publishers, , 315 p. (ISBN 9780792352143, lire en ligne).
- (en) Herbert B. Callen, Thermodynamics and an Introduction to Thermostatistics, New York, John Wiley & Sons, , 2e éd., 512 p. (ISBN 978-0-471-86256-7 et 978-0-471-61056-4, OCLC 11916089, lire en ligne).
- (en) Long-Qing Chen, Thermodynamic Equilibrium and Stability of Materials, Springer Nature, , 464 p. (ISBN 9789811386916, lire en ligne).
- Pierre Infelta et Michael Graetzel, Thermodynamique : Principes et Applications, BrownWalker Press, , 484 p. (ISBN 978-1-58112-995-3, lire en ligne).
- Walter Greiner, Ludwig Neise et Horst Stöcker (trad. de l'anglais par Hans Aksas), Thermodynamique et mécanique statistique [« Thermodynamics and Statistical Mechanics »], New York, Springer, , 532 p. (ISBN 9783540661665, lire en ligne).
- (en) Michel Le Bellac, Fabrice Mortessagne et G. George Batrouni, Equilibrium and Non-Equilibrium Statistical Thermodynamics, Cambridge University Press, , 616 p. (ISBN 9780521821438, lire en ligne).
- (en) Mário J. de Oliveira, Equilibrium Thermodynamics, Springer Science & Business Media, , 382 p. (ISBN 9783642365492, lire en ligne), p. 57-63.
- (en) Luca Peliti, Statistical Mechanics in a Nutshell, vol. 10, Princeton University Press, coll. « In a Nutshell », , 398 p. (ISBN 9780691145297, lire en ligne), chapitre 2.
- Michel Soustelle, Outils de la modélisation des phases : Application aux gaz, vol. 1, Londres, ISTE Group, coll. « Génie des procédés / Thermodynamique chimique approfondie », 2015a, 288 p. (ISBN 9781784050733, lire en ligne).
- (en) Andrew M. Steane, Thermodynamics : A Complete Undergraduate Course, Oxford University Press, , 436 p. (ISBN 9780198788560, lire en ligne), chapitre 17.
- Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique : + de 6500 termes, nombreuses références historiques, des milliers de références bibliographiques, Louvain-la-Neuve, De Boeck Supérieur, , 4e éd. (1re éd. mai 2008), 956 p. (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, SUDOC 224228161, présentation en ligne, lire en ligne).
Liens externes
- Julien Bobroff, Université Paris-Sud, « Thermodynamique classique » [PDF], sur hebergement.u-psud.fr, (consulté le ).
- Olivier Bonnefoy, École des Mines de Saint-Étienne, « Thermodynamique » [PDF], sur emse.fr, (consulté le ).
- Baptiste Bouillot, École des Mines de Saint-Étienne, « Thermodynamique Classique : Approche axiomatique, construction d’un édifice Thermodynamique » [PDF], sur emse.fr, 2016-2017 (consulté le ).
- Marthe Boyomo Onana, École nationale supérieure polytechnique de Yaoundé, École polytechnique fédérale de Lausanne, « Critères de stabilité » [vidéo], sur fr.coursera.org (consulté le ).
- (en) Henri J.F. Jansen, Université de l'Oregon, « Thermodynamics » [PDF], sur sites.science.oregonstate.edu, (consulté le ).
- Hervé Lemonnier, CEA Grenoble, « Thermodynamique et transitions de phase » [PDF], sur herve.lemonnier.sci.free.fr (consulté le ).
- Patrick Puzo, Université Paris-Saclay, « Thermodynamique classique » [PDF], sur hebergement.u-psud.fr (consulté le ), chapitre 5 - Conséquences des deux premiers principes.
- Claude Rozé, Université de Rouen-Normandie, « Thermodynamique : des principes à l'étude de systèmes industriels » [PDF], sur gsi-energie.univ-rouen.fr, (consulté le ).
- École polytechnique fédérale de Zurich, « Convexité, transformée de Legendre et potentiels thermodynamiques » [PDF], sur people.phys.ethz.ch (consulté le ).
- (en) Istituto nazionale di fisica nucleare (INFN), section de Gênes, « Convex Functions and Thermodynamics Potentials » [PDF], sur ge.infn.it (consulté le ).
Articles connexes
- Coefficients calorimétriques et thermoélastiques
- Deuxième principe de la thermodynamique
- Énergie interne
- Entropie (thermodynamique)
- Équilibre chimique
- Équilibre thermique
- Potentiel thermodynamique
- Premier principe de la thermodynamique
- Principe zéro de la thermodynamique
- Thermodynamique














![{\displaystyle \mathrm {d} \left[U+U_{\text{ext}}\right]=\mathrm {d} U+\mathrm {d} U_{\text{ext}}=0}](https://img.franco.wiki/i/6f838d8e2c69143a3dbe95acf4bb74bc0b1cab09.svg)





















![{\displaystyle \mathrm {d} \left[S+S_{\text{ext}}\right]=\mathrm {d} S+\mathrm {d} S_{\text{ext}}\geq 0}](https://img.franco.wiki/i/ecdf31a90971b97bf85e0fd1773ec52a743aa739.svg)



![{\displaystyle \delta W_{P}=-P\,\mathrm {d} \left[V+V_{\text{ext}}\right]=0}](https://img.franco.wiki/i/48f06842cb26012fd1545c11be82f516b199138c.svg)











![{\displaystyle \mathrm {d} U+\mathrm {d} U_{\text{ext}}=\mathrm {d} \left[U+U_{\text{ext}}\right]=\sum _{i}U_{X_{i}}\,\mathrm {d} X_{i}+T\,\left[\mathrm {d} S+\mathrm {d} S_{\text{ext}}\right]=0}](https://img.franco.wiki/i/0e80dc56a627c9bc322ad76d569cdc89d4463226.svg)
![{\displaystyle \mathrm {d} S+\mathrm {d} S_{\text{ext}}=\mathrm {d} \left[S+S_{\text{ext}}\right]\geq 0}](https://img.franco.wiki/i/2282d4150d20119a1f852d23047e651be2cd646b.svg)

![{\displaystyle \mathrm {d} \Phi =\mathrm {d} U+P\,\mathrm {d} V-T\,\mathrm {d} S=\sum _{i}U_{X_{i}}\,\mathrm {d} X_{i}=-T\,\mathrm {d} \left[S+S_{\text{ext}}\right]\leq 0}](https://img.franco.wiki/i/258bfbcf4e3afc12a2db57eec05e89f0bf39ee57.svg)
![{\displaystyle \mathrm {d} S-{\delta Q \over T}=-{1 \over T}\left[\sum _{i}U_{X_{i}}\,\mathrm {d} X_{i}\right]\geq 0}](https://img.franco.wiki/i/c64cfca64ca88bb3e621ea4a837a8ae56ae4cee1.svg)


![{\displaystyle \mathrm {d} \Phi =\mathrm {d} U-T\,\mathrm {d} S=\mathrm {d} \left[U-TS\right]=\mathrm {d} F\leq 0}](https://img.franco.wiki/i/5946ce822fe298e789fe4096a48633d2e1cbccd4.svg)

![{\displaystyle \mathrm {d} \Phi =\mathrm {d} U+P\,\mathrm {d} V=\mathrm {d} \left[U+PV\right]=\mathrm {d} H\leq 0}](https://img.franco.wiki/i/452339edeec791dd7af5afe04c998b938673169b.svg)

![{\displaystyle \mathrm {d} \Phi =\mathrm {d} U+P\,\mathrm {d} V-T\,\mathrm {d} S=\mathrm {d} \left[U+PV-TS\right]=\mathrm {d} G\leq 0}](https://img.franco.wiki/i/a9b87eca2b8e3b6e4b406842e7f5d8396157cf4e.svg)














![{\displaystyle \left[1-\tau \right]\beta }](https://img.franco.wiki/i/58eb0fc285881a2556edfa48bc45b951795630dd.svg)

![{\displaystyle V^{\left[1-\tau \right]\beta }=\left[1-\tau \right]\,V^{\beta },\,U^{\left[1-\tau \right]\beta }=\left[1-\tau \right]\,U^{\beta },\,X_{1}^{\left[1-\tau \right]\beta }=\left[1-\tau \right]\,X_{1}^{\beta },\,X_{2}^{\left[1-\tau \right]\beta }=\left[1-\tau \right]\,X_{2}^{\beta },\cdots }](https://img.franco.wiki/i/7742cc0d2b44d9383bfd912ee71653ecb2be62a0.svg)

![{\displaystyle S^{\left[1-\tau \right]\beta }=S\!\left(\left[1-\tau \right]\,V^{\beta },\left[1-\tau \right]\,U^{\beta },\left[1-\tau \right]\,X_{1}^{\beta },\left[1-\tau \right]\,X_{2}^{\beta },\cdots \right)=\left[1-\tau \right]\,S\!\left(V^{\beta },U^{\beta },X_{1}^{\beta },X_{2}^{\beta },\cdots \right)=\left[1-\tau \right]\,S^{\beta }}](https://img.franco.wiki/i/99c3492d996799c48a47d134c44535149cb9b544.svg)
![{\displaystyle \tau \alpha +\left[1-\tau \right]\beta }](https://img.franco.wiki/i/3510ff0fb1456310178c84013f46318c8ffef1e8.svg)
![{\displaystyle \tau \,U^{\alpha }+\left[1-\tau \right]\,U^{\beta }}](https://img.franco.wiki/i/62424f7f0fbc9f7861653a0e114f765eeb113426.svg)
![{\displaystyle V^{\tau \alpha +\left[1-\tau \right]\beta }=\tau \,V^{\alpha }+\left[1-\tau \right]\,V^{\beta },\,U^{\tau \alpha +\left[1-\tau \right]\beta }=\tau \,U^{\alpha }+\left[1-\tau \right]\,U^{\beta },\,X_{1}^{\tau \alpha +\left[1-\tau \right]\beta }=\tau \,X_{1}^{\alpha }+\left[1-\tau \right]\,X_{1}^{\beta },\,X_{2}^{\tau \alpha +\left[1-\tau \right]\beta }=\tau \,X_{2}^{\alpha }+\left[1-\tau \right]\,X_{2}^{\beta },\cdots }](https://img.franco.wiki/i/d1a481841b424d3193076acbf5a3e8c76bd8209e.svg)
![{\displaystyle S^{\tau \alpha +\left[1-\tau \right]\beta }=S\!\left(\tau \,V^{\alpha }+\left[1-\tau \right]\,V^{\beta },\tau \,U^{\alpha }+\left[1-\tau \right]\,U^{\beta },\tau \,X_{1}^{\alpha }+\left[1-\tau \right]\,X_{1}^{\beta },\tau \,X_{2}^{\alpha }+\left[1-\tau \right]\,X_{2}^{\beta },\cdots \right)}](https://img.franco.wiki/i/713d8cc7796ba248dfbbfb712da944d76b4fd39d.svg)
![{\displaystyle \tau \,S^{\alpha }+\left[1-\tau \right]\,S^{\beta }}](https://img.franco.wiki/i/e81527bc3229d6d14c920c3969e1c3466254c057.svg)
![{\displaystyle S^{\tau \alpha +\left[1-\tau \right]\beta }\geq \tau \,S^{\alpha }+\left[1-\tau \right]\,S^{\beta }}](https://img.franco.wiki/i/be69e3d917641cfd50f00721514d48a147e03212.svg)
































![{\displaystyle \mathrm {d} \left[S+S_{\text{ext}}\right]\geq 0}](https://img.franco.wiki/i/6755ddac0e5c5561a51c223d9fff27c4d6bec991.svg)
![{\displaystyle \mathrm {d} \left[U+U_{\text{ext}}\right]=0}](https://img.franco.wiki/i/d8feb4ea100eff651b173a820e45bcc70f76521b.svg)
![{\displaystyle \mathrm {d} \left[S+S_{\text{ext}}\right]=0}](https://img.franco.wiki/i/523dec6dc768f9649e9049e313cd53fe19e4226b.svg)
![{\displaystyle \mathrm {d} ^{2}\left[S+S_{\text{ext}}\right]\leq 0}](https://img.franco.wiki/i/f8f5f6a0a8c1e0fedf8982a82c77630e5d23324c.svg)
![{\displaystyle \mathrm {d} ^{2}\left[U+U_{\text{ext}}\right]\geq 0}](https://img.franco.wiki/i/ebae2240dfaf21ab1d36fec69add814bcfe55df8.svg)





![{\displaystyle \mathrm {d} \Phi =\mathrm {d} F=\sum _{i}U_{X_{i}}\,\mathrm {d} X_{i}=-T\,\mathrm {d} \left[S+S_{\text{ext}}\right]\leq 0}](https://img.franco.wiki/i/d2d9fc12e3584fffec02163d034b9b07418d673b.svg)












![{\displaystyle \mathrm {d} \Phi =\mathrm {d} G=\sum _{i}U_{X_{i}}\,\mathrm {d} X_{i}=-T\,\mathrm {d} \left[S+S_{\text{ext}}\right]\leq 0}](https://img.franco.wiki/i/d86e4f1d99c266f99ce65781f15202b955ba5558.svg)






















































































































![{\displaystyle i\in [1,\cdots ,N]}](https://img.franco.wiki/i/b408c2723c4b77edc723df1fdc3eab75284902b9.svg)

































































































![{\displaystyle \delta Q_{P}=\mathrm {d} U+P\,\mathrm {d} V=\mathrm {d} \left[U+PV\right]=\mathrm {d} H}](https://img.franco.wiki/i/cd9accade39bedbe35dc1f15c7995d18ff660670.svg)

![{\displaystyle \mathrm {d} ^{2}S=\mathrm {d} {1 \over T}\,\mathrm {d} U+\mathrm {d} {P \over T}\,\mathrm {d} V=\mathrm {d} {1 \over T}\,\mathrm {d} \left[U+PV\right]=\mathrm {d} {1 \over T}\,\mathrm {d} H=-{1 \over T^{2}}\,\mathrm {d} T\,\mathrm {d} H}](https://img.franco.wiki/i/a91ae8a49a50375e6e6f3bc97f5611998199af2d.svg)







































































![{\displaystyle \left[Y\neq X\right]}](https://img.franco.wiki/i/d411bf9c55132f5d2ba85e81b040fb1e3e39dfe8.svg)
![{\displaystyle \left[Y\neq \xi \right]}](https://img.franco.wiki/i/b1c7e88fb7c111cad65bcc3bca5fa09e2ab3c3ea.svg)
![{\displaystyle \left[Y\neq X\right]\cap \left[Y\neq \xi \right]}](https://img.franco.wiki/i/8e08a62f795e4b0761c3d07888a34d45e90ee273.svg)













































![{\displaystyle \mathrm {d} \Phi =\mathrm {d} U+P\,\mathrm {d} V-T\,\mathrm {d} S=\gamma \,\mathrm {d} A=-T\,\mathrm {d} \left[S+S_{\text{ext}}\right]\leq 0}](https://img.franco.wiki/i/b68a46401fcde6f86d2ac8f5ce864633fafd8721.svg)










![{\displaystyle \mathrm {d} U=\sum _{k=1}^{K}\left[-P\,\mathrm {d} V^{k}+\gamma \,\mathrm {d} A^{k}+T\,\mathrm {d} S^{k}+\sum _{i=1}^{N}\mu _{i}\,\mathrm {d} n_{i}^{k}\right]}](https://img.franco.wiki/i/f75b190ee58132b936f27797ed05fd2608085231.svg)




![{\displaystyle \mathrm {d} \Phi =\mathrm {d} G=\gamma \,\mathrm {d} A=-T\,\mathrm {d} \left[S+S_{\text{ext}}\right]\leq 0}](https://img.franco.wiki/i/5b6a8f42517dcf4bc73a8671bbf922b2b67d1f43.svg)



















![{\displaystyle {\begin{aligned}\mathrm {d} ^{k}\Phi (X^{\circ },\mathrm {d} X)&=\sum _{i_{1}=1}^{n}\sum _{i_{2}=1}^{n}\cdots \sum _{i_{k}=1}^{n}\left({\partial ^{k}\Phi \over \partial X_{i_{1}}\partial X_{i_{2}}\cdots \partial X_{i_{k}}}\right)\!\left(X^{\circ }\right)\,\mathrm {d} X_{i_{1}}\,\mathrm {d} X_{i_{2}}\,\cdots \,\mathrm {d} X_{i_{k}}\\&=\left[\sum _{i=1}^{n}\left({\partial \,\cdot \over \partial X_{i}}\right)\!\left(X^{\circ }\right)\,\mathrm {d} X_{i}\right]^{k}\Phi \end{aligned}}}](https://img.franco.wiki/i/8215e42ab32e23da47b2d3f9490f7f4a7a6e5b51.svg)

















































































































































































