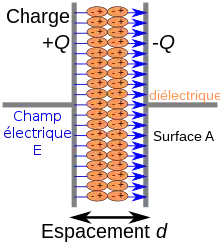
Un milieu est diélectrique (mot composé du préfixe grec δια- / dia- (« au travers ») et électrique[1]) s'il ne contient pas de charges électriques susceptibles de se déplacer de façon macroscopique. Le milieu ne peut donc pas conduire le courant électrique, et est souvent un isolant électrique. Les milieux diélectriques incluent par exemple le vide, le verre, le bois sec, l'eau pure et de nombreux plastiques.
Les diélectriques ne sont cependant pas inertes électriquement. En effet, les constituants du matériau peuvent présenter à l'échelle atomique des dipôles électrostatiques, qui interagiront avec un champ électrique externe appliqué. Cette interaction se traduit par la création d'une polarisation reliée au niveau microscopique à ce champ électrique par la polarisabilité, et au niveau macroscopique, par la susceptibilité électrique .
Définitions et grandeurs caractéristiques
Les matériaux diélectriques sont caractérisés en particulier par[2] :
- leur permittivité diélectrique ε, ou constante diélectrique ;
- leur rigidité diélectrique ;
- leur angle de perte ou tangente delta, tan(δ).
Définitions
Les mots isolant et diélectrique tendent à être utilisés comme des synonymes[3]. Un isolant est un matériaux dont la conductivité électrique est faible. La borne maximale est relativement arbitraire. Un diélectrique se caractérise par l'apparition d'une polarisation lorsque le matériaux est soumis à un champ[4].
Tout matériau présente, au moins, une polarisabilité électronique, puisqu'elle existe pour tout type d'atome. Ainsi, tout matériau isolant est diélectrique. En toute rigueur, seul le vide est un isolant non-diélectrique (et même cela est discutable car il existe une polarisation du vide), néanmoins les propriétés diélectriques d'un gaz sous faible pression sont souvent négligeables. L'usage des termes « isolant » ou « diélectrique » dépend essentiellement du contexte, de l'application visée : on parle d'isolant quand on s'intéresse à la capacité du matériaux à bloquer le courant, de diélectrique quand on s'intéresse à sa capacité à se polariser[5]. Le terme « diélectrique » a été créé par William Whewell, il apparait pour la première dans sa correspondance avec Michael Faraday[6].
Certaines propriétés diélectriques sont cependant définies pour des matériaux qui ne sont pas isolants. On peut ainsi généraliser la permittivité aux semi-conducteurs[3] et aux métaux : on parle alors de fonction diélectrique complexe car la permittivité est alors un nombre complexe qui dépend de la fréquence. Sa partie réelle est alors associée aux processus diélectriques usuels (polarisation) alors que sa partie imaginaire est associée au phénomènes dissipatifs.
Les matériaux piézoélectriques sont un sous-ensemble des diélectriques solides cristallins, chez lesquels il existe une relation entre champ électrique et déformation mécanique.
Permittivité et susceptibilité
La permittivité se définit comme le rapport entre le vecteur déplacement (ou induction) électrique, dans un milieu donné et le champ électrique. C'est une grandeur macroscopique d'un milieu, issue de son comportement global, et qui n'a plus de sens à l'échelle moléculaire[7].
La permittivité est un simple scalaire dans un matériau isotrope. Néanmoins, dans les matériaux anisotrope, elle prend la forme d'un tenseur sous la forme d'une matrice (3,3), et le vecteur de déplacement n'est alors pas nécessairement colinéaire au vecteur champ électrique[8] :
La permittivité se mesure en farads par mètre. On utilise souvent la permittivité relative, ou constante diélectrique du matériau, c'est-à-dire normée par rapport à celle du vide, qui vaut 8,854 × 10−12 F/m[9] :
Le vecteur polarisation est l'incrément de par rapport à sa valeur dans le vide :
La susceptibilité vaut donc (ou moins la matrice identité dans le cas non-isotrope).
Évaluation des pertes en régime alternatif
En régime alternatif, la permittivité est complexe. Une convention souvent utilisée (mais pas toujours) est de noter sa partie réelle et, la partie imaginaire étant négative, son opposé[10].
La partie imaginaire de la permittivité exprime une dissipation d'énergie. Dans le cas d'une capacité plane de surface et d'entrefer , elle se traduit par une partie réelle positive de l'impédance :
L'angle de perte (adimensionnel) est une façon usuelle de formuler l'importance de la dissipation d'énergie :
Les pertes sont un critère majeur des performances d'un diélectrique pour les applications en haute fréquence. On cherche à utiliser le diélectrique présentant les pertes le plus faibles possible dans la gamme de fréquence de l'application[10]. L'inverse du est appelé facteur de qualité et noté [11].
Mécanismes de polarisation
Les électrons présents dans un milieu diélectrique ne peuvent pas, par définition, se déplacer sur des grandes distances. Ils peuvent par contre présenter des mouvements d'amplitude très petite à notre échelle, mais qui peuvent être à l'origine de nombreux phénomènes. Ces mouvements sont souvent des mouvements d'oscillation autour du noyau : le nuage électronique peut être déformé et ainsi créer un dipôle électrostatique. Il en va de même pour le déplacement global des noyaux ioniques au sein du matériau (ils créent également des dipôles). Le troisième mécanisme présent est la réorientation, sous l'effet du champ appliqué, de dipôle existants (comme les molécules d'eau).
Cette polarisation provient trois effets physiques différents. Ils sont représentés ici, chacun étant très exagéré :
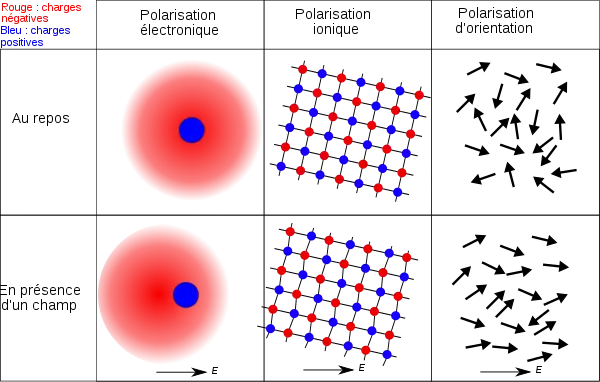
Un quatrième mécanisme, la polarisation d'interface, existe dans les matériaux granulaires.
Polarisation électronique
La polarisation électronique, présente dans toute matière, est due au déplacement et à la déformation de chaque nuage électronique : sous l'influence du champ, le nuage est décentré par rapport au noyau de l'atome. Ainsi le barycentre des charges négatives n'est plus confondu avec celui des charges positives, et chaque atome présente un dipôle. La composante de premier ordre de la polarisation due à ce phénomène se calcule en déterminant le déplacement du nuage électronique, calcul qui est assez simple à condition de poser des hypothèses fortes[12].
Un modèle simple consiste à représenter les électrons comme étant reliés au noyau par une raideur . Il permet de déterminer le moment créé par le nuage électronique d'un atome[13].
Polarisation ionique
La polarisation ionique (ou atomique) est due aux déplacements des atomes, par déformation de la structure. L'exemple illustré ci-dessus correspond à un cristal ionique très simple où les anions et les cations sont alternés (chlorure de sodium par exemple)[14].
Polarisation d'orientation
La polarisation d'orientation existe lorsque des dipôles sont déjà présents. En l'absence de champ appliqué leur orientation est aléatoire, leur somme est donc nulle. Le champ tend à les aligner, créant une densité moyenne de moment dipolaire non nulle. C'est le mécanisme dominant dans les liquides, lorsque chaque molécule présente un moment électrique, ce qui caractérise un liquide polaire. Il est responsable de leur permittivité relative très élevée, par exemple près de 80 pour l'eau. Cet effet présente une saturation (non-linéarité) : lorsque le champ appliqué est très important, les dipôles finissent par être tous parfaitement alignés, et la polarisation ne peut être accrue. En outre, il présente une limite en fréquence, les molécules ne pouvant suivre un champ trop rapide[15].
La polarisation est souvent proportionnelle au champ électrique qui est le champ électrique total après que la matière a été polarisée (ce cas est dit linéaire) :
- ,
avec la permittivité du vide et la susceptibilité électrique du matériau, qui est un nombre complexe. Dans le cas d'un diélectrique anisotrope, est un tenseur de rang 2.
En généralisant cela à des phénomènes où la polarisation n'est pas proportionnelle au champ électrique, on atteint le domaine de l'optique non linéaire.
Définition de la polarisabilité
En considérant une molécule isolée, sa polarisabilité se définit comme le rapport entre le champ électrique local et le moment dipôlaire crée par la polarisation électronique : . Cette expression donne, selon le milieu étudié, des résultats différents[16] :
- si la densité du milieu est très faible, et si aucun autre mécanisme de polarisation n'intervient (par exemple un gaz à faible pression, formé de molécules apolaires) . On a alors une relation directe entre et : , où est le nombre de molécule par unité de volume ;
- dans un milieu plus dense, l'influence des molécules sur le champ n'est plus négligeable. Cela crée une sorte de rétroaction qui conduit à ;
- dans un milieu dense à molécules polaires, le moment dipolaire permanent des molécules s'y ajoute : . On fait ici intervenir la constante de Boltzmann k et la température T.
Polarisation d'interface
Ce quatrième mécanisme de polarisation n'intervient que dans les diélectriques hétérogènes[17].
Phénomènes d'intérêt dans les diélectriques
Relaxation diélectrique
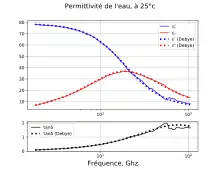
La formation (ou la disparition) d'une polarisation n'est pas instantanée. Elle a un temps de réaction, ce qui cause un retard, la relaxation diélectrique. La conséquence est que les propriétés diélectriques varient avec la fréquence[19].
Chacun des mécanismes de polarisation a une limite en fréquence et est donc associée à une relaxation diélectrique, mais les ordres de grandeurs des fréquences concernées sont très différents[20] :
- pour la polarisation d'interface, les fréquences sont basses, de l'ordre de la centaine de kHz ;
- pour la polarisation d'orientation, la relaxation se produit dans des fréquences de l'ordre du GHz ;
- pour la polarisation ionique, l'ordre de grandeur est celui du THz (1012 Hz) ;
- enfin, pour la polarisation atomique, le phénomène se produit au-delà de 1014 Hz, dans le domaine optique.
Le modèle de relaxation diélectrique le plus simple est celui de Peter Debye, qui tient compte de la polarisation comme d'un simple phénomène d'ordre un, de constante de temps . Pour une polarisation d'orientation, cela revient à supposer qu'il n'y a qu'un type de dipôles, et qu'ils n’interagissent pas entre eux[19]. La constante diélectrique prend alors la forme complexe suivante :
étant la fréquence angulaire. Dans cette écriture, est la permittivité à l'infini (en très haute fréquence), elle est réelle et correspond à la situation où les dipôles ne sont plus du tout mobiles. est la permittivité statique, c'est-à-dire observée en très basse fréquence, lorsque les dipôles réagissent en régime forcé. Dans la zone de transition, la partie imaginaire de la permittivité devient importante, traduisant des pertes : de l'énergie est perdue à déplacer les dipôles.
Développée dans le cas des liquides, l'équation de Debye est rarement suffisante pour décrire le comportement des solides. Il existe différents modèles plus détaillés, qui tous en dérivent et l'admettent comme cas particulier[19] :
- l'équation de Cole-Cole introduit un facteur , qui permet d'aplatir la réponse en fréquence :
- l'équation de Davidson-Cole asymétrise la réponse en fréquence :
- l'équation de Havriliak-Negami se présente comme une combinaison des précédentes :
Si la relaxation diélectrique existe pour tous les mécanismes de polarisation, elle est particulièrement importante pour la polarisation par orientation, donc le temps de relaxation est le plus long. Ainsi dans l'exemple de l'eau, la polarisation par relaxation a un temps de relaxation de 9,3 ps. La loi de Debye calculée pour cette relaxation donne un maximum de pertes à 17 GHz, et elle prédit parfaitement la permittivité de l'eau jusqu'à environ 100 GHz — à ces fréquences seulement, les autres phénomènes interviennent[21].
Dans un matériau donné, dépend, à la baisse, de la température : en effet l'agitation thermique facilite la réorientation du dipôle[19].
Phénomènes de réfraction, de réflexion et d'absorption

La polarisation créée dans le milieu diélectrique intervient dans des phénomènes mettant en jeu des ondes électromagnétiques, comme la lumière, car elles présentent un champ électrique. Les équations de Maxwell permettent alors de montrer que la partie réelle de modifie la vitesse c d'une onde lumineuse se propageant dans le matériau par rapport à la vitesse c0 qu'elle aurait dans le vide selon la relation suivante, valable dans les matériaux magnétiquement inertes (c'est-à-dire dont la perméabilité magnétique reste égale à celle du vide)[22] :
- .
Cela correspond exactement à la définition de l'indice de réfraction n d'un milieu : . Cela explique donc le phénomène de réfraction de la lumière. D'autre part, la partie imaginaire correspond à une absorption de la lumière par le matériau. Lorsque le matériau est anisotrope, les relations ne sont pas aussi simples, et on voit apparaître le phénomène de biréfringence : deux rayons sont réfractés au lieu d'un seul[23].
La réflexion peut également être comprise de cette façon. On peut alors montrer que, au passage de la lumière à travers un dioptre séparant deux milieux différents, une partie de l'onde est réfléchie, et le reste est réfracté. Le calcul correspondant aboutit aux coefficients de Fresnel qui donnent les proportions de la lumière réfléchie et réfractée. Dans le cas où toute la lumière est réfléchie (réflexion totale), on peut observer une onde évanescente, c'est-à-dire une onde de très courte portée qui apparaît de l'autre côté du dioptre. On peut même, en plaçant un autre dioptre très proche du premier, récupérer cette onde évanescente : c'est le phénomène de réflexion totale frustrée[24].
Claquage diélectrique
Le claquage diélectrique est le phénomène par lequel un diélectrique, soumis à un champ électrique trop important — dépassant une valeur appelée la « rigidité diélectrique » du matériau —, devient conducteur (provoquant un arc électrique). Les mécanismes sous-jacents sont assez différents dans le cas d'un fluide ou d'un solide.
Dans un gaz
Dans un gaz, la rigidité diélectrique dépend de la pression, passant par un minimum (loi de Paschen). Plusieurs mécanismes de claquage existent. À pression ambiante (et de façon plus générale, au-dessus du minimum de Paschen), le mécanisme usuel est la décharge impulsionnelle. Les ions qui existent naturellement dans un gaz sont accélérés par le champ électrique, et, par collision avec les molécules neutres, peuvent produire de nouveaux ions. Passé un champ électrique suffisant, ceci devient une réaction en chaîne, le gaz devient conducteur. Le processus de Townsend, plus important à basse pression, répond à une logique similaire, mais concerne les électrons libres présents dans le gaz, qui arrachent d'autres électrons par collision avec les molécules. Dans le vide ou dans un gaz à très faible pression, un troisième mécanisme se manifeste : le claquage du vide se produit lorsque la distance entre les électrodes devient inférieure au temps de vol libre moyen d'un électron, leur permettant de « sauter » de la cathode à l'anode[25]. La lampe à décharge est une application usuelle du claquage diélectrique des gaz[26].
Dans un liquide
Dans un liquide, plusieurs mécanismes de claquages diélectriques peuvent exister. On distingue :
- des phénomènes électroniques, très rapides (sous la microseconde). Il s'agit de la libération d'électrons par avalanche, comme dans les gaz[27] ;
- des phénomènes thermiques, d'une durée supérieure à la microseconde, qui se manifestent par la formation de bulles. Si le liquide est très pur, en l'absence de sites de nucléation, il peut passer dans un état de surchauffe, c'est-à-dire dépasser son point d'ébullition tout en restant liquide, une ébullition très brutale se produit alors quand la température critique est atteinte. En revanche, si des impuretés sont présentes, elles jouent le rôle de site de nucléations et le phénomène est plus progressif[28].
L'intérêt de l'étude du claquage des liquides est double. D'un côté, il s'agit de l'éviter pour les liquides utilisés comme isolants, notamment dans les transformateurs. De l'autre, le claquage intentionnel des liquides est utilisé, notamment comme source acoustique pour les sonars et la prospection pétrolière[27],[28].
Dans un solide

Dans un solide, le claquage diélectrique est destructif : le diélectrique perd définitivement ses propriétés. Ici encore, il existe plusieurs mécanismes. Les mécanismes les plus rapides nécessitent les champs les plus élevés. Une fois que le claquage a eu lieu, le champ électrique s'effondre et les mécanismes plus lents n'ont plus l'occasion de se produire[29] :
- le claquage intrinsèque est celui qui nécessite le champ le plus élevé, et le plus rapide. Des électrons présents dans la bande de conduction, accélérés par le champ, entrent en collision avec les atomes du matériau, et libèrent de nouveaux électrons. La durée de vie des électrons de conduction est limitée, le phénomène devenant exponentiel quand le nombre d'électrons engendrés est supérieur au nombre d'électrons qui retombent dans la bande de valence ;
- le claquage par avalanche est dû à la génération d'électrons par collision, à partir d'un électron libre injecté à la cathode. Il est dépendant de la géométrie (se manifestant à partir des pointes) ;
- le claquage thermique est dû à la fuite de courant à travers le diélectrique. Sa conductivité n'étant pas nulle, un faible courant le traverse, provoquant un échauffement ohmique. S'il devient trop important pour la dissipation de chaleur possible, le phénomène devient destructif. Ce type de claquage est donc relativement lent, l'inertie thermique du matériau empêchant une élévation instantanée de la température ;
- le claquage électrochimique est un phénomène assez lent, dû à une dégradation chimique d'un matériau constamment soumis à un champ électrique par des réactions chimiques avec le milieu ambiant (air, humidité…).
Piézoélectricité et phénomènes associés
Les matériaux piézoélectriques sont une famille de diélectriques solides. Ce sont des cristaux ioniques (alternance d'anions et de cations) présentant une structure cristalline non centrosymétrique, c'est-à-dire qu'il y a une asymétrie dans le répartition des raideurs mécaniques entre les ions. Pour ces matériaux, la polarisation ionique est associée à une déformation élastique. Ainsi, en comprimant ou en étirant le matériau, on crée un champ électrique en son sein, réciproquement, il se déforme lorsqu'il est soumis à un champ électrique. Vingt classes cristallines pésentent des propriétés piézoélectriques. Ces matériaux sont fondamentalement anisotropes : ils ont un axe privilégié, un champ appliqué sur cet axe tend à dilater ou à comprimer le matériaux selon la direction[30].
Les pyroélectriques sont un sous-ensemble des piézoélectriques : dix des vingt classes piézoélectriques sont aussi pyroélectriques. L'effet pyroélectrique est une modification de la polarisation spontanée du matériau sous l'effet d'un changement de température. Enfin les ferrélectriques sont une classe de pyroélectriques qui peuvent être repolarisés : en appliquant un champ électrique suffisant, on peut modifier, ou même inverser, leur polarisation, et ce changement perdure après le retour à un champ nul[16].
Électrophorèse, diélectrophorèse et électrorotation
Ces trois phénomènes concernent des particules en suspension dans un liquide diélectrique, en présence d'un champ électrique[31] :
- l'électrophorèse concerne les particules chargées, elles sont attirées dans la direction du champ, ou dans la direction opposé selon le signe de leur charge ;
- l'électrorotation concerne une particule neutre, mais polarisée, elle tourne grâce au moment que le champ applique sur elle ;
- la diélectrophorèse concerne aussi une particule neutre polarisée, qui est attirée par le gradient de l'amplitude du champ.
Diélectriques solides
Les diélectriques étant de bons isolants électriques et thermiques, et sont donc utilisés pour gainer les câbles électriques afin d'éviter des contacts avec d'autres câbles ou des personnes.
Les diélectriques sont utiles dans les condensateurs. Dans le cas, très simple, du condensateur plan, on peut rapprocher les plaques sans risque de contact ou de claquage. On insère ainsi des couches de diélectriques dans les condensateurs industriels, ce qui permet d'augmenter la capacité en diminuant l'encombrement.
D'autre part, si on la soumet à un champ électrique suffisamment puissant, toute substance s'ionisera et deviendra conductrice. Les diélectriques étant plutôt difficiles à ioniser, l'air ambiant devient conducteur avant eux : on peut les employer pour des condensateurs à haute tension.
La plupart des diélectriques sont également transparents dans de larges gammes de fréquences, et sont parfois utilisés en optique pour constituer une couche anti-reflet, par exemple sur certains modèles de verres de lunette.
Haute tension et électrotechnique

Dans le domaine de la haute tension et en électrotechnique :
- le verre, utilisé pour faire des isolateurs de lignes haute tension[2] ;
- la céramique, très utilisée pour les matériels HTB des postes électriques[2] ;
- la plupart des plastiques, en particulier polyéthylène sous sa forme réticulée (XLPE) et PVC, tous deux utilisés pour les câbles[2] ;
- le polypropylène, utilisé en particulier dans les condensateurs en HTA ou HTB[2] ;
- le mica, qui n'est guère plus utilisé de nos jours dans l'industrie électrotechnique ;
- le Téflon, utilisé pour certaines pièces des disjoncteurs à haute tension[2] ;
- le papier imprégné d'huile minérale sert à former l'isolation des transformateurs[2] ;
- la résine époxyde est utilisée dans les traversées électriques.
Composants discrets et cartes électroniques
.jpg.webp)
Pour la production de circuits imprimés et de façon plus générale l'appareillage électrique, la Bakélite fut autrefois très utilisée. Elle a assez largement été supplantée par la résine époxyde et les composites l'utilisant, comme le FR-4[32]. Les condensateurs discrets sont de type électrolytique pour les très grandes valeurs, les autres utilisent des diélectriques. On trouve ici plusieurs familles de diélectriques, selon les applications visées[33] :
- différents polymères peuvent être utilisés comme diélectrique : polyéthylène, polypropylène, polymère à base de benzocyclobutène (BCB), polyépoxyde, Mylar, polycarbonate, etc. Ces plastiques ont une permittivité relative modeste, en général entre 2,5 et 4, ce qui limite la valeur des capacités réalisables dans un volume donné. Ils ont d'excellentes propriétés en fréquence : faible pertes, faible effet batterie ;
- des céramiques paraélectriques sont utilisées : oxyde de silicium, nitrure de silicium, alumine, nitrure d'aluminium. Leur permittivité est un peu plus élevée. Elles peuvent former des capacités plus importantes et tenir des tensions plus élevées, mais ont de moins bonnes caractéristiques en fréquence ;
- des matériaux ferroélectriques en couche épaisse permettent de réaliser des capacités de plus grandes valeurs. Ces capacités ont un mauvais comportement en fréquence et sont plutôt adaptés au stockage d'énergie ;
- certains condensateurs utilisent un film polymère chargée de poudre ferroélectrique pour augmenter la permittivité[34] ;
- le papier imprégné d'huile fut largement utilisé, mais est considéré comme obsolète[35].
Microélectronique
La microélectronique CMOS utilise plusieurs diélectriques. L'oxyde de silicium SiO2 est le plus facile à produire dans une filière silicium, et a été le premier utilisé et reste le plus courant. Des diélectriques à plus haute permittivité ont ensuite été utilisés, comme l'alumine, l'oxyde de tantale et l'oxyde de titane[36].
À l'inverse, selon les applications, il peut être souhaitable d'avoir des diélectriques à faible permittivité. Pour cela, sont apparues des silices dopées fluor, avec un de l'ordre de 3,5 au lieu de 3,9[37], des polymères utilisés comme diélectriques[38] et des diélectriques poreux[37]
La filière III-V et notamment arséniure de gallium est pénalisée par le fait de ne pas disposer de diélectriques faciles à intégrer dans ses composants (comme pour réaliser des MOSFET), comme l'est le SiO2 pour la filière silicium. Une des solutions est le dépôt de couche atomique d'alumine[39].
Diélectriques fluides
Liquides
Dans les liquides :
- l'huile minérale, utilisée dans les transformateurs[2] ;
- l'huile de silicone[2] ;
- l'huile végétale, innovation récente dans l'isolation diélectrique dans les transformateurs électriques[2] ;
- le pyralène (PCB), autrefois utilisé dans les transformateurs, mais depuis interdit dans la plupart des pays à cause de sa toxicité[2] ;
- l'eau pure. Si l'eau est habituellement conductrice, une eau parfaitement pure est un très bon isolant. La difficulté de garder dans la durée une eau très pure rend toute utilisation industrielle difficile[2] ;
- l'azote liquide, l'hélium liquide ou le SF6 permettent d'isoler des composants supraconducteurs à très basse température[2].
Gazeux
Caractérisation des propriétés diélectriques
Différentes techniques sont utilisées pour mesurer les propriétés d'intérêt d'un matériaux diélectrique pour l'électrique et la microélectronique, comme la permittivité, le facteur de perte, la rigidité diélectrique, la conductivité électrique, chacun de ces paramètres pouvant être évalué dans des gammes de fréquences variées, et pouvant éventuellement être dépendant de la température, des dimensions de l'échantillon, de la qualité du matériaux, etc.[40],[41].
Essais diélectriques

Les essais diélectriques visent à déterminer les qualités d'un isolant et sa tension de claquage, en le soumettant à des champs très importants. Ils font l'objet d'un cadre normatif pour la sécurité du matériel haute tension[42].
Sonde coaxiale ouverte

Cette méthode utilise un guide d'ondes coaxial qui se termine en s'ouvrant sur le milieu à tester. Un analyseur de réseau permet alors de mesurer le taux de réflexion de l'onde. On peut en déduire l'Impédance caractéristique du milieu étudié, et en déduire, notamment, la permittivité (y compris sa partie imaginaire). Cette méthode, simple et non-destructive, est largement utilisée et concerne une vaste gamme de fréquence, de 0,5 à 100 GHz environ[41].
Mesure en transmission
Comme dans la méthode précédente, on fait usage d'un analyseur de réseau. Ici la mesure se fait en transmission : l'échantillon étudié est placé sur le chemin du guide d'ondes mesuré. C'est souvent une addition à la mesure précédence, car le coefficient de réflexion peut être mesuré simultanément[41].
Mesure à l'air libre
Cette technique repose sur le même principe que la précédence, mais aucun guide d'ondes n'est utilisé. On forme un quadripôle en plaçant deux antennes cornet en regard. Le matériau à caractériser (sous forme d'un panneau) est inteposé entre les deux antennes. La mesure des coefficients de transmission et de réflexion permet de caractériser le matériau dans les radiofréquences[41].
Mesure par cavité résonante
Cette méthode de mesure consiste à réaliser une cavité résonnante dans laquelle est placée l'échantillon à caractériser. La modification de la fréquence de résonance et du facteur de qualité de la cavité (par rapport à son comportement à vide), mesurée à l'aide d'un analyseur de réseau, donne accès à la permittivité complexe de l'échantillon. Cette méthode permet d'obtenir une mesure à une fréquence précise (liée à la cavité), de l'ordre de plusieurs GHz[41],[43].
Mesure de capacité plane
Cette technique fait appel à la définition d'une capacité plane : . Une capacité à électrodes parallèles est fabriquée en utilisant le matériau à caractériser. Les dimensions (surface et épaisseur ) étant connues, une mesure de l'impédance électrique permet de déterminer la permittivité (y compris sa composante imaginaire, c'est-à-dire les pertes). Cette méthode est utile dans des fréquences plus basses que les précédentes, jusqu'au GHz environ[41].
Mesures de vieillissement
En biologie et en médecine
En histologie, la caractérisation des propriétés diélectriques des tissus revait une grande importance : elle est nécessaire pour maitriser les techniques médicales faisant appel aux ondes électromagnétiques, comme l'ablation par radiofréquence, c'est aussi un outil de diagnostic. La méthode de mesure in vivo la plus courante fait appel à une sonde coaxiale appliquée sur la peau. La mesure du coefficient de réflexion en bout de sonde permet d'évaluer la permittivité diélectrique des tissus biologiques[44],[45].
En géophysique

La mesure des propriétés diélectrique du sous-sol se fait par des radars spécialisés, les radars à pénétration de sol. Cette technique permet par exemple de déceler, dans le sous-sol, la présence d'eau sous forme liquide, de neige ou de glace[46], d'assister la prospection archéologique[47] ou de quantifier la pollution par des hydrocarbures[48].
Notes et références
- ↑ Informations lexicographiques et étymologiques de « diélectrique » dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales, consulté le 19 août 2016.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Kuechler 2005, p. 266-306.
- 1 2 « Diélectriques », sur Encyclopædia Universalis (consulté le ).
- ↑ Dang, Zhi-Min, Dielectric polymer materials for high-density energy storage (ISBN 978-0-12-813216-6 et 0-12-813216-7, OCLC 1041143199, lire en ligne).
- ↑ Grécias, Pierre, Physique sup, MPSI & PTSI, Éd. Tec & doc, (ISBN 2-7430-0303-0 et 978-2-7430-0303-6, OCLC 42383341, lire en ligne).
- ↑ David Gooding, « Final Steps to the Field Theory: Faraday's Study of Magnetic Phenomena, 1845-1850 », Historical Studies in the Physical Sciences, vol. 11, no 2, , p. 231–275 (ISSN 0073-2672, DOI 10.2307/27757480, lire en ligne, consulté le )
- ↑ (en) V. Ballenegger et J.-P. Hansen, « Dielectric permittivity profiles of confined polar fluids », The Journal of Chemical Physics, vol. 122, no 11, , p. 114711 (ISSN 0021-9606 et 1089-7690, DOI 10.1063/1.1845431, lire en ligne, consulté le ).
- ↑ (en) D. R. Smith et D. Schurig, « Electromagnetic Wave Propagation in Media with Indefinite Permittivity and Permeability Tensors », Physical Review Letters, vol. 90, no 7, , p. 077405 (ISSN 0031-9007 et 1079-7114, DOI 10.1103/PhysRevLett.90.077405, lire en ligne, consulté le ).
- ↑ (en) C. K. Ong, Z. G. Song, K. H. Oh et H. Gong, « Variation of the relative permittivity of charged dielectrics », Applied Physics Letters, vol. 72, no 3, , p. 317–319 (ISSN 0003-6951 et 1077-3118, DOI 10.1063/1.120723, lire en ligne, consulté le ).
- 1 2 Yang Minzhong, Liu Shaoyu, Wang Zhuo et Yan Zhang, « Error analysis for dielectric loss factor measurement based on harmonic analysis », Proceedings of 2001 International Symposium on Electrical Insulating Materials (ISEIM 2001). 2001 Asian Conference on Electrical Insulating Diagnosis (ACEID 2001). 33rd Symposium on Electrical and Electronic Insulating Materials and Applications in System, Inst. Electr. Eng. Japan, , p. 336–339 (ISBN 978-4-88686-053-8, DOI 10.1109/ISEIM.2001.973664, lire en ligne, consulté le ).
- ↑ (en) Richard Geyer, Dielectric Characterization and reference materials, Gaithersburg, NIST, (lire en ligne).
- ↑ (en) Robert W. Boyd, « Order-of-magnitude estimates of the nonlinear optical susceptibility », Journal of Modern Optics, vol. 46, no 3, , p. 367–378 (ISSN 0950-0340 et 1362-3044, DOI 10.1080/09500349908231277, lire en ligne, consulté le ).
- ↑ Bube, Richard H., Electrons in solids: an introductory survey, Academic Press, (ISBN 0-12-138553-1 et 978-0-12-138553-8, OCLC 24870700, lire en ligne).
- ↑ (en) D. A. A. S. Narayana Rao, « Ionic polarisation in crystals: Additivity in double salts », Proceedings of the Indian Academy of Sciences - Section A, vol. 30, no 6, , p. 317–319 (ISSN 0370-0089, DOI 10.1007/BF03048749, lire en ligne, consulté le ).
- ↑ (en) Hans J. Liebe, George A. Hufford et Takeshi Manabe, « A model for the complex permittivity of water at frequencies below 1 THz », International Journal of Infrared and Millimeter Waves, vol. 12, no 7, , p. 659–675 (ISSN 0195-9271 et 1572-9559, DOI 10.1007/BF01008897, lire en ligne, consulté le ).
- 1 2 Levy, Elie, Dictionnaire de physique, Presses universitaires de France, (ISBN 2-13-039311-X et 978-2-13-039311-5, OCLC 299407253, lire en ligne).
- ↑ (en) Kwan Chi Kao, « 2 - Electric Polarization and Relaxation », dans Dielectric Phenomena in Solids, Academic Press, (ISBN 978-0-12-396561-5, lire en ligne), p. 41–114
- ↑ (en) W. J. Ellison, « Permittivity of Pure Water, at Standard Atmospheric Pressure, over the Frequency Range 0–25THz and the Temperature Range 0–100°C », Journal of Physical and Chemical Reference Data, vol. 36, no 1, , p. 1–18 (ISSN 0047-2689 et 1529-7845, DOI 10.1063/1.2360986, lire en ligne, consulté le ).
- 1 2 3 4 Jean-Philippe Manceau, Étude du phénomène de relaxation diélectrique dans les capacités Métal-Isolant-Métal, (lire en ligne).
- ↑ (en) Jacob N. Wilson, Jarvist M. Frost, Suzanne K. Wallace et Aron Walsh, « Dielectric and ferroic properties of metal halide perovskites », APL Materials, vol. 7, no 1, , p. 010901 (ISSN 2166-532X, DOI 10.1063/1.5079633, lire en ligne, consulté le ).
- ↑ (en) Ivan Popov, Paul Ben Ishai, Airat Khamzin et Yuri Feldman, « The mechanism of the dielectric relaxation in water », Physical Chemistry Chemical Physics, vol. 18, no 20, , p. 13941–13953 (ISSN 1463-9076 et 1463-9084, DOI 10.1039/C6CP02195F, lire en ligne, consulté le ).
- ↑ Born, Max, Principles of optics: electromagnetic theory of propagation, interference and diffraction of light, Pergamon Press, (ISBN 0-08-026482-4, 0-08-026481-6 et 978-0-08-026481-3, OCLC 7106160, lire en ligne).
- ↑ (en) Karin Wiesauer et Christian Jördens, « Recent Advances in Birefringence Studies at THz Frequencies », Journal of Infrared, Millimeter, and Terahertz Waves, vol. 34, no 11, , p. 663–681 (ISSN 1866-6906, DOI 10.1007/s10762-013-9976-4, lire en ligne, consulté le )
- ↑ (en) « Frustrated Total Internal Reflection », sur sciencedemonstrations.fas.harvard.edu (consulté le )
- ↑ P. Osmokrovic, I. Krivokapic et S. Krstic, « Mechanism of electrical breakdown left of Paschen minimum », IEEE Transactions on Dielectrics and Electrical Insulation, vol. 1, no 1, , p. 77–81 (DOI 10.1109/94.300234, lire en ligne, consulté le ).
- ↑ M F Gendre, M Haverlag et G M W Kroesen, « Optical and electrostatic potential investigations of electrical breakdown phenomena in a low-pressure gas discharge lamp », Journal of Physics D: Applied Physics, vol. 43, no 23, , p. 234004 (ISSN 0022-3727 et 1361-6463, DOI 10.1088/0022-3727/43/23/234004, lire en ligne, consulté le ).
- 1 2 H M Jones et E E Kunhardt, « Development of pulsed dielectric breakdown in liquids », Journal of Physics D: Applied Physics, vol. 28, no 1, , p. 178–188 (ISSN 0022-3727 et 1361-6463, DOI 10.1088/0022-3727/28/1/025, lire en ligne, consulté le )
- 1 2 Vladimir M. Atrazhev, Vladimir S. Vorob'ev, Igor V. Timoshkin et Martin J. Given, « Mechanisms of Impulse Breakdown in Liquid: The Role of Joule Heating and Formation of Gas Cavities », IEEE Transactions on Plasma Science, vol. 38, no 10, , p. 2644–2651 (ISSN 0093-3813 et 1939-9375, DOI 10.1109/TPS.2010.2046337, lire en ligne, consulté le ).
- ↑ Liang Zhao, « Theoretical calculation on formative time lag in polymer breakdown on a nanosecond time scale », IEEE Transactions on Dielectrics and Electrical Insulation, vol. 27, no 4, , p. 1051–1058 (ISSN 1070-9878 et 1558-4135, DOI 10.1109/TDEI.2019.008127, lire en ligne, consulté le ).
- ↑ Brissaud, Michel, Matériaux piézoélectriques : Caractérisation, modélisation et vibration, Presses polytechniques et universitaires romandes, (ISBN 978-2-88074-692-6 et 2-88074-692-2, OCLC 180695932, lire en ligne).
- ↑ (en) Ronald Pethig, « Review Article—Dielectrophoresis: Status of the theory, technology, and applications », Biomicrofluidics, vol. 4, no 2, , p. 022811 (ISSN 1932-1058, PMID 20697589, PMCID PMC2917862, DOI 10.1063/1.3456626, lire en ligne, consulté le ).
- ↑ Jack Arabian, Computer integrated electronics manufacturing and testing, Marcel Dekker, (ISBN 978-1-000-10368-7 et 1-000-10368-4, OCLC 1200290195, lire en ligne), p. 2
- ↑ Agata Skwarek, « Guest editorial », Circuit World, vol. 45, no 1, , p. 1–1 (ISSN 0305-6120 et 0305-6120, DOI 10.1108/cw-02-2019-106, lire en ligne, consulté le ).
- ↑ (en) Yanda Jiang, Mengjun Zhou, Zhonghui Shen et Xin Zhang, « Ferroelectric polymers and their nanocomposites for dielectric energy storage applications », APL Materials, vol. 9, no 2, , p. 020905 (ISSN 2166-532X, DOI 10.1063/5.0039126, lire en ligne, consulté le )
- ↑ T. Oshi, S. Tsukao, T. Ishii et S. Itahashi, « Properties of aged oil impregnated paper power capacitor », Proceedings of the 7th International Conference on Properties and Applications of Dielectric Materials (Cat. No.03CH37417), IEEE, vol. 1, , p. 246–249 (ISBN 978-0-7803-7725-7, DOI 10.1109/ICPADM.2003.1218398, lire en ligne, consulté le ).
- ↑ (en) G. Ghibaudo, R. Clerc, E. Vincent et S. Bruyère, « Gate dielectrics for ultimate CMOS technologies – Limitations and alternative solutions », Comptes Rendus de l'Académie des Sciences - Series IV - Physics, vol. 1, no 7, , p. 911–927 (DOI 10.1016/S1296-2147(00)01085-4, lire en ligne, consulté le ).
- 1 2 (en) M.R. Baklanov et K.P. Mogilnikov, « Non-destructive characterisation of porous low-k dielectric films », Microelectronic Engineering, vol. 64, nos 1-4, , p. 335–349 (DOI 10.1016/S0167-9317(02)00807-9, lire en ligne, consulté le ).
- ↑ (en) S. Kurinchyselvan, A. Hariharan, P. Prabunathan et P. Gomathipriya, « Fluorinated polyimide nanocomposites for low K dielectric applications », Journal of Polymer Research, vol. 26, no 9, , p. 207 (ISSN 1022-9760 et 1572-8935, DOI 10.1007/s10965-019-1852-z, lire en ligne, consulté le ).
- ↑ P.D. Ye, G.D. Wilk, J. Kwo et B. Yang, « GaAs MOSFET with oxide gate dielectric grown by atomic layer deposition », IEEE Electron Device Letters, vol. 24, no 4, , p. 209–211 (ISSN 0741-3106 et 1558-0563, DOI 10.1109/LED.2003.812144, lire en ligne, consulté le ).
- ↑ (en) Turgut Ozturk et Muhammet Tahir Güneşer, « Measurement Methods and Extraction Techniques to Obtain the Dielectric Properties of Materials », dans Electrical and Electronic Properties of Materials, IntechOpen, (ISBN 978-1-78984-929-5, DOI 10.5772/intechopen.80276, lire en ligne).
- 1 2 3 4 5 6 (en) Muhammad Taha Jilani, « A Brief Review of Measuring Techniques for Characterization of Dielectric Materials », International Journal of Information Technology and Electrical Engineering, (ISSN 2306-708X).
- ↑ Kuechler 2005, p. 23
- ↑ (en) C. P. L. Rubinger et L. C. Costa, « Building a resonant cavity for the measurement of microwave dielectric permittivity of high loss materials », Microwave and Optical Technology Letters, vol. 49, no 7, , p. 1687–1690 (DOI 10.1002/mop.22506, lire en ligne, consulté le ).
- ↑ (en) Paul M Meaney, Andrew P Gregory, Neil R Epstein et Keith D Paulsen, « Microwave open-ended coaxial dielectric probe: interpretation of the sensing volume re-visited », BMC Medical Physics, vol. 14, no 1, , p. 3 (ISSN 1756-6649, PMID 25002909, PMCID PMC4083041, DOI 10.1186/1756-6649-14-3, lire en ligne, consulté le ).
- ↑ Alessandra La Gioia, Martin O'Halloran, Adnan Elahi et Emily Porter, « Investigation of histology radius for dielectric characterisation of heterogeneous materials », IEEE Transactions on Dielectrics and Electrical Insulation, vol. 25, no 3, , p. 1064–1079 (ISSN 1070-9878 et 1558-4135, DOI 10.1109/TDEI.2018.006912, lire en ligne, consulté le ).
- ↑ (en) R.J. Galley, M. Trachtenberg, A. Langlois et D.G. Barber, « Observations of geophysical and dielectric properties and ground penetrating radar signatures for discrimination of snow, sea ice and freshwater ice thickness », Cold Regions Science and Technology, vol. 57, no 1, , p. 29–38 (DOI 10.1016/j.coldregions.2009.01.003, lire en ligne, consulté le ).
- ↑ (en) Wenke Zhao, Emanuele Forte, Michele Pipan et Gang Tian, « Ground Penetrating Radar (GPR) attribute analysis for archaeological prospection », Journal of Applied Geophysics, vol. 97, , p. 107–117 (DOI 10.1016/j.jappgeo.2013.04.010, lire en ligne, consulté le ).
- ↑ (en) John H. Bradford, Esther L. Babcock, Hans-Peter Marshall et David F. Dickins, « Targeted reflection-waveform inversion of experimental ground-penetrating radar data for quantification of oil spills under sea ice », GEOPHYSICS, vol. 81, no 1, , WA59–WA70 (ISSN 0016-8033 et 1942-2156, DOI 10.1190/geo2015-0170.1, lire en ligne, consulté le ).
Voir aussi
Articles connexes
- Conducteurs d’électricité
- Tension de claquage
Bibliographie
- (de) Andreas Kuechler, Hochspannungstechnik, Grundlagen, Technologie, Anwendungen, Berlin, Springer, , 543 p. (ISBN 3-540-21411-9, lire en ligne).















































