أشكال الطاقة

عندما تكتسب المادة حرارة ترتفع طاقة الحركة لجزيئاتها وتظهر في صورة طاقة حرارية و يمكن تحويل الطاقة الحرارية إلى أي نوع آخر من الطاقة مثل الطاقة الميكانيكية كما في السيارة ، أو طاقة كهربائية كما في محطة الطاقة الكهربائية أو طاقة إشعاعية كما في النار أو في النجوم وغيرها.

في العلوم الفيزيائية توجد العديد من أشكال الطاقة مثل :

هذة القائمة غير كاملة فيوجد أشكال عديدة من الطاقة لم يتم ذكرها، فكلما إكتشف علماء الفيزياء ظاهرة تحقق قانون بقاء الطاقة يتم دراستة واعتبارها شكل من أشكال الطاقة .

الحرارة والشّغل هي أشكال خاصة من أشكال الطاقة فهي ليست من خصائص النظام ولكنها تعتبر من حالات نقل الطاقة . فبشكل عام لا يمكن قياس مقدار الحرارة أو الشغل الموجود في كائن ما . وإنما يتم قياس مقدار الطاقة التي يمكن نقلها بين الأجسام بطرق معينة أثناء وقوع عملية معينة . ويتم إضافة إشارة موجب أو سالب أثناء قياس كل من الحرارة والشّغل كإشارة على اتجاه انتقال الحرارة أو أن الجسم قد قام بشغل أم تعرض له .

وتهتم الميكانيكا الكلاسيكية بتوضيح الفرق بين الطاقة الحركية وهي الطاقة التي يمتلكها الجسم بسبب حركتة وتساوي الشغل اللازم لتسريع جسم ما من حالة السكون إلى سرعة معُينة، سواء كانت سرعة مستقيمة أو زاوية , وطاقة الوضع و تسمي أيضا طاقة الارتفاع وهي طاقة كامنة يكتسبها الجسم بسبب وقوعه تحت تأثير جاذبية مثل الجاذبية الأرضية أو تحت تأثير مجال كهربائي إذا كان له شحنة كهربائية أو تحت تأثير قوة شد مرنة مثل الزنبرك , وتتغير طاقة وضع الجسم بتغير ارتفاعه عن سطح الأرض . والطاقة النووية بأنواعها كالقوة النووية والقوة النووية الضعيفة . والطاقة الكهربية والتي تحدث نتيجة تعرض الجسم للمجالات الكهربية . والطاقة المغناطيسية والتي تحدث نتيجة تعرض جسم ما لمجال مغناطيسي .

بينما توجد أنواع آخري من الطاقة عبارة عن مزيج بين طاقة الحركة وطاقة الوضع مثل الطاقة الميكانيكية وهي عبارة عن المقياس العيانى لمجموع طاقة الحركة وطاقة الوضع .
وطاقة الوضع المرنة والتي تعتمد على الطاقة الكهربائية الكامنة (بين الذرات والجزيئات) , وتعتمد أيضا على الطاقة الكيميائية .

وعند قياس الطاقة يجب ذكر إذا كانت موجبة أو سالبة بمقارنتها بقيمتها في حالة معينة، فمثلا طاقة الموجة الميكانيكية ( موجة الضوء أو موجة الصوت ) , وطاقة الحركة , و طاقة الكتلة الساكنة دائما ما تكون أكبر من أو تساوي الصفر، لأنها يتم مقارنتها مع حالة المادة في وضع السكون والتي تكون طاقة الحركة فيها تساوي صفر .

وقد تم تصنيف جميع أشكال الطاقة على أنها إما طاقة حركة أو طاقة وضع , ولكن الفيزيائي الأمريكي ريتشارد فاينمان الحاصل على جائزة نوبل عام 1965 أشار قائلا " إن هذة المفاهيم عن طاقة الحركة وطاقة الوضع تعتمد على مفهوم المقياس العياني " .

ويمكن أن تتحول الطاقة من صورة إلى صورة آخرى بكفاءات تحويل مختلفة . وتسمى المواد التي تحول الطاقة من شكل إلى أخر بالمبدلات .

الطاقة الميكانيكية

الميكانيكا العامة غير النسبية

تتواجد الطاقة الميكانيكية ( ورمزها هو E_M أو E ) بصور مختلفة . ولكن يمكن تصنفيها كنوع من أنواع طاقة الوضع ( E_p, V, U , Φ) أو طاقة الحركة (E_k , T) . ويعتبر مصطلح طاقة الوضع مصطلح عام جدا فهو يستخدم مع جميع مجالات القوى مثل الجاذبية , المجالات الكهربية , المجالات المغناطيسية , فهي تشير إلى الطاقة التي يكتسبها الجسم نتيجة تواجده في مجال ما .

والعلاقة بين الطاقة الميكانيكية وطاقة الوضع والحركة هي :

${\displaystyle E=T+V\,\!}$.

ميكانيكا لاجرانج و هاملتوني

وفي مواضيع أكثر تقدما، يعتبر مجموع كلا من طاقة لحركة وطاقة الوضع هي الطاقة الكلية لنظام ما وتعرف بمعادلة هاميلتون :

${\displaystyle H=T+V,\,\!}$

وتعتبر ميكانيكا لاجرانج وهاملتوني هي إعادة صياغة للميكانيكا الكلاسيكية وتستخدم للحصول على المعادلات التي تصف النظام الكلاسيكي بالطاقة بدلا من القوة . فتكون المعادلة بالشكل التالي :

${\displaystyle L=T-V\,\!}$,

طاقة الحركة

نظرة عامة

حركة البندول تعتبر من أفضل الأمثلة عند دراسة طاقة الحركة وطاقة الوضع

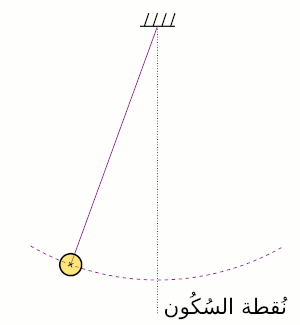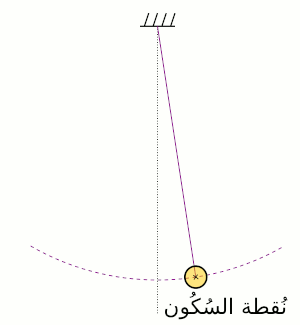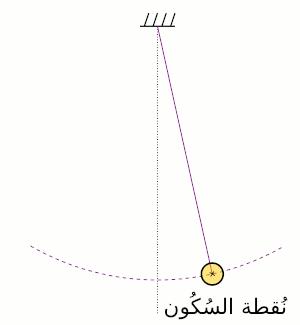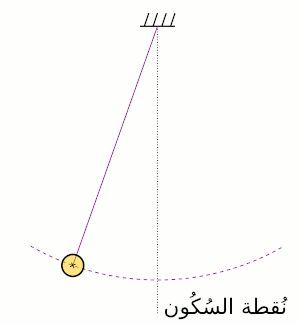
هي الطاقة التي يمتلكها الجسم بسبب حركته . هي تُساوي الشغل اللازم لتسريع جسم ما من حالة السكون إلى سرعة معُينة، سواء كانت سرعة مستقيمة أو زاويّة . وتساوي :

${\displaystyle E_{\mathrm {k} }=\int \mathbf {F} \cdot d\mathbf {x} =\int \mathbf {v} \cdot d\mathbf {p} }$

الميكانيكا الكلاسيكية

في الميكانيكا الكلاسيكية، لأي كتلة m فإن القوة F المؤثرة عليها تساوي F = ma حيث a هي العجلة . وتكون العلاقة بالشكل التالي :

${\displaystyle E_{\mathrm {k} }=\int \mathbf {F} \cdot d\mathbf {x} =m\int {\frac {d\mathbf {v} }{dt}}\cdot \mathbf {v} dt=m\int d\mathbf {v} \cdot \mathbf {v} =m\int {\frac {1}{2}}d(\mathbf {v} \cdot \mathbf {v} )={\frac {1}{2}}mv^{2}\,\!}$

الميكانيكا النسبية الخاصة

عندما تقترب سرعة الجسم v من سرعة الضوء c , يجب حساب الشغل المبذول بإستخدام تحويلات لورينتز لتكون المعادلة بالشكل التالي :

${\displaystyle E_{\mathrm {k} }=\left(\gamma -1\right)mc^{2},}$

حيث

${\displaystyle \gamma ={\frac {1}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}}$

ويسمي معامل لورنتز , ويمكن كتابتة بالشكل التالي :

${\displaystyle \gamma \equiv {\frac {c}{\sqrt {c^{2}-v^{2}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}}$

حيث:

${\displaystyle \beta ={\frac {v}{c}}}$ مقسوم السرعة النسبية على سرعة الضوء,

v السرعة النسبية

c هي سرعة الضوء.

وتكون طاقة الحركة مساوية للصفر عندما عندما تكون السرعة تساوي صفر (v=0) فتكون جاما تساوي 1 (γ= 1) لتكون العلاقة بالشكل التالي :

${\displaystyle E_{0}=m_{0}c^{2}\,\!}$

إشتقاق القانون

الشغل المبذول على جسم بواسطة القوة F خلال جزء زمني صغير dt فيتحرك مسافة dx، يعادل حاصل الضرب المقياسي للقوة والإزاحة :

${\displaystyle \mathbf {F} \cdot d\mathbf {x} =\mathbf {F} \cdot \mathbf {v} dt={\frac {d\mathbf {p} }{dt}}\cdot \mathbf {v} dt=\mathbf {v} \cdot d\mathbf {p} =\mathbf {v} \cdot d(m\mathbf {v} )}$

${\displaystyle d(\mathbf {v} \cdot \mathbf {v} )=(d\mathbf {v} )\cdot \mathbf {v} +\mathbf {v} \cdot (d\mathbf {v} )=2(\mathbf {v} \cdot d\mathbf {v} )}$

وبفرض ثبات الكتلة :

${\displaystyle \mathbf {v} \cdot d(m\mathbf {v} )={\frac {m}{2}}d(\mathbf {v} \cdot \mathbf {v} )={\frac {m}{2}}dv^{2}=d\left({\frac {mv^{2}}{2}}\right)}$

${\displaystyle E_{k}=\int \mathbf {F} \cdot d\mathbf {x} =\int \mathbf {v} \cdot d\mathbf {p} ={\frac {mv^{2}}{2}}}$

طاقة الوضع

طاقة الوضع هي الطاقة التي يمتلكها الجسم بسبب وضعه أو حالته، أو نتيجة وقوعه تحت تأثير جاذبية مثل الجاذبية الأرضية , أو مجال ما مثل المجال المغناطيسي أو المجال الكهربي إذا كان له شحنة كهربائية .أو تحت تأثير قوة شد مرنة مثل الزنبرك . وتتغير طاقة وضع الجسم بتغير ارتفاعه عن سطح الأرض الذي يشكل مرجعا لحساب تلك الطاقة .

ويتم تعريف طاقة الوضع على أنها الشغل المبذول على جسم ما لتكون المعادلة بالشكل التالي :

${\displaystyle \Delta U=-\Delta W}$.

الشغل الميكانيكي

يعرف الشغل على أنه كمية الطاقة اللازمة لتحريك جسم ما بقوة ما لمسافة ما، فإذا كانت القوة F والإزاحة r فإن الشغل المبذول لنقل الجسم من r₁ إلى r₂ يأتي من العلاقة التالية :

${\displaystyle \Delta W=\int _{\mathbf {r} _{1}}^{\mathbf {r} _{2}}\mathbf {F} \cdot \mathrm {d} \mathbf {r} }$,

بحيث يكون الضرب هو ضرب قياسي للمتجهين . ويمكن تبسيط المعادلة السابقة في حالات معينة مثل التعامل مع الجاذبية الأرضية أو مع طاقة الوضع المرنة لتكون المعادلة بالشكل التالي :

${\displaystyle \mathbf {F} =\nabla W}$.

الحركة الدورانية

هي حركة التفاف حول مركز الجسم نفسه، وهو الشغل الي يبذلة العزم τ بين الزاويتين θ₁ و θ₂ ويساوي :

${\displaystyle \Delta W=\int _{\theta _{1}}^{\theta _{2}}\left|{\boldsymbol {\tau }}\right|\mathrm {d} \theta }$.

طاقة الوضع المرنة

سقوط كرة تحت تأثير الجاذبية الأرضية وتغير كل من طاقة وضعها وطاقة حركتها

طاقة الوضع المرنة هي طاقة الوضع التي يحتملها الجسم المادي المرن عند تغيير وضعه في الأصل بضغطه أو تمديده . وقوة الشد أو الضغط F على زنبرك تتبع قانون هوك الذي يشير إلى أن الكمية التي يتغير بها الجسم (الإجهاد) مرتبطة خطيًا بالقوة المسببة لهذا التغير (الشد / الضغط ) .

${\displaystyle \mathbf {F} =k\mathbf {x} \ }$

حيث :

${\displaystyle \ \mathbf {x} }$ هي الفرق في المسافة بين موضع الجسم الجديد وموقعه الأصلي سواء كان مضغوطًا أو ممدودًا "الإزاحة الحاصلة" (عادة تقاس بالمتر) .

${\displaystyle \ \mathbf {F} }$ هي قوة الإعادة أو كما يطلق عليها القوة المشوهة للجسم أي معناها أن هذه القوة تغير من أبعاد الجسم ولو وصلت لحد معين قد تسبب تشوه للجسم أي لا يعود لشكله الأصلي قبل أن تؤثر عليه تلك القوة التي تمارسها المادة (عادة تقاس بالنيوتن) .

${\displaystyle \ \mathbf {k} }$هو ثابت القوة ووحدته القوة إلى الطول (يقاس بالنيوتن لكل متر) .

ويحسب الشغل من العلاقة التالية :

${\displaystyle E_{\mathrm {p,e} }={\frac {1}{2}}kx^{2}\,\!}$.

طاقة السطح

سبب تكون التوتر السطحي هو أن القوى والروابط بين جزيئات السائل هي المسؤلة عن التوتر السطحي والجزيئات على السطح ليس لديها جزيئات فوقها لذلك تكون قوى الترابط على الجزيئات الأخرى المحيطة بها أقوى مقارنة بالجزيئات الداخلية

يرمز للتوتر السطحي بالرمز σ, γ أو T، ويعرّف بأنه القوة المؤثرة عموديّا على طول خط عمل وحدة القوى عندما تكون هذه القوة موازية للسطح. ويقاس التوتر السطحي بوحدات نيوتن لكل متر(N·m⁻¹)، أو داين لكل سنتيميتر. وبالنسبة للديناميكا الحرارية يعرف التوتر السطحي على أنه الشغل المبذول لوحدة المساحات .

أمثلة على التوتر السطحي في حياتنا اليومية

قطرات الماء تأخذ أشكالاً شبه كروية

• تقدم ظاهرة الشد السطحي تفسيراً لكثير من الظواهر الشائعة في حياتنا . فعلى سبيل المثال تأخذ قطرات السوائل أشكال شبه كروية بسبب ظاهرة الشد السطحي .
• وتقدم ظاهرة التوتر السطحي تفسيراً لإمكانية عمل فقاعات الصابون بينما لا يمكن القيام بعمل فقاعات باستخدام الماء النقي وحده .
• كما أن إضافة الصابون إلى الماء تجعله منظفاً ممتازاً عبر تقليل توتره السطحي وبالتالي تجعله قادراً على تبليل والإحاطة بالأوساخ لتسهل إزالتها .

تقيس طاقة السطح مدى تحطم الروابط بين الجزيئية الذي يحدث عند تشكل سطح ما، أو تقطيع جسم صلب إلى قطع صغيرة .

إذا كانت γ هو التوتر السطحي , S هي مساحة السطح، فإن الشغل المبذول W لزيادة مساحة السطح تأتي من العلاقة التالية :

${\displaystyle \mathrm {d} W=\gamma \mathrm {d} S.\,\!}$

طاقة الصوت

الصوت هو شكل من أشكال الاهتزازات الميكانيكية التي تنتشر من خلال أي وسط مادي . ويرتبط ارتباطا وثيقا بقدرة الأذن البشرية على إدراك الصوت . ويعمل الجزء الخارجي من الأذن إلى جمع وتكبير الاهتزازات الصوتية . ليضرب طبلة الأذن لتترجم الاهتزازات إلى صوت تسمعه الأذن الداخلية .

ويتم قياس الطاقة الصوتية من المعادلة التالية :

${\displaystyle W=W_{\mathrm {pot} }+W_{\mathrm {kin} }=\int _{V}{\frac {p^{2}}{2\rho _{0}c^{2}}}dV+\int _{V}{\frac {\rho v^{2}}{2}}dV}$

حيث

${\displaystyle p}$ ضغط الصوت .
${\displaystyle v}$ سرعة الجسيمات .
${\displaystyle \rho _{0}}$ الكثافة .
${\displaystyle c}$ سرعة الصوت .

طاقة الوضع الجاذبية

طاقة الوضع الجاذبية هي شكل من أشكال الطاقة المتعلقة بالجاذبية . فإذا إفترضنا وجود جسم كتلته m وعلى إرتفاع رأسي من الأرض يساوي h وتحت تأثير عجلة الجاذبية الأرضية g وقيمتها g = 9.81 m s⁻¹ . وتكون المعادلة كالتالي :

${\displaystyle E_{\mathrm {p,g} }\approx mgh\,\!}$

وعند وجود كتلتين m₁ و m₂ فإن العلاقة تتبع قانون الجذب العام لنيوتن وتكون بالشكل التالي :

${\displaystyle E_{\mathrm {p,g} }=-{\frac {Gm_{1}m_{2}}{r}}\,\!}$,

حيث

r هي المسافة بين الكتلتين .

G هو ثابت الجاذبية ويساوي ^[1]

${\displaystyle G=\left(6.67428\pm 0.00067\right)\times 10^{-11}\ {\mbox{m}}^{3}\ {\mbox{kg}}^{-1}\ {\mbox{s}}^{-2}.}$

وفي هذة الحالة يجب الحرص على أن تكون النقطتين كروية الشكل أو منتظمة الشكل، فلا يمكن تطبيقها على أي جسم ولا على أي كتلة .

ويمكن كتابة المعادلة بصيغة آخرى بدلالة (Φ, U, V) وتكون كالتالي :

${\displaystyle E_{\mathrm {p,g} }=-\Phi m\,\!}$.

الطاقة الحرارية

نظرة عامة

الطاقة الحرارية هي شكل معهود من أشكال الطاقة، يتم انتقالها عن طريق التوصيل أو الإشعاع أو الحمل . حيث يتم انتقال الحرارة دائما من الجسم الساخن إلى البارد. ويتسبب انتقال الحرارة من جسم إلى جسم إلى رفع درجة حرارته . يمكن تحويل الطاقة الحرارية إلى أي نوع آخر من الطاقة مثل الطاقة الميكانيكية كما في السيارة ، أو طاقة كهربائية كما في محطة الطاقة الكهربائية أو طاقة إشعاعية كما في النار أو في النجوم وغيرها، كما أننا نستغلها في إدارة المحركات مثل الآلة البخارية ومحرك الاحتراق الداخلي والمحرك النفاث والصواريخ .

لهذا حظيت الطاقة الحرارية منذ القدم بالدراسة، وصيغت قوانينها خلال القرن التاسع عشر فيما يسمى علم الحركة الحرارية (ترموديناميكا).

تعرف الطاقة الحرارية E_th لمادة بالمعادلة :

${\displaystyle E_{th}=c\;\cdot m\;\cdot T\!}$

حيث:

c الحرارة النوعية,

m الكتلة

T درجة الحرارة المطلقة ، كلفن.

عند خلط نظامين مختلفين في درجة الحرارة ,فإن الحرارة تنتقل من النظام الساخن إلى النظام البارد . ويستمر انتقال الحرارة بينهما حتى تتساوى درجة الحرارة ويصبح النظام الكلي في حالة توازن حراري , وتلك العملية تسمى انتقال الحرارة . وهذا التوازن يحدث تلقائيا، ولا يمكن انتقال حرارة من جسم بارد إلى جسم ساخن . وتلك الظاهرة المعروفة معرفة في القانون الثاني للديناميكا الحرارية ، وهو أحد قوانين الترموديناميكا .

وتكون المعادلة بالشكل التالي :

${\displaystyle \Delta q=\int _{T_{1}}^{T_{2}}C_{\mathrm {v} }\mathrm {d} T}$

الطاقة الحركية

حركة حرارية لجزء من جزيئ بروتين.

عندما تكتسب المادة حرارة ترتفع طاقة الحركة لجزيئاتها وتظهر في صورة طاقة حرارية ، ويسبب انخفاض الحرارة لجسم ما من طاقة حركة جزيئاته. فالطاقة الحرارية هي طاقة حركية وتلك الحركة تظهر كحركة عشوائية لجزيئات المادة في الغازات والسوائل، وحركة اهتزازية للشبكة البلورية للمادة الصلبة وينقلها ما يسمى فوتون.

إذا كانت الطاقة الحركية لجميع جزيئات مادة ما مساوية للصفر، فتكون درجة حرارته عند الصفر المطلق حيث الكتلة m والحرارة النوعية c دائما لا تصلان إلى الصفر . ومقياس درجة الحرارة هي كلفن وهي المرجع لمقاييس درجة الحرارة مثل الدرجة المئوية أو الدرجة الفاهرنهيتية . درجة الصفر المطلق هي -16 و273 بدرجة الحرارة المئوية .

وفي النظرية الحركية للغازات فإن درجة الحرية للغاز المثالي تأتي من العلاقة التالية :

${\displaystyle U={\frac {d_{f}}{2}}k_{B}T}$

حيث

d_f هي درجة الحرية .
k_B هو ثابت بولتزمان وهو يعطي متوسط طاقة الحركة لكل جزيء أو ذرة في الغاز بمجرد معرفة درجة الحرارة المطلقة للغاز. وهو عبارة عن حاصل قسمة ثابت الغازاتR على عدد أفوجادرو (N_A) :

${\displaystyle k={\frac {R}{N_{\rm {A}}}}.\,}$

علم الحركة الحرارية الكيميائية

الطاقة الكيميائية هي الطاقة التي تحدث نتيجة التفاعلات بين الجزيئات . وويمكن تعريفها بأنه الشغل التي تبذلة القوة الكهربية خلال إعادة ترتيب الشحنات الكهربائية , الإلكترونات , البروتونات . وإذا إنخفضت الطاقة الكيميائية لنظام ما خلال تفاعل كيميائي يظهر الفقد في صورة حرارة أو ضوء . والعكس صحيح إذا زادت الطاقة الكيميائية لنظام ما خلال تفاعل كيميائي يكون سبب هذة الزياده تعرض النظام لحرارة أو ضوء . كما يلي :

• عند تفاعل ذرتين من ذرات الهيدروجين لتكوين جزئ الهيدروجين، تنخفض الطاقة الكيميائية بمقدار 724 zj والتي تستهلك في ربط الذرات مع بعضها والمسمى العلمي لها هو طاقة الرابطة .
• عند إزالة إلكترون تماما من ذرة الهيدروجين , تزداد الطاقة الكيميائية بمقدار 2.18 aj وهي ما تسببها طاقة التأين .

قد تظهر أحيانا كحرارة ناتجة عن التفاعل الكيميائي . وهي أيضا الحرارة الناتجة عن الاحتراق حيث يتحد كربون مع الأكسجين وتنشأ منه حرارة ونارا . كما نستغل التفاعل بين الكيروسين و الأكسجين في محرك الاحتراق الداخلي لإنتاج حركة السيارة . ويمكننا بواسطة قانون هس حساب الطاقة الناتجة عن طريق قيم الإنثالبي القياسي للتكوين للمواد المشتركة في التفاعل .

علم الحركة الحرارية الكيميائية هو أحد فروع علم الحركة الحرارية (الترموديناميكا) التي تهتم بدراسة الحركة الحرارية في الأجسام والأنظمة . وتتعلق الترمودينامكا الكيميائية بدراسة علاقة الحرارة و الشغل بالتفاعلات الكيميائية أو علاقتهما بالتغيرات الفيزيائية لحالة نظام يتبع قوانين الترموديناميكا. وتتضمن الترمودینامیكا الكيميائية القياس المعملي للعمليات المختلفة وكذلك تطبيق الطرق الرياضية في دراسة مسألة التفاعلات والتغير الطبيعي التلقائي الذي يحدث في عمليات مختلفة .

وقد أشار بعض الكيميائين إلى الطاقة الكيميائية على أنها نوع من أنواع الطاقة الداخلية U ويمكن قياسها عند ثبات حجم النظام . ولكن عند تغير الحجم وثبات الضغط ( كما في حالة الغازات ) , يجب إعادة الحسابات مرة أخرى لمعرفة المحتوى الحراري للنظام H (الإنثالبي ) .
ويعتبر التغير في الإنثالبي ΔH لنظام ما هو الشغل غير الميكانيكي الذي نمد به النظام أو كمية الحرارة التي نعطيها لنظام ما . وبهذة الحسابات نستطيع معرفة الشغل الذي يمكن الاستفادة منه من النظام (عند الاحتفاظ بالضغط ثابتا). { ذلك لأنه عند ثبات الضغط يتغير الحجم، وتغير حجم النظام معناه أن النظام يؤدي شغلا ميكانيكيا ويعطيه إلى الوسط المحيط. كمية الشغل p. V } .

${\displaystyle \Delta E=p\Delta V\,\!}$,

وتكون معادلة الإنثالبي كالتالي :

${\displaystyle \Delta H=\Delta U+p\Delta V\,\!}$.

والتصحيح الثاني في المعادلة هو الإنتروبيا , لمعرفة مدى إمكانية التفاعل بين النظام الوسط المحيط ^[2].

بعد إزالة الحائل يشغل الغاز الحجم بالكامل . وبذلك تزيد إنتروبية النظام (تجربة جاي لوزاك).

${\displaystyle \Delta E=T\Delta S\,\!}$,

مع مراعاه طاقة غيبس الحرة والتي تعتمد على المتغيرات الطبيعية المستقلة مثل درجة الحرارة T والضغط p و كمية المادة n ، يرمز له عادة بالرمز G . وتكون معادلتها بالشكل التالي :

${\displaystyle G\;=\;U\;+\;p\cdot V\;-\;T\cdot S}$ حيث:

U الطاقة الداخلية لنظام ترموديناميكي،

V الحجم،

p الضغط ،

S الإنتروبي

T درجة الحرارة

وتكتب معادلة جيبس للطاقة الحرة أيضا بطريقة أخرى:

${\displaystyle G\;=\;H-\;T\cdot S}$

حيث H الطاقة الكلية للنظام وتسمى أيضا هاملتوني وترجع تسميتها إلى عالم الفيزياء هاملتون .

${\displaystyle \Delta G=\Delta H-T\Delta S\,\!}$.

هذة التصحيحات يتم إهمالها في أغلب الحالات إلا عند التعامل مع الغازات .

ومنذ الثورة الصناعية , واستخدام فكرة تحويل الطاقة من صورة إلى صورة آخرى في الصناعة وتوليد الطاقة مثل حرق الفحم , الوقود , الغاز الطبيعي وأنواع أخرى كثيرة من الوقود الحفري :

• 1 طن مكافئ من الفحم (TCE) يولد 29.3076 GJ والتي تعادل 8141 كيلوواط ساعي .
• 1 طن نفط مكافئ (TOE) يولد 41.868 GJ والتي تعادل 11630 كيلوواط ساعي .

وطبقا لنموذج بور للذرات، فإن الطاقة الكيميائية مرتبطة بثابت ريدبرغ .

${\displaystyle R_{y}={\frac {m_{e}e^{4}}{8\varepsilon _{0}^{2}h^{2}}}={\frac {1}{2}}\alpha ^{2}m_{e}c^{2}=13.605\;692\;53(30)\ \mathrm {eV} }$

الطاقة الكهربية

الطاقة الكهروستاتيكية

نظرة عامة

طاقة الوضع الكهربائية لجسيم نقطي q في وجود n جسيم نقطي Q₂ charge system:${\displaystyle U_{E}=q{\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {Q_{1}}{r_{1}}}+{\frac {Q_{2}}{r_{2}}}\right)}$

تعرف طاقة الوضع الكهربائية لنقطة ما بأنها الشغل المبذول في تحريك وحدة الشحنات الكهربائية من اللانهاية إلى تلك النقطة (دون إحداث أي تغيير في الطاقة الحركية لها ) . بشرط اختيار نقطة مرجعية يكون الجهد عندها يساوي صفراً . فإذا كانت هناك شحنتان Q₁ و Q₂ المسافة بينهما r فإن طاقة الوضع الكهربائية تأتي من العلاقة التالية :

${\displaystyle E_{\mathrm {p,e} }={\frac {1}{4\pi \epsilon _{0}}}{{Q_{1}Q_{2}} \over {r}}}$

حيث

ε₀ هي سماحية الفراغ الكهربائية ^[3]. وتساوي

${\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c_{0}^{2}}}}$

= 8.854...×10⁻¹² أمبير ·ثانية/(فولت·متر) = 8.854 ...×10⁻¹² فاراد/متر

حيث :

c₀ سرعة الضوء في الفراغ .
μ₀ نفاذية الفراغ المغناطيسية .

ويمكن كتابتها بدلالة ϕ لتكون بالشكل التالي :

${\displaystyle E_{\mathrm {p,e} }=\phi q\,\!}$.

إذا تراكمت هذة الشحنة داخل مكثف ذو سعة كهربية C تكون المعادلة فيهذة الحالة على النحو التالي :

${\displaystyle E_{\mathrm {p,e} }={\frac {Q^{2}}{2C}}={\frac {1}{2}}CV^{2}={\frac {1}{2}}VQ\,\!}$,

الطاقة الكهربية

الدوائر الكهربية

دائرة كهربائية بسيطة مكونة من مصدر جهد ومقاومة كهربية وطبقا لقانون أوم فإن الجهد يساوي ${\displaystyle V=iR}$ .

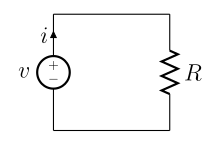
إذا مر تيار كهربي في مقاومة , تتحول الطاقة الكهربية إلى حرارة , وعند مرور التيار الكهربي على الأجهزة الكهربية فسيتحول هذا التيار إلى أشكال عديدة من الطاقة كطاقة حركية على سبيل المثال ( مع الأخذ في الاعتبار ان جزء بسيط من التيار سيفقد على شكل حرارة أيضا وهذا الجزء يعتمد على كفاءة الجهاز ) . والمعادلة التي تربط بين الطاقة والجهد والتيار لها أشكال عديدة منها :

${\displaystyle E=VQ=VIt=Pt={\frac {V^{2}t}{R}}={I^{2}}Rt\,\!}$

حيث

V هو فرق الجهد ويقاس بالفولت .
Q هي الشحنة الكهربائية وتقاس بالكولوم .
I هو التيار الكهربي ويقاس بالأمبير .
t الزمن وتقاس بالثانية .
P هي القدرة وتقاس بالواط .
R هي المقاومة الكهربية وتقاس بالأوم .

الطاقة المغناطيسية

لا يوجد فرق جوهري بين الطاقة الكهربية والطاقة المغناطيسية، فهما مرتبطان بمعادلات ماكسويل التي تنص على

" إذا انتقلت دائرة أو جزء من دائرة كهربائية مغلقة ضمن مجال مغناطيسي منتظم فإنها تبذل شغلاً يساوي شدة التيار الكهربائي المارة فيها في تغير التدفق المغناطيسي الذي يجتازها "

والطاقة الكهربية لعزم مغناطيسي m يقع داخل حقل مغناطيسي B يساوي :

${\displaystyle E_{\mathrm {p,m} }=-\mathbf {m} \cdot \mathbf {B} }$.

ملف كهربي

الدوائر الكهربية

الطاقة التي يخزنها ملف محادثته التبادلية L يمر به تيار I تساوي :

${\displaystyle E_{\mathrm {p,m} }={\frac {1}{2}}LI^{2}}$.

الطاقة الكهرومغناطيسية

لحساب الشغل المبذول يجب إنشاء حقل كهربي أو مغناطيسي في وحدة الحجوم ( مكثفات , ملفات ) وحساب كثافة الطاقة

${\displaystyle u_{e}={\frac {\epsilon _{0}}{2}}\left|\mathbf {E} \right|^{2},\quad u_{m}={\frac {1}{2\mu _{0}}}\left|\mathbf {B} \right|^{2}\,\!}$,

بشرط أن تكون الوحدات على ( نظام الوحدات الدولي )

الإشعاع الكهرومغناطيسي مثل أشعة ميكروويف , الضوء المرئي , وأشعة غاما هي عبارة عن تدفق للطاقة الكهرومغناطيسية . ويتم التعبير عن متجه بوينتنج الخاص بهم بواسطة المعادلة التالية :

${\displaystyle \mathbf {S} ={\frac {1}{\mu }}\mathbf {E} \times \mathbf {B} ,}$

وتكون طاقة الفوتون

${\displaystyle E=h\nu ={\frac {hc}{\lambda }}\,\!}$,

ليكون التباعد بين مستويات الطاقة

${\displaystyle \Delta E=E_{2}-E_{1}=hc\left(\nu _{2}-\nu _{1}\right)=hc\left({\frac {1}{\lambda _{2}}}-{\frac {1}{\lambda _{1}}}\right)\,\!}$,

حيث

h هو ثابت بلانك ^[4] وقيمتة
${\displaystyle h=6.626\ 070\times 10^{-34}\ {\mbox{J}}\cdot {\mbox{s}}}$

v هو تردد الإشعاع .

الطاقة النووية

تمد الطاقة النووية و طاقة الوضع الكهربائية الطاقة اللازمة لحدوث الإنشطار النووي و هو عملية انقسام نواة ذرة ثقيلة إلى قسمين أو أكثر، وبهذه العملية يتحول عنصر معين إلى عنصر أخر وينتج عن عملية الانشطار نيوترونات وفوتونات عالية الطاقة (بالأخص أشعة غاما) وجسيمات نووية مثل جسيمات ألفا وأشعة بيتا . ويؤدي انشطار العناصر الثقيلة إلى تولد كميات ضخمة من الطاقة الحرارية والإشعاعية.

وتسبب الطاقة النووية وطاقة الوضع الكهربائية أيضا حدوث الإندماج النووي والذي يعتبر من أحد أهم أنواع التفاعلات النووية التطبيقية . حيث ينطلق خلال هذا الاندماج كمية هائلة من الطاقة تظهر على شكل حرارة وإشعاع كما يحدث في الشمس، فتمدنا بالحرارة والنور والحياة. فبدون هذا التفاعل ما وُجدت الشمس وما وُجدت النجوم، ولا حياة من دون تلك الطاقة المسماة طاقة الاندماج النووي. وتنتج تلك الطاقة الهائلة عن فقد في وزن النواة الناتجة عن الاندماج النووي، وهذا الفقد في الكتلة يتحول إلى طاقة طبقاً لمعادلة ألبرت أينشتاين التي تربط العلاقة بين الكتلة والطاقة .

وتوفر القوة النووية الضعيفة ^[5] ( مختلفة عن القوة القوية ) الطاقة اللازمة لأنواع معينة من التحلل الإشعاعي، مثل تحلل بيتا . وتتفرد القوة النووية الضعيفة بأنها تسمح للكواركات (التي تشكل الجسيمات المركبة مثل البروتونات والنيوترونات على شكل ست نكهات : علوي، وسفلي، وغريب، وساحر، وقمّي، وقعري) في تغيير نكهاتها من نكهة إلى أخرى، فمثلاً يتحول كوارك سفلي إلى آخر علوي أثناء اضمحلال بيتا ليُصبح بذلك النيوترون بروتوناً.
وبالإضافة إلى ذلك فإنّ القوة النووية الضعيفة هي القوة الوحيدة بين القوى الأساسية التي تخرق التكافؤ وكذلك الوحيدة التي تستطيع خرق تناظر الشحنة السوية .

مقالات ذات صلة

• الطاقة
• تخزين الطاقة
• كثافة الطاقة
• الطاقة المتجددة
• الطاقة البحرية
• نقل القدرة
• معهد أبحاث الطاقة الكهربائية
• نمو الخلايا الشمسية

المصادر

موسوعات ذات صلة :

• موسوعة الفيزياء
• موسوعة طاقة
• موسوعة زراعة
• موسوعة علم البيئة
• موسوعة علوم
• موسوعة ماء